Abstract
Review Article
Magnetohydrodynamic CNTs Casson Nanofluid and Radiative heat transfer in a Rotating Channels
Zahir Shah*, Abdullah Dawar, Saeed Islam, Muhammad Idress and Waris Khan
Published: 17 August, 2018 | Volume 1 - Issue 1 | Pages: 017-032
The main purpose of this investigation is to inspect the innovative conception of the magneto hydrodynamic (MHD) nanoparticles of single wall carbon nanotubes base on the fluids (water, engine oil, and ethylene, glycol and kerosene oil) between two rotating parallel plates. Carbon nanotubes (CNTs) parade sole assets due to their rare structure. Such structure has significant optical and electronics features, wonderful strength and elasticity, and high thermal and chemical permanence. The heat exchange phenomena is deliberated subject to thermal radiation. Kerosene oil is taken as based nano fluids because of its unique attention due to their advanced thermal conductivities, exclusive features, and applications. The fluid flow is presumed in steady state. With the help of suitable resemblance variables, the fundamental leading equations have been converted to a set of differential equations. To obtain the solution of the modeled problem, the homotopic approach has been used. The influence of imbedded physical variables upon the velocities and temperature profiles are defined and deliberated through graphs. Moreover, for the several values of relevant variables, the skin fraction coefficient and local Nusselt number are tabulated. Plots have been presented in order to examine how the velocities and temperature profile get affected by various flow parameters.
Read Full Article HTML DOI: 10.29328/journal.ijpra.1001002 Cite this Article Read Full Article PDF
Keywords:
SWCNTs; MWCNTs; Nanoparticles; Casson fluids; Thermal radiation; MHD; Parallel Plates; Rotating System; HAM
References
- Haq RU, Nadeem S, Khan ZH, Noor NFM. Convective heat transfer in MHD slips flow over a stretching surface in the presence of carbon nanotubes. Phys B Condens Matter. 2015; 457: 40-47. Ref.: https://tinyurl.com/ybhuvpbe
- Liu MS, Lin MCC, Te HI, Wang CC. Enhancement of thermal conductivity with carbon nanotube for nanofluids. Int Comm in Heat and Mass Transfer. 2015; 32: 1202-1210; Ref.: https://tinyurl.com/ycqbu7c9
- Nadeem S, Lee C. Boundary layer flow of nanofluid over an exponentially stretching surface. Nanoscale Res Lett. 2012; 7: 94. Ref.: https://tinyurl.com/ybp2rygp
- Ellahi R, Raza M, Vafai K. Series solutions of non-Newtonian nanofluids with Reynolds' model and Vogel's model by means of the homotopy analysis method. Math Comput Model. 2012; 55: 1876-1891. Ref.: https://tinyurl.com/y9tn4s3b
- Nadeem S, Haq RU, Khan ZH. Numerical study of MHD boundary layer flow of a Maxwell fluid past a stretching sheet in the presence of nanopar-ticles. J TaiwanInst Chem Eng. 2014; 45: 121-126. Ref.: https://tinyurl.com/y9hsb38v
- Nadeem S, Haq RU. MHD boundary layer flow of a nano fluid past a porous shrinking sheet with thermal radiation, J Aerospace Eng. 1943-5525. Ref.: https://tinyurl.com/y97mpwdv
- Nadeem S, Haq RU. Effect of thermal radiation for megnetohydrody- namic boundary layer flow of a nanofluid past a stretching sheet with convective boundary conditions. J Comput Theor Nanosci. 2013; 11: 32-40. Ref.: https://tinyurl.com/y96y4ddt
- Choi SUS. Enhancing thermal conductivity of fluids with nanoparticles. Int mech eng congress and exposition. 1995; 66: 99-105. Ref.: https://tinyurl.com/ycq6by6d
- Buongiorno J. Convective transport in nanofluids. J Heat Transf. 2006; 128: 240-250. Ref.: https://tinyurl.com/yamfme6z
- Sheikholeslami M. Influence of magnetic field on nanofluid free convection in an open porous cavity by means of Lattice Boltzmann method. J of Molecular Liquids. 2017; 234: 364. Ref.: https://tinyurl.com/y9yxzq6f
- Sheikholeslami M. Magnetic field influence on nanofluid thermal radiation in a cavity with tilted elliptic inner cylinder. J of Molecular Liquids. 2017; 229: 137-147. Ref.: https://tinyurl.com/y7jrhyy3
- Sheikholeslami M. Magnetohydrodynamic nanofluid forced convection in a porous lid driven cubic cavity using Lattice Boltzmann method. J of Molecular Liquids. 2017; 231: 555-565. Ref.: https://tinyurl.com/y86kyh8f
- Sheikholeslami M. Numerical simulation of magnetic nanofluid natural convection in porous media. Physics Letters A. 2017; 381: 494-503. Ref.: https://tinyurl.com/ybllfpc2
- Sheikholeslami M. Numerical study of heat transfer enhancement in a pipe filled with porous media by axisymmetric TLB model based on GPU. Eur Phys J Plus. 2014; 129: 248.
- Sheikholeslami M. CVFEM for magnetic nanofluid convective heat transfer in a porous curved enclosure. Eur Phys J Plus. 2016; 131: 413. Ref.: https://tinyurl.com/y99bt4sh
- Sheikholeslami M, Rokni HB. Simulation of nanofluid heat transfer in presence of magnetic field: A review. Int J of Heat and Mass Transfer. 2017; 115: 1203-1233. Ref.: https://tinyurl.com/ybahhr9g
- Sheikholeslami M, Rokni HB. Free convection of CuOeH2O nanofluid in a curved porous enclosure using mesoscopic approach. Int J of Heat and Mass Transfer. 2017; 42: 15393. Ref.: https://tinyurl.com/y8jetqnk
- Sheikholeslami M. Houman BR. Numerical simulation for impact of Coulomb force on nanofluid heat transfer in a porous enclosure in presence of thermal radiation. International Journal of Heat and Mass Transfer. 2018; 118: 823-831. Ref.: https://tinyurl.com/y99vplln
- Sheikholeslami M, Ganji DD, Javed MY, Ellahi R. Effect of thermal radiation on magnetohydrodynamics nanofluid flow and heat transfer by means of two phase model. Journal of Magnetism and Magnetic Materials. 2015; 374: 36-43. Ref.: https://tinyurl.com/y8kd9kv6
- Elias MM, Miqdad M, Mahbubul IM, Saidur R, Kamalisarvestani M, et al. Effect of nanoparticle shape on the heat transfer and thermodynamic performance of a shell and tube heat exchanger. Int Commun Heat Mass Transfer. 2013; 44: 93-99. Ref.: https://tinyurl.com/y9owqk5n
- Alfven H. Existence of electromagnetic-hydrodynamic waves. Nature. 1942; 150: 405-406. Ref.: https://tinyurl.com/y9x9jb2p
- Shah Z, Gul T, Khan AM, Ali I, Islam S. Effects of hall current on steady three dimensional non-newtonian nanofluid in a rotating frame with brownian motion and thermophoresis effects. J Eng Technol. 2017; 6: 280-296. Ref.: https://tinyurl.com/yb28z25t
- Shah Z, Islam S, Gul T, Bonyah E, Khan MA. The electrical MHD and hall current impact on micropolar nanofluid flow between rotating parallel plates. Results Phys. 2018: 9: 1201-1214. Ref.: https://tinyurl.com/ybelycjt
- Shah Z, Islam S, Gul T, Bonyah E, Khan MA. Three dimensional third grade nanofluid flow in a rotating system between parallel plates with Brownian motion and thermophoresis effects. Results Phys. 2018; 10: 36-45. Ref.: https://tinyurl.com/yc24emj2
- Casson NA. A flow equation for pigment oil suspension of printing ink type. In: Mill CC (ed) Rheology of dispersed system. Pergamon Press. Oxford. 1959.
- Mehmood Z, Mehmood R, Iqbal Z. Numerical Investigation of Micropolar Casson Fluid over a Stretching Sheet with Internal Heating. Commun Theor Phys. 2017; 67: 443-448. Ref.: https://tinyurl.com/y7xbr4rv
- Iqbal Z, Mehmood R, Ehtsham Azhar, Mehmood Z. Impact of inclined magnetic field on micropolar Casson fluid using Keller box algorithm. Eur Phys J Plus. 2017; 132: 175. Ref.: https://tinyurl.com/yarhf5cl
- Megahe AM. Effect of slip velocity on Casson thin film flow and heat transfer due to unsteady stretching sheet in presence of variable heat flux and viscous dissipation. Open Journal of Fluid Dynamic. 2016; 6: 303-320. Ref.: https://tinyurl.com/y85wxkph
- Abolbashari MH, Freidoonimehr N, Rashidi MM. Analytical modeling of entropy generation for Casson nano-fluid flow induced by a stretching surface. Advanced Powder Technology. 2016; 2: 542-552. Ref.: https://tinyurl.com/y7fxzbae
- Attia HA, Ahmed MES. Transient MHD couette flow of a Casson fluid between parallel plates with heat transfer. Ital J Pure Appl Math. 2010; 27: 19-38. Ref.: https://tinyurl.com/y8zbgv6h
- Mukhopadhyay S. Casson fluid flow and heat transfer over a nonlinearly stretching surface. Chin Phys B. 2013; 27: 074701-074705. Ref.: https://tinyurl.com/yc6purfo
- Qasim M, Noreen S. Heat transfer in the boundary layer flow of a Casson fluid over a permeable shrinking sheet with viscous dissipation. Eur Phys J Plus. 2014; 7: 129-137. Ref.: https://tinyurl.com/y9gm47zv
- Maxwell. Electricity and magnetism. 3rd ed. Clarendon, Oxford. 1904.
- Casson NA. Flow Equation for Pigment Oil Suspensions of the Printing Ink Type, Rheology of Disperse Systems. Pergamon Press: New York. NY, USA. 1959; 84-104. Ref.: https://tinyurl.com/ycb3o3z4
- Hussanan A, Salleh MZ, Tahar RM, Khan I. Unsteady boundary layer flow and heat transfer of a Casson fluid past an oscillating vertical plate with Newtonian heating. PLoS ONE. 2014; 9: e108763. Ref.: https://tinyurl.com/yaep7gfk
- Walicka A, Falicki J. Reynolds number effects in the flow of an electro rheological fluid of Casson type between fixed surface of revolution. Appl Math Comput. 2015; 250: 639-649. Ref.: https://tinyurl.com/y8yqa48z
- Hussain ST, Rizwan-ul-Haq, Khan ZH, Nadeem S. Water driven flow of carbon nanotubes in a rotating channel. Journal of Molecular Liquids. 2016; 214: 136-144. Ref.: https://tinyurl.com/ydbw4xpm
- Sheikholeslami M, Hatami D, Ganji DD. Nanofluid flow and heat transfer in a rotating system in the presence of a magnetic field. Journal of Molecular Liquids. 2014; 190: 112-120. Ref.: https://tinyurl.com/y8r7d73a
- Ishaq M, Ali G, Shah, Z, Islam S, Muhammad S. Entropy Generation on Nanofluid Thin Film Flow of Eyring–Powell Fluid with Thermal Radiation and MHD Effect on an Unsteady Porous Stretching Sheet. Entropy. 2018; 20: 412. Ref.: https://tinyurl.com/yb39tfy7
- Nasir S, Islam S, Gul T, Shah Z, Khan MA, et al. Three‑dimensional rotating flow of MHD single wall carbon nanotubes over a stretching sheet in presence of thermal radiation. Applied Nano science. 2018; 8: 1361-1378. Ref.: https://tinyurl.com/y9bpe8v9
- Hammed H, Haneef M, Shah Z, Islam S, Khan W, et al. The Combined Magneto hydrodynamic and electric field effect on an unsteady Maxwell nanofluid Flow over a Stretching Surface under the Influence of Variable Heat and Thermal Radiation. Appl Sci. 2018; 8: 160. Ref.: https://tinyurl.com/ycfnfqpn
- Ali A, M Sulaiman, S Islam, Z Shah, E Bonyah. Three-dimensional magnetohydrodynamic (MHD) flow of Maxwell nanofluid containing gyrotactic micro-organisms with heat source/sink. AIP Advances. 2018; 8: 085303. Ref.: https://tinyurl.com/yatjo8op
Figures:
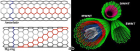
Figure 1
Figure 2

Figure 3

Figure 4

Figure 5

Figure 6

Figure 7

Figure 8

Figure 9

Figure 10

Figure 11

Figure 12

Figure 13

Figure 14

Figure 15

Figure 16

Figure 17
Similar Articles
-
Magnetohydrodynamic CNTs Casson Nanofluid and Radiative heat transfer in a Rotating ChannelsZahir Shah*,Abdullah Dawar,Saeed Islam,Muhammad Idress,Waris Khan. Magnetohydrodynamic CNTs Casson Nanofluid and Radiative heat transfer in a Rotating Channels. . 2018 doi: 10.29328/journal.ijpra.1001002; 1: 017-032
-
Biodegradation of gold and platinum implants in rats studied by electron microscopyLudwig Jonas*,Hendrik Kosslick,Hermann Sauer,Tino Just,Ursula Vick,Gerhard Fulda. Biodegradation of gold and platinum implants in rats studied by electron microscopy. . 2019 doi: 10.29328/journal.ijpra.1001014; 2: 041-048
-
Influence of high frequency rotating magnetic field on the effect of heating magnetic fluidAndrzej Skumiel*. Influence of high frequency rotating magnetic field on the effect of heating magnetic fluid. . 2021 doi: 10.29328/journal.ijpra.1001035; 4: 015-018
-
Quantum analysis of sub harmonic generation with two-mode coherent lightAlemayehu Getahun*,Habtamu Dagnew. Quantum analysis of sub harmonic generation with two-mode coherent light. . 2021 doi: 10.29328/journal.ijpra.1001037; 4: 026-030
-
Magnetohydrodynamic (MHD) stability of wendelstein7-X reactor with resistive wall (RWMs)Ali Pazirandeh*,Mehrnaz Sadat Shariati. Magnetohydrodynamic (MHD) stability of wendelstein7-X reactor with resistive wall (RWMs). . 2021 doi: 10.29328/journal.ijpra.1001039; 4: 033-038
-
Determination of the Effect of Zinc Acetate as a Doped Substance on the Properties of Cadmium Sulfide Nanomaterials by using a Hydrothermal Interaction TechniqueMohammed Rasool Ahmed, Abdulkareem Thjeel Jabbar, Abdullah Hasan Jabbar*. Determination of the Effect of Zinc Acetate as a Doped Substance on the Properties of Cadmium Sulfide Nanomaterials by using a Hydrothermal Interaction Technique. . 2023 doi: 10.29328/journal.ijpra.1001066; 6: 160-164
-
Study the Influence of Laser Energy on the Surface Morphology of Copper Nanoparticles Prepared by Pulsed Laser Extirpation Method in LiquidMohammed Rasool Ahmed*, Taghreed N Jamil and Narimann Neamah Hussein. Study the Influence of Laser Energy on the Surface Morphology of Copper Nanoparticles Prepared by Pulsed Laser Extirpation Method in Liquid. . 2023 doi: 10.29328/journal.ijpra.1001072; 6: 194-98
Recently Viewed
-
Markov Chains of Molecular Processes of Biochemical MaterialsOrchidea Maria Lecian*. Markov Chains of Molecular Processes of Biochemical Materials. Int J Phys Res Appl. 2024: doi: 10.29328/journal.ijpra.1001076; 7: 001-005
-
Generation of Curved Spacetime in Quantum FieldSarfraj Khan*. Generation of Curved Spacetime in Quantum Field. Int J Phys Res Appl. 2024: doi: 10.29328/journal.ijpra.1001077; 7: 006-009
-
Optimizing Milk Safety: Applying Nuclear Techniques in X-ray Fluorescence Spectroscopy for Heavy Metal Quantification in Powdered Milk Consumed in SenegalPapa Macoumba Faye*, Djicknack Dione, Oumar Ndiaye, Moussa Hamady SY, Nogaye Ndiaye, Alassane Traore, Ababacar Sadikhe Ndao. Optimizing Milk Safety: Applying Nuclear Techniques in X-ray Fluorescence Spectroscopy for Heavy Metal Quantification in Powdered Milk Consumed in Senegal. Int J Phys Res Appl. 2024: doi: 10.29328/journal.ijpra.1001078; 7: 010-015
-
Thermoelectric Materials Based on Lead Telluride and Prospects for their Practical ApplicationYuriy Pavlovskyy*, Nadiya Pavlovska. Thermoelectric Materials Based on Lead Telluride and Prospects for their Practical Application. Int J Phys Res Appl. 2024: doi: 10.29328/journal.ijpra.1001079; 7: 016-018
-
Approximation of Kantorovich-type Generalization of (p,q) - Bernstein type Rational Functions Via Statistical ConvergenceHayatem Hamal*. Approximation of Kantorovich-type Generalization of (p,q) - Bernstein type Rational Functions Via Statistical Convergence. Int J Phys Res Appl. 2024: doi: 10.29328/journal.ijpra.1001080; 7: 019-025
Most Viewed
-
Evaluation of Biostimulants Based on Recovered Protein Hydrolysates from Animal By-products as Plant Growth EnhancersH Pérez-Aguilar*, M Lacruz-Asaro, F Arán-Ais. Evaluation of Biostimulants Based on Recovered Protein Hydrolysates from Animal By-products as Plant Growth Enhancers. J Plant Sci Phytopathol. 2023 doi: 10.29328/journal.jpsp.1001104; 7: 042-047
-
Sinonasal Myxoma Extending into the Orbit in a 4-Year Old: A Case PresentationJulian A Purrinos*, Ramzi Younis. Sinonasal Myxoma Extending into the Orbit in a 4-Year Old: A Case Presentation. Arch Case Rep. 2024 doi: 10.29328/journal.acr.1001099; 8: 075-077
-
Feasibility study of magnetic sensing for detecting single-neuron action potentialsDenis Tonini,Kai Wu,Renata Saha,Jian-Ping Wang*. Feasibility study of magnetic sensing for detecting single-neuron action potentials. Ann Biomed Sci Eng. 2022 doi: 10.29328/journal.abse.1001018; 6: 019-029
-
Pediatric Dysgerminoma: Unveiling a Rare Ovarian TumorFaten Limaiem*, Khalil Saffar, Ahmed Halouani. Pediatric Dysgerminoma: Unveiling a Rare Ovarian Tumor. Arch Case Rep. 2024 doi: 10.29328/journal.acr.1001087; 8: 010-013
-
Physical activity can change the physiological and psychological circumstances during COVID-19 pandemic: A narrative reviewKhashayar Maroufi*. Physical activity can change the physiological and psychological circumstances during COVID-19 pandemic: A narrative review. J Sports Med Ther. 2021 doi: 10.29328/journal.jsmt.1001051; 6: 001-007

HSPI: We're glad you're here. Please click "create a new Query" if you are a new visitor to our website and need further information from us.
If you are already a member of our network and need to keep track of any developments regarding a question you have already submitted, click "take me to my Query."