Abstract
Review Article
Finite-time thermodynamics: Realizability domains of thermodynamic systems and P. Salamon’s problem of efficiency corresponding to maximum power output of the system
Tsirlin AM* and Sukin IA
Published: 16 October, 2018 | Volume 1 - Issue 1 | Pages: 052-066
The paper analyses performance boundaries of systems converting the heat energy into the mechanical or separation work. Authors approach this problem from the view-point of the finite-time thermodynamics. Using thermodynamic balance equations, authors provide the algorithm for calculation of realizability domain for such systems. The paper shows that the performance of these systems is the upper bounded function of the heat flux, assuming that heat and mass transfer coefficients are given. Authors present sufficient conditions under which the efficiency (specific heat flux per unit of the useful flux) of the system does not depend on kinetic coefficients when operating in the maximum performance mode. The paper shows how to use these conditions to optimally choose the separation order for multicomponent distillation.
Read Full Article HTML DOI: 10.29328/journal.ijpra.1001004 Cite this Article Read Full Article PDF
References
- Bosnjakovic F. Technical Thermodynamics. Holt, Rinehart & Winston of Canada Ltd. 1965. Ref.: https://goo.gl/jTaCGG
- Green D, Perry R. Perry’s Chemical Engineers’ Handbook. Eighth Edition. McGraw-Hill Education. 2007. Ref.: https://goo.gl/nWFaf8
- Tsirlin A. Neobratimye otsenki predelnykh vozmozhnostej termodinamicheskikh i mikroekonomicheskikh sistem (in Russian). Moscow: Nauka. 2003.
- Novikov I. The efficiency of atomic power stations. J Nucl Energy II. 1954; 7: 125-128. Ref.: https://goo.gl/51XW3r
- Dincer I, Rosen M. Exergy. 2nd Edition. Elsevier Science. 2012. Ref.: https://goo.gl/smUXYj
- Salamon P, Nulton J, Andresen B, Roach T, Felts B, et al. Application of finite-time and control thermodynamics to biological processes at multiple scales. J Non-Equilib Thermodyn. 2018; 43: 193-210. Ref.: https://goo.gl/utMwzW
- Schwalbe K, Hoffman K. Optimal control of an endoreversible solar power plant. J Non-Equilib Thermodyn. 2018; 43: 255-271. Ref.: https://goo.gl/U1BYbG
- Chen L, Yan Z. The effect of heat transfer law on the performance of a two-heat-source endoreversible cycle. J Chem Phys. 1989; 90: 3740-3743. Ref.: https://goo.gl/aobmXC
- Chen L, Sun F, Wu C. Effect of heat transfer law on the performance of a generalized irreversible carnot engine. J Phys D: Appl Phys. 1999; 32: 99-105. Ref.: https://goo.gl/TPhjzT
- Chen L, Li J, Sun F. Generalized irreversible heat engine experiencing a complex heat transfer law. Appl Energy. 2008; 85: 52-60. Ref.: https://goo.gl/3M56Se
- de Vos A. Efficiency of some heat engines at maximum power conditions. Am J Phys. 1984; 53: 570-573. Ref.: https://goo.gl/k4FvND
- Song H, Chen L, Li J, Sun F. Optimal configuration of a class of endoreversible heat engines with linear phenomenological heat transfer law. J Appl Phys. 2006; 100. Ref.: https://goo.gl/E8R7RB
- Song H, Chen L, Sun F. Endoreversible heat engines for maximum power output with fixed duration and radiative heat-transfer law. Appl Energy. 2007; 84: 374-388. Ref.: https://goo.gl/8astj3
- Song H, Chen L, Sun F, Wang S. Configuration of heat engines for maximum power output with fixed compression ratio and generalized radiative heat transfer law. J Non-Equilib Thermodyn. 2008; 33: 275-295. Ref.: https://goo.gl/WauJ83
- Li J, Chen L, Sun F. Optimal configuration of a class of endoreversible heat-engines for maximum power-output with linear phenomenological heat-transfer law. Appl Energy. 2007; 84: 944-957. Ref.: https://goo.gl/Q6KPoY
- Chen L, Song H, Sun F, Wang S. Optimal configuration of heat engines for maximum efficiency with generalized radiative heat transfer law. Rev Mex Fis. 2009; 55: 55-67. Ref.: https://goo.gl/wFkffM
- Ares De Parga G, Angulo-Brown F, Navarrete-Gonzalez T. A variational optimization of a finite-time thermal cycle with a nonlinear heat transfer law. Energy. 1999; 24: 997-1008. Ref.: https://goo.gl/LSv2Q4
- Ait-Ali M. The maximum coefficient of performance of internally irreversible refrigerators and heat pumps. J Phys D: Appl Phys. 1996; 29: 975-980. Ref.: https://goo.gl/AX4LNJ
- Rozonoer L, Tsirlin A. Optimal control of thermodynamic processes i–iii. Autom Remote Control. 1983; 44: 314-326. Ref.: https://goo.gl/4p6Hex
- Tsirlin A, Sukin I. Finite-time thermodynamics: The maximal productivity of binary distillation and selection of optimal separation sequence for an ideal ternary mixture. J Non-Equilib Thermodyn. 2014; 39: 13-25. Ref.: https://goo.gl/mg5uJE
- Tsirlin A, Sukin I. Attainability region of binary distillation and separation sequence of three-component mixture. Theor Found Chem Eng. 2014; 48: 764-775. Ref.: https://goo.gl/bERV7e
Figures:
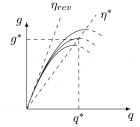
Figure 1
Similar Articles
-
High energy HF (DF) lasersVictor V Apollonov*. High energy HF (DF) lasers. . 2018 doi: 10.29328/journal.ijpra.1001001; 1: 001-016
-
Magnetohydrodynamic CNTs Casson Nanofluid and Radiative heat transfer in a Rotating ChannelsZahir Shah*,Abdullah Dawar,Saeed Islam,Muhammad Idress,Waris Khan. Magnetohydrodynamic CNTs Casson Nanofluid and Radiative heat transfer in a Rotating Channels. . 2018 doi: 10.29328/journal.ijpra.1001002; 1: 017-032
-
Sounding procedure for characterization of big fusion reactor chambers by means of a compact neutron source with a nanosecond pulse durationVA Gribkov*,B Bienkowska,S Jednorog,M Paduch,Tomaszewski. Sounding procedure for characterization of big fusion reactor chambers by means of a compact neutron source with a nanosecond pulse duration. . 2018 doi: 10.29328/journal.ijpra.1001003; 1: 033-051
-
Gravitation - Flat Power FieldSA Orlov*. Gravitation - Flat Power Field. . 2018 doi: 10.29328/journal.ijpra.1001005; 1: 067-073
-
Moving space-matter as the basis of the intelligence in the Physical WorldBoris S Dizhechko*. Moving space-matter as the basis of the intelligence in the Physical World. . 2019 doi: 10.29328/journal.ijpra.1001007; 2: 001-003
-
Nanotechnology to improve the biofouling and corrosion performance of marine paints: from lab experiments to real tests in seaGeorge Kordas*. Nanotechnology to improve the biofouling and corrosion performance of marine paints: from lab experiments to real tests in sea. . 2019 doi: 10.29328/journal.ijpra.1001012; 2: 033-037
-
Biological membranes: The laboratory of fundamental physicsSamo Kralj*,Mitja Kralj. Biological membranes: The laboratory of fundamental physics. . 2019 doi: 10.29328/journal.ijpra.1001013; 2: 038-040
-
Biodegradation of gold and platinum implants in rats studied by electron microscopyLudwig Jonas*,Hendrik Kosslick,Hermann Sauer,Tino Just,Ursula Vick,Gerhard Fulda. Biodegradation of gold and platinum implants in rats studied by electron microscopy. . 2019 doi: 10.29328/journal.ijpra.1001014; 2: 041-048
-
Modeling of A.I based Inhalation for Advanced Life Support System DevelopmentMd. Sadique Shaikh*,Tanvir Begum. Modeling of A.I based Inhalation for Advanced Life Support System Development. . 2019 doi: 10.29328/journal.ijpra.1001015; 2: 049-050
-
Bio-moleculear thermal oscillator and constant heat current sourceR Panahinia*,S Behnia. Bio-moleculear thermal oscillator and constant heat current source. . 2019 doi: 10.29328/journal.ijpra.1001016; 2: 051-055
Recently Viewed
-
Endoscopic treatment of pancreatic diseases via Duodenal Minor Papilla: 135 cases treated by Sphincterotomy, Endoscopic Pancreatic Duct Balloon Dilation (EPDBD), and Pancreatic Stenting (EPS)Tadao Tsuji*, G Sun,A Sugiyama, Y Amano,S Mano,T Shinobi,H Tanaka,M Kubochi,K Ohishi,Y Moriya,M Ono,T Masuda, H Shinozaki,H Kaneda,H Katsura,T Mizutani, K Miura,M Katoh, K Yamafuji, K Takeshima,N Okamoto,Y Hoshino,N Tsurumi,S Hisada,J Won,T Kogiso,K Yatsuji,M Iimura, T Kakimoto,S Nyuhzuki. Endoscopic treatment of pancreatic diseases via Duodenal Minor Papilla: 135 cases treated by Sphincterotomy, Endoscopic Pancreatic Duct Balloon Dilation (EPDBD), and Pancreatic Stenting (EPS) . Ann Clin Gastroenterol Hepatol. 2019: doi: 10.29328/journal.acgh.1001009; 3: 012-019
-
Euthanasia: Growing Acceptance amid Lingering ReluctanceTshibambe N Tshimbombu,Immanuel Olarinde,Judea Wiggins*,Maxwell Vergo. Euthanasia: Growing Acceptance amid Lingering Reluctance. Clin J Nurs Care Pract. 2025: doi: 10.29328/journal.cjncp.1001058; 9: 001-006
-
Various Theories of Fast and Ultrafast Magnetization DynamicsManfred Fähnle*. Various Theories of Fast and Ultrafast Magnetization Dynamics. Int J Phys Res Appl. 2024: doi: 10.29328/journal.ijpra.1001101; 7: 154-158
-
Nitrogen Fixation and Yield of Common Bean Varieties in Response to Shade and Inoculation of Common BeanSelamawit Assegid*,Girma Abera. Nitrogen Fixation and Yield of Common Bean Varieties in Response to Shade and Inoculation of Common Bean. J Plant Sci Phytopathol. 2023: doi: 10.29328/journal.jpsp.1001122; 7: 157-162
-
Peripheral perfusion index in critically ill COVID-19 and its association with multiorgan dysfunctionCornu Matias German*, Tonelier Matias, Roel Pedro, Sanhueza Laura, Orozco Sergio Martin, Sepulveda Mariana Elizabet, Svampa Silvana Enrica, Arana Osorio Erick and Martinuzzi Andres Luciano Nicolas. Peripheral perfusion index in critically ill COVID-19 and its association with multiorgan dysfunction. J Clin Intensive Care Med. 2023: doi: 10.29328/journal.jcicm.1001043; 8: 004-013
Most Viewed
-
Evaluation of Biostimulants Based on Recovered Protein Hydrolysates from Animal By-products as Plant Growth EnhancersH Pérez-Aguilar*, M Lacruz-Asaro, F Arán-Ais. Evaluation of Biostimulants Based on Recovered Protein Hydrolysates from Animal By-products as Plant Growth Enhancers. J Plant Sci Phytopathol. 2023 doi: 10.29328/journal.jpsp.1001104; 7: 042-047
-
Sinonasal Myxoma Extending into the Orbit in a 4-Year Old: A Case PresentationJulian A Purrinos*, Ramzi Younis. Sinonasal Myxoma Extending into the Orbit in a 4-Year Old: A Case Presentation. Arch Case Rep. 2024 doi: 10.29328/journal.acr.1001099; 8: 075-077
-
Feasibility study of magnetic sensing for detecting single-neuron action potentialsDenis Tonini,Kai Wu,Renata Saha,Jian-Ping Wang*. Feasibility study of magnetic sensing for detecting single-neuron action potentials. Ann Biomed Sci Eng. 2022 doi: 10.29328/journal.abse.1001018; 6: 019-029
-
Pediatric Dysgerminoma: Unveiling a Rare Ovarian TumorFaten Limaiem*, Khalil Saffar, Ahmed Halouani. Pediatric Dysgerminoma: Unveiling a Rare Ovarian Tumor. Arch Case Rep. 2024 doi: 10.29328/journal.acr.1001087; 8: 010-013
-
Physical activity can change the physiological and psychological circumstances during COVID-19 pandemic: A narrative reviewKhashayar Maroufi*. Physical activity can change the physiological and psychological circumstances during COVID-19 pandemic: A narrative review. J Sports Med Ther. 2021 doi: 10.29328/journal.jsmt.1001051; 6: 001-007

HSPI: We're glad you're here. Please click "create a new Query" if you are a new visitor to our website and need further information from us.
If you are already a member of our network and need to keep track of any developments regarding a question you have already submitted, click "take me to my Query."