Abstract
Opinion
Biological membranes: The laboratory of fundamental physics
Samo Kralj* and Mitja Kralj
Published: 01 November, 2019 | Volume 2 - Issue 1 | Pages: 038-040
Biological membranes present an essential constituent of living cells. Their main role is to separate the interior of a cell from its surrounding, however allowing the selective transfer of specific material through it. Configuration changes of membranes are often correlated with important biological processes [1-7].
Read Full Article HTML DOI: 10.29328/journal.ijpra.1001013 Cite this Article Read Full Article PDF
References
- Deuticke B. Transformation and restoration of biconcave shape of human erythrocytes induced by amphiphilic agents and changes of ionic environment. Biochim. Biophys. Acta. 1968; 163: 494-500. PubMed: https://www.ncbi.nlm.nih.gov/pubmed/4387277
- Iglič A, Babnik B, Gimsa U, Kralj-Iglič V. On the role of membrane anisotropy in the beading transition of undulated tubular membrane structures. J Phys A Math Gen. 2006; 38: 8527.
- Hurley JH, Boura E, Carlson LA, Różycki B. Membrane Budding. Cell. 2010; 143: 875-887. PubMed: https://www.ncbi.nlm.nih.gov/pubmed/21145455
- Jesenek D, Perutková S, Kralj-Iglič V, Kralj S, Iglič A. Exocytotic fusion pore stability and topological defects in the membrane with orientational degree of ordering. Cell Calcium. 2012; 52: 277-282. PubMed: https://www.ncbi.nlm.nih.gov/pubmed/22541648
- Lee J, Abdeen AA, Wycislo KL, Fan TM, Kilian KA. Interfacial geometry dictates cancer cell tumorigenicity. Nat Mater. 2016; 15: 856-862. PubMed: https://www.ncbi.nlm.nih.gov/pubmed/27043781
- Saw TB, Doostmohammadi A, Nier V, Kocgozlu L, Thampi S, et al. Topological defects in epithelia govern cell death and extrusion. Nature. 2017; 544: 212-216. PubMed: https://www.ncbi.nlm.nih.gov/pubmed/28406198
- Kumar G, Ramakrishnan N2, Sain A. Tubulation pattern of membrane vesicles coated with biofilaments. Phys Rev E. 2019; 99: 022414. PubMed: https://www.ncbi.nlm.nih.gov/pubmed/30934309
- Helfrich W. Elastic properties of lipid bilayers: theory and possible experiments. Zeits Naturforschung. 1973; 28: 693-703. PubMed: https://www.ncbi.nlm.nih.gov/pubmed/4273690
- Kralj-Iglič V, Heinrich V, Svetina S, Žekš B. Free energy of closed membrane with anisotropic inclusions. Eur Phys J B. 1999; 10: 5-8.
- Perutková Š, Daniel M, Rappolt M, Pabst G, Dolinar G, et al., Elastic deformations in hexagonal phases studied by small-angle X-ray diffraction and simulations. Phys Chem Chem Phys. 2011; 13: 3100-3107. PubMed: https://www.ncbi.nlm.nih.gov/pubmed/21063616
- Fournier JB. Nontopological saddle-splay and curvature instabilities from anisotropic membrane inclusions. Phys Rev Lett. 1996; 76: 4436-4439. PubMed: https://www.ncbi.nlm.nih.gov/pubmed/10061289
- Mermin ND. The topological theory of defects in ordered media. Rev Mod Phys. 1979; 51: 591.
- Mesarec L, Góźdź W, Iglič A, Kralj S. Effective topological charge cancelation mechanism. Sci Rep. 2016; 6: 27117.
- Kamien RD. The topological theory of defects in ordered media. Rev Mod Phys. 2002; 74: 953.
- Bowick M, Nelson DR, Travesset A. Curvature-induced defect unbinding in toroidal geometries. Phys Rev E. 2004; 69: 041102.
- Kralj-Iglic V, Iglic A, Hägerstrand H, Peterlin P. Stable tubular microexovesicles of the erythrocyte membrane induced by dimeric amphiphiles. Phys Rev E. 2000; 61: 4230. PubMed: https://www.ncbi.nlm.nih.gov/pubmed/11088219
- Selinger RL, Konya A, Travesset A, Selinger JV. Monte Carlo studies of the XY model on two-dimensional curved surfaces. J Phys Chem B. 2011; 115: 13989-13993. PubMed: https://www.ncbi.nlm.nih.gov/pubmed/21970652
- Napoli G, Vergori L. extrinsic curvature effects on nematic shells. Phys Rev Lett. 2012; 108: 207803. PubMed: https://www.ncbi.nlm.nih.gov/pubmed/23003189
- Kibble TWB. Topology of cosmic domains and strings. J Phys A Math Gen. 1976; 9: 1387.
- Zurek WH. Cosmological experiments in superfluid helium? Nature. 1985; 317: 505.
- Giblin JT, Mertens JB, Starkman GD. Departures from the Friedmann-Lemaitre-Robertson-Walker Cosmological Model in an Inhomogeneous Universe: A numerical Examination. Phys Rev Lett. 2016; 116: 251301. PubMed: https://www.ncbi.nlm.nih.gov/pubmed/27391710
- Hobson A. There are no particles, there are only fields. Am J Phys. 2013; 81: 211-223.
- Skyrme T. A unified field theory of mesons and baryons. Nucl Phys. 1962; 31: 556-559.
Figures:

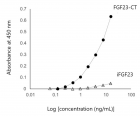
Figure 1

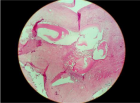
Figure 2
Similar Articles
-
High energy HF (DF) lasersVictor V Apollonov*. High energy HF (DF) lasers. . 2018 doi: 10.29328/journal.ijpra.1001001; 1: 001-016
-
Magnetohydrodynamic CNTs Casson Nanofluid and Radiative heat transfer in a Rotating ChannelsZahir Shah*,Abdullah Dawar,Saeed Islam,Muhammad Idress,Waris Khan. Magnetohydrodynamic CNTs Casson Nanofluid and Radiative heat transfer in a Rotating Channels. . 2018 doi: 10.29328/journal.ijpra.1001002; 1: 017-032
-
Sounding procedure for characterization of big fusion reactor chambers by means of a compact neutron source with a nanosecond pulse durationVA Gribkov*,B Bienkowska,S Jednorog,M Paduch,Tomaszewski. Sounding procedure for characterization of big fusion reactor chambers by means of a compact neutron source with a nanosecond pulse duration. . 2018 doi: 10.29328/journal.ijpra.1001003; 1: 033-051
-
Gravitation - Flat Power FieldSA Orlov*. Gravitation - Flat Power Field. . 2018 doi: 10.29328/journal.ijpra.1001005; 1: 067-073
-
Moving space-matter as the basis of the intelligence in the Physical WorldBoris S Dizhechko*. Moving space-matter as the basis of the intelligence in the Physical World. . 2019 doi: 10.29328/journal.ijpra.1001007; 2: 001-003
-
Nanotechnology to improve the biofouling and corrosion performance of marine paints: from lab experiments to real tests in seaGeorge Kordas*. Nanotechnology to improve the biofouling and corrosion performance of marine paints: from lab experiments to real tests in sea. . 2019 doi: 10.29328/journal.ijpra.1001012; 2: 033-037
-
Biological membranes: The laboratory of fundamental physicsSamo Kralj*,Mitja Kralj. Biological membranes: The laboratory of fundamental physics. . 2019 doi: 10.29328/journal.ijpra.1001013; 2: 038-040
-
Biodegradation of gold and platinum implants in rats studied by electron microscopyLudwig Jonas*,Hendrik Kosslick,Hermann Sauer,Tino Just,Ursula Vick,Gerhard Fulda. Biodegradation of gold and platinum implants in rats studied by electron microscopy. . 2019 doi: 10.29328/journal.ijpra.1001014; 2: 041-048
-
Modeling of A.I based Inhalation for Advanced Life Support System DevelopmentMd. Sadique Shaikh*,Tanvir Begum. Modeling of A.I based Inhalation for Advanced Life Support System Development. . 2019 doi: 10.29328/journal.ijpra.1001015; 2: 049-050
-
Bio-moleculear thermal oscillator and constant heat current sourceR Panahinia*,S Behnia. Bio-moleculear thermal oscillator and constant heat current source. . 2019 doi: 10.29328/journal.ijpra.1001016; 2: 051-055
Recently Viewed
-
Sensitivity and Intertextile variance of amylase paper for saliva detectionAlexander Lotozynski*. Sensitivity and Intertextile variance of amylase paper for saliva detection. J Forensic Sci Res. 2020: doi: 10.29328/journal.jfsr.1001017; 4: 001-003
-
Extraction of DNA from face mask recovered from a kidnapping sceneBassey Nsor*,Inuwa HM. Extraction of DNA from face mask recovered from a kidnapping scene. J Forensic Sci Res. 2022: doi: 10.29328/journal.jfsr.1001029; 6: 001-005
-
The Ketogenic Diet: The Ke(y) - to Success? A Review of Weight Loss, Lipids, and Cardiovascular RiskAngela H Boal*, Christina Kanonidou. The Ketogenic Diet: The Ke(y) - to Success? A Review of Weight Loss, Lipids, and Cardiovascular Risk. J Cardiol Cardiovasc Med. 2024: doi: 10.29328/journal.jccm.1001178; 9: 052-057
-
Could apple cider vinegar be used for health improvement and weight loss?Alexander V Sirotkin*. Could apple cider vinegar be used for health improvement and weight loss?. New Insights Obes Gene Beyond. 2021: doi: 10.29328/journal.niogb.1001016; 5: 014-016
-
Maximizing the Potential of Ketogenic Dieting as a Potent, Safe, Easy-to-Apply and Cost-Effective Anti-Cancer TherapySimeon Ikechukwu Egba*,Daniel Chigbo. Maximizing the Potential of Ketogenic Dieting as a Potent, Safe, Easy-to-Apply and Cost-Effective Anti-Cancer Therapy. Arch Cancer Sci Ther. 2025: doi: 10.29328/journal.acst.1001047; 9: 001-005
Most Viewed
-
Evaluation of Biostimulants Based on Recovered Protein Hydrolysates from Animal By-products as Plant Growth EnhancersH Pérez-Aguilar*, M Lacruz-Asaro, F Arán-Ais. Evaluation of Biostimulants Based on Recovered Protein Hydrolysates from Animal By-products as Plant Growth Enhancers. J Plant Sci Phytopathol. 2023 doi: 10.29328/journal.jpsp.1001104; 7: 042-047
-
Sinonasal Myxoma Extending into the Orbit in a 4-Year Old: A Case PresentationJulian A Purrinos*, Ramzi Younis. Sinonasal Myxoma Extending into the Orbit in a 4-Year Old: A Case Presentation. Arch Case Rep. 2024 doi: 10.29328/journal.acr.1001099; 8: 075-077
-
Feasibility study of magnetic sensing for detecting single-neuron action potentialsDenis Tonini,Kai Wu,Renata Saha,Jian-Ping Wang*. Feasibility study of magnetic sensing for detecting single-neuron action potentials. Ann Biomed Sci Eng. 2022 doi: 10.29328/journal.abse.1001018; 6: 019-029
-
Pediatric Dysgerminoma: Unveiling a Rare Ovarian TumorFaten Limaiem*, Khalil Saffar, Ahmed Halouani. Pediatric Dysgerminoma: Unveiling a Rare Ovarian Tumor. Arch Case Rep. 2024 doi: 10.29328/journal.acr.1001087; 8: 010-013
-
Physical activity can change the physiological and psychological circumstances during COVID-19 pandemic: A narrative reviewKhashayar Maroufi*. Physical activity can change the physiological and psychological circumstances during COVID-19 pandemic: A narrative review. J Sports Med Ther. 2021 doi: 10.29328/journal.jsmt.1001051; 6: 001-007

HSPI: We're glad you're here. Please click "create a new Query" if you are a new visitor to our website and need further information from us.
If you are already a member of our network and need to keep track of any developments regarding a question you have already submitted, click "take me to my Query."