Abstract
Research Article
Unsteady and Incompressible Magneto-Hydrodynamics Blood Flow in an Inclined Cylindrical Channel
Liaqat Hussain*, Salah Uddin and Asif Shahzad
Published: 18 August, 2023 | Volume 6 - Issue 2 | Pages: 154-159
In the current study, the blood flow through an inclined cylindrical tube subjected to an external magnetic field is evaluated. The blood flow has been considered under the consequence of a transverse magnetic field. Previously the mathematical model was solved by using Caputo-Fabrizio (CF) fractional order derivative with a non-singular kernel which has the limitations like it fails to satisfy the fundamental theorem of fractional calculus. Whereas, in the present study Adomian Decomposition Method (ADM) which is suitable for all types of linear and non-linear differential equations is used. The flow of magnetized blood in an inclined cylindrical tube has been studied by using the ADM. An external magnetic field and an oscillating pressure gradient drove the blood flow. ADM algorithm has been developed and used to find the Adomian solution. Computer software MATHEMATICA has been used to visualize the influence of various flow characteristics such as Hartmann number (Ha), different radial locations and angle of inclination on the Adomian velocity. Due to the Lorentz effect and central radial location, the results show that the magnetic field diminishes the velocities of blood. Meanwhile, progressive inclination angle enhanced the blood flow.
Read Full Article HTML DOI: 10.29328/journal.ijpra.1001065 Cite this Article Read Full Article PDF
References
- Bogoliubov NN, Mitropol?skij JA, Mitropol'skii IA, Mitropolsky YA, Asymptotic methods in the theory of non-linear oscillations. 1961; 0-677-20050-1, 10, CRC Press.
- Sheikh NA, Ching DLC, Khan I. A comprehensive review on theoretical aspects of nanofluids: exact solutions and analysis. Symmetry. 2020; 12: 1-24.
- Higashi T, Yamagishi A, Takeuchi T, Kawaguchi N, Sagawa S, Onishi S, Date M. Orientation of erythrocytes in a strong static magnetic field. Blood. 1993 Aug 15;82(4):1328-34. PMID: 8353291.
- Srivastava N. Analysis of Flow Characteristics of the Blood Flowing through an Inclined Tapered Porous Artery with Mild Stenosis under the Influence of an Inclined Magnetic Field. J Biophys. 2014;2014:797142. doi: 10.1155/2014/797142. Epub 2014 Feb 25. PMID: 24719614; PMCID: PMC3955598.
- Hayat T, Qayyum S, Alsaedi A, Asghar S. Radiation effects on the mixed convection flow induced by an inclined stretching cylinder with non-uniform heat source/sink. PLoS One. 2017 Apr 25;12(4):e0175584. doi: 10.1371/journal.pone.0175584. PMID: 28441392; PMCID: PMC5404794.
- Diethelm K, Garrappa P, Giusti A, Stynes M. Why fractional derivatives with non-singular kernels should not be used. 2020; 23: 610-634.
- Atangana A, Secer A. A Note on Fractional order Derivatives and Table of Fractional Derivatives of some special functions. 2013; 8.
- Matlob MA, Jamali Y. The Concepts and Applications of Fractional Order Differential Calculus in Modeling of Viscoelastic Systems: A Primer. Crit Rev Biomed Eng. 2019;47(4):249-276. doi: 10.1615/CritRevBiomedEng.2018028368. PMID: 31679259.
- Diethelm K, Garrappa R, Giusti A, Stynes M. Why Fractional Derivatives With Nonsingular Kernels Should Not Used. 2020; 23 : 610-634.
- Dehghan M, Tatari M. The use of Adomain Decomposition Method for solving problems in calculus of variations. vol. 2006, pp. 1-12, 12-09-2005.
- Adomian G. A Review of the Decomposition Method in applied Matthematics. 1988; 135: 501-544.
- Das C, Wang G, Payne F. Some practical applications of magnetohydrodynamic pumping, Sensors and Actuators A: Physical. 2013; 2: 43-48.
- Bali, & U. Awasthi, "Mathematical model of blood flow in small blood vessel in the presence of magnetic field" Applied Mathematics, vol. 2 no. 2 pp. 264-269, 2011.
- Sharma MK, Singh K, Bansal S. Pulsatile MHD flow in an inclined catheterized stenosed artery with slip on the wall. Journal of Biomedical Science and Engineering. 2014; 7: 194-207.
- Hatami M, Hatami J, Ganji DD. Computer simulation of MHD blood conveying gold nanoparticles as a third grade non-Newtonian nanofluid in a hollow porous vessel. Comput Methods Programs Biomed. 2014 Feb;113(2):632-41. doi: 10.1016/j.cmpb.2013.11.001. Epub 2013 Nov 13. PMID: 24286727.
- Bansi CDK, Tabi CB, Motsumi TG, Mohamadou A. Fractional blood flow in oscillatory arteries with thermal radiation and magnetic field effects. Journal of Magnetism and Magnetic Materials. 2018; 456: 38-45.
- Tassaddiq A. Impact of Cattaneo-Christov heat flux model on MHD hybrid nano-micropolar fluid flow and heat transfer with viscous and joule dissipation effects. Sci Rep. 2021 Jan 11;11(1):67. doi: 10.1038/s41598-020-77419-x. PMID: 33431877; PMCID: PMC7801391.
- Vaidya H, Rajashekhar C, Prasad KV, Khan SU, Mebarek-Oudina F, Patil A, Nagathan P. Channel flow of MHD bingham fluid due to peristalsis with multiple chemical reactions: an application to blood flow through narrow arteries. SN Applied Sciences. 2021; 3: 1-12.
- Alghamdi W, Alsubie A, Kumam P, Saeed A, Gul T. MHD hybrid nanofluid flow comprising the medication through a blood artery. Sci Rep. 2021 Jun 2;11(1):11621. doi: 10.1038/s41598-021-91183-6. PMID: 34079026; PMCID: PMC8172945.
- Nisar Z, Hayat T, Alsaedi A, Ahmad B. Wall properties and convective conditions in MHD radiative peristalsis flow of Eyring-Powell nanofluid. Journal of Thermal Analysis and Calorimetry. 2021; 144: 1199-1208.
- Politis AK, Stavropoulos GP, Christolis MN, Panagopoulos FG, Vlachos NS, Markatos NC. Numerical modeling of simulated blood flow in idealized composite arterial coronary grafts: steady state simulations. J Biomech. 2007;40(5):1125-36. doi: 10.1016/j.jbiomech.2006.05.008. Epub 2006 Jul 7. PMID: 16828103.
- Koriko OK, Animasaun IL, Mahanthesh B, Saleem S, Sarojamma G, Sivaraj R. Heat transfer in the flow of blood?gold Carreau nanofluid induced by partial slip and buoyancy. Heat Transfer-Asian Research. 2018; 47: 806-823.
- Ijaz S, Iqbal Z, Maraj EN, Nadeem S. Investigation of Cu-CuO/blood mediated transportation in stenosed artery with unique features for theoretical outcomes of hemodynamics. Journal of Molecular Liquids. 2018; 254: 421-432.
- Foong LK, Shirani N, Toghraie D, Zarringhalam M, Afrand M. Numerical simulation of blood flow inside an artery under applying constant heat flux using Newtonian and non-Newtonian approaches for biomedical engineering. Comput Methods Programs Biomed. 2020 Jul;190:105375. doi: 10.1016/j.cmpb.2020.105375. Epub 2020 Jan 31. PMID: 32036202.
- Bharathi V, Vijayaragavan R, Prakash J. Comparative analysis of Cu/blood and Cu-CuO/blood nanofluids on a peristaltic flow governed by an asymmetric channel. Heat Transfer. 2020; 49: 4923-4944.
- Chen I, Sana S. Analysis of an intensive magnetic field on blood flow: part 2. Journal of Bioelectricity. 1985; 4: 55-62.
- Jang J, Lee SS. Theoretical and experimental study of MHD (magnetohydrodynamic) micropump. Sensors and Actuators A: Physical. 2000; 80: 84-89.
- Rana BMJ, Arifuzzaman SM, Islam S, Reza-E-Rabbi S, Al-Mamun A, Mazumder M, Khan MS. Swimming of microbes in blood flow of nano-bioconvective Williamson fluid. Thermal Science and Engineering Progress. 2021; 25: 101018.
- Khan U, Zaib A, Khan I, Nisar KS. Insight into the dynamics of transient blood conveying gold nanoparticles when entropy generation and Lorentz force are significant. International Communications in Heat and Mass Transfer. 2021; 127: 105415.
- Zaman NA, Sajid M. Slip effects on unsteady non-Newtonian blood flow through an inclined catheterized overlapping stenotic artery. AIP Advances. 2016; 6: 10-13.
Figures:
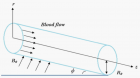
Figure 1
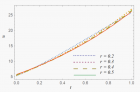
Figure 2
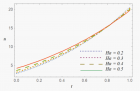
Figure 3
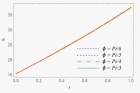
Figure 4
Similar Articles
-
High energy HF (DF) lasersVictor V Apollonov*. High energy HF (DF) lasers. . 2018 doi: 10.29328/journal.ijpra.1001001; 1: 001-016
-
Magnetohydrodynamic CNTs Casson Nanofluid and Radiative heat transfer in a Rotating ChannelsZahir Shah*,Abdullah Dawar,Saeed Islam,Muhammad Idress,Waris Khan. Magnetohydrodynamic CNTs Casson Nanofluid and Radiative heat transfer in a Rotating Channels. . 2018 doi: 10.29328/journal.ijpra.1001002; 1: 017-032
-
Sounding procedure for characterization of big fusion reactor chambers by means of a compact neutron source with a nanosecond pulse durationVA Gribkov*,B Bienkowska,S Jednorog,M Paduch,Tomaszewski. Sounding procedure for characterization of big fusion reactor chambers by means of a compact neutron source with a nanosecond pulse duration. . 2018 doi: 10.29328/journal.ijpra.1001003; 1: 033-051
-
Gravitation - Flat Power FieldSA Orlov*. Gravitation - Flat Power Field. . 2018 doi: 10.29328/journal.ijpra.1001005; 1: 067-073
-
Moving space-matter as the basis of the intelligence in the Physical WorldBoris S Dizhechko*. Moving space-matter as the basis of the intelligence in the Physical World. . 2019 doi: 10.29328/journal.ijpra.1001007; 2: 001-003
-
Nanotechnology to improve the biofouling and corrosion performance of marine paints: from lab experiments to real tests in seaGeorge Kordas*. Nanotechnology to improve the biofouling and corrosion performance of marine paints: from lab experiments to real tests in sea. . 2019 doi: 10.29328/journal.ijpra.1001012; 2: 033-037
-
Biological membranes: The laboratory of fundamental physicsSamo Kralj*,Mitja Kralj. Biological membranes: The laboratory of fundamental physics. . 2019 doi: 10.29328/journal.ijpra.1001013; 2: 038-040
-
Biodegradation of gold and platinum implants in rats studied by electron microscopyLudwig Jonas*,Hendrik Kosslick,Hermann Sauer,Tino Just,Ursula Vick,Gerhard Fulda. Biodegradation of gold and platinum implants in rats studied by electron microscopy. . 2019 doi: 10.29328/journal.ijpra.1001014; 2: 041-048
-
Modeling of A.I based Inhalation for Advanced Life Support System DevelopmentMd. Sadique Shaikh*,Tanvir Begum. Modeling of A.I based Inhalation for Advanced Life Support System Development. . 2019 doi: 10.29328/journal.ijpra.1001015; 2: 049-050
-
Bio-moleculear thermal oscillator and constant heat current sourceR Panahinia*,S Behnia. Bio-moleculear thermal oscillator and constant heat current source. . 2019 doi: 10.29328/journal.ijpra.1001016; 2: 051-055
Recently Viewed
-
Association Between Electrocardiographic Abnormalities and In-Hospital Adverse Outcome in COVID-19 PatientsAnjuman Begum*, Wadud Chowdhury, Suman KS, Arnab KC, Md. Akteruzzaman, Barua Sushanta. Association Between Electrocardiographic Abnormalities and In-Hospital Adverse Outcome in COVID-19 Patients. J Cardiol Cardiovasc Med. 2024: doi: 10.29328/journal.jccm.1001196; 9: 148-152
-
Maximizing the Potential of Ketogenic Dieting as a Potent, Safe, Easy-to-Apply and Cost-Effective Anti-Cancer TherapySimeon Ikechukwu Egba*,Daniel Chigbo. Maximizing the Potential of Ketogenic Dieting as a Potent, Safe, Easy-to-Apply and Cost-Effective Anti-Cancer Therapy. Arch Cancer Sci Ther. 2025: doi: 10.29328/journal.acst.1001047; 9: 001-005
-
Parents’ perception of the school nurse’s roleDiane Gillooly*,Ganga Mahat,Patricia Paradiso. Parents’ perception of the school nurse’s role. J Adv Pediatr Child Health. 2020: doi: 10.29328/journal.japch.1001021; 3: 064-067
-
Plant growth, Yield and Leaf Nutritional value of Jute (Corchorus olitorius L.) as Influenced by Banana Peel levels under Salt Stress conditions in Coastal region of CameroonMathias Julien Hand*,Chimène Fanta Abib,Kingsley Mbi Tabi,Alphonse Ervé Nouck,Libert Brice Tonfack,Victor Désiré Taffouo,Emmanuel Youmbi. Plant growth, Yield and Leaf Nutritional value of Jute (Corchorus olitorius L.) as Influenced by Banana Peel levels under Salt Stress conditions in Coastal region of Cameroon. J Plant Sci Phytopathol. 2024: doi: 10.29328/journal.jpsp.1001145; 8: 131-140
-
Dynamics of Siberian Fir Stands in Forest Ecosystems of Eastern Sayan SpursBazhina Elena Vasil’evna*,Pavel I Aminev. Dynamics of Siberian Fir Stands in Forest Ecosystems of Eastern Sayan Spurs. J Plant Sci Phytopathol. 2024: doi: 10.29328/journal.jpsp.1001146; 8: 141-143
Most Viewed
-
Evaluation of Biostimulants Based on Recovered Protein Hydrolysates from Animal By-products as Plant Growth EnhancersH Pérez-Aguilar*, M Lacruz-Asaro, F Arán-Ais. Evaluation of Biostimulants Based on Recovered Protein Hydrolysates from Animal By-products as Plant Growth Enhancers. J Plant Sci Phytopathol. 2023 doi: 10.29328/journal.jpsp.1001104; 7: 042-047
-
Sinonasal Myxoma Extending into the Orbit in a 4-Year Old: A Case PresentationJulian A Purrinos*, Ramzi Younis. Sinonasal Myxoma Extending into the Orbit in a 4-Year Old: A Case Presentation. Arch Case Rep. 2024 doi: 10.29328/journal.acr.1001099; 8: 075-077
-
Feasibility study of magnetic sensing for detecting single-neuron action potentialsDenis Tonini,Kai Wu,Renata Saha,Jian-Ping Wang*. Feasibility study of magnetic sensing for detecting single-neuron action potentials. Ann Biomed Sci Eng. 2022 doi: 10.29328/journal.abse.1001018; 6: 019-029
-
Pediatric Dysgerminoma: Unveiling a Rare Ovarian TumorFaten Limaiem*, Khalil Saffar, Ahmed Halouani. Pediatric Dysgerminoma: Unveiling a Rare Ovarian Tumor. Arch Case Rep. 2024 doi: 10.29328/journal.acr.1001087; 8: 010-013
-
Physical activity can change the physiological and psychological circumstances during COVID-19 pandemic: A narrative reviewKhashayar Maroufi*. Physical activity can change the physiological and psychological circumstances during COVID-19 pandemic: A narrative review. J Sports Med Ther. 2021 doi: 10.29328/journal.jsmt.1001051; 6: 001-007

HSPI: We're glad you're here. Please click "create a new Query" if you are a new visitor to our website and need further information from us.
If you are already a member of our network and need to keep track of any developments regarding a question you have already submitted, click "take me to my Query."