Abstract
Prospective Study
Precessional Motion Emerging from Relativistic Component of External Force
Janusz Wolny, Radosław Strzałka* and Ireneusz Bugański
Published: 25 October, 2024 | Volume 7 - Issue 2 | Pages: 148-153
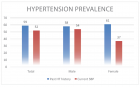
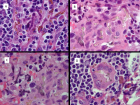
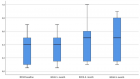
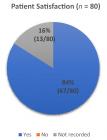
The external force in the relativistic equation of motion can be separated into two components: Fr and Fp. The first is expressed by the physical force divided by the square of the relativistic Lorentz factor, i.e γ2. This force dominates for non-relativistic velocities and vanishes for velocities approaching the speed of light c. On the other hand, the second term increases from zero with increasing velocity and dominates for velocities close to c. It is then a purely relativistic component. The characteristic feature of this component is its zero power, Fp ⋅ v = 0, but it is responsible for the relativistic precession. The effect was confirmed by numerical solutions of the equation of motion. Relativistic formulas for the precession frequency for point objects moving in selected fields of central forces were also derived analytically. It has been shown that for weak gravitational interactions, the correction for relativistic precession is small, negligibly small for Earth, and relatively small, though measurable, for Mercury. In turn, for the microworld and electrostatic forces (e.g., for the hydrogen atom), relativistic precession can fundamentally affect the movement of the electron.
Read Full Article HTML DOI: 10.29328/journal.ijpra.1001100 Cite this Article Read Full Article PDF
Keywords:
Relativity and gravitational theory; Mechanics of particles and systems
References
- Rindler W. Introduction to Special Relativity. 2nd ed. Clarendon Press; 1991. Available from: https://philpapers.org/rec/RINITS
- Wolny J, Strzałka R. Momentum in the dynamics of variable-mass systems: classical and relativistic case. Acta Phys Pol A. 2019;135:475-479. Available from: https://doi.org/10.12693/APhysPolA.135.475
- Wolny J, Strzałka R. Description of the motion of objects with sub- and superluminal speeds. Am J Phys Appl. 2020;8:25-28. Available from: http://dx.doi.org/10.11648/j.ajpa.20200802.12
- Wolny J, Strzałka R. Relativistic equation of motion in the presence of a moving force field. Novel Res Sci. 2021;6:1-5.
- Cester F, Clemente M, Korf H-M. Newton and Relativity: An alternative approach to relativistic mechanics by means of the Lex Secunda. Book on Demand; 2021.
- Einstein A. The foundation of the general theory of relativity. Ann Phys. 1916;49:769-822. Available from: http://dx.doi.org/10.1002/andp.19163540702
- Fitzpatrick R. An Introduction to Celestial Mechanics. Cambridge University Press; 2012. Available from: https://doi.org/10.1017/CBO9781139152310
- Brown K. Reflections on Relativity. Independently published.
- Kerner R, Van Holten JW, Colistete R Jr. On the quantum nature of the classical limit. Class Quant Grav. 2001;18:4725-4742. Available from: https://iopscience.iop.org/article/10.1088/0264-9381/18/22/302/meta
- Arnold VI. Mathematical Methods of Classical Mechanics. Springer Verlag; 1978. Available from: https://link.springer.com/book/10.1007/978-1-4757-1693-1
- Abramowicz MA, Kluzniak W. The origin of the deflection of light by the sun's gravitational field. Gen Rel Grav. 2003;35:69-77. Available from: https://link.springer.com/article/10.1023/A:1021354928292
- Weinberg S. Gravitation and Cosmology. New York: John Wiley and Sons; 1972.
- Dyson FW, Eddington AS, Davidson CR. A determination of the deflection of light by the sun's gravitational field, from observations made at the solar eclipse of May 29, 1919. Philos Trans R Soc A. 1920;220:291-333. Available from: https://doi.org/10.1098/rsta.1920.0009
- Phipps TE Jr. Mercury’s precession according to special relativity. Am J Phys. 1986;54:245-247. Available from: https://www.scirp.org/reference/referencespapers?referenceid=762195
- Biswas T. Minimally relativistic Newtonian gravity. Am J Phys. 1988;56:1032-1036. Available from: https://doi.org/10.1119/1.15385
- Frisch DH. Simple aspects of post-Newtonian gravitation. Am J Phys. 1990;58:332-337. Available from: https://doi.org/10.1119/1.16165
- Jefimenko OD. Gravitation and Cogravitation. Star City: Electret Scientific Company; 2006.
- de Matos CJ, Tajmar M. Advance of Mercury perihelion explained by cogravity. Available from: https://arxiv.org/ftp/gr-qc/papers/0304/0304104.pdf
- Wayne R. Explanation of the perihelion motion of Mercury in terms of a velocity-dependent correction to Newton’s law of gravitation. Afr Rev Phys. 2015;10:26. Available from: http://lamp.ictp.it/index.php/aphysrev/article/viewArticle/1074
- Lemmon TJ, Mondragon AR. Kepler’s orbits and special relativity in introductory classical mechanics. Available from: https://doi.org/10.48550/arXiv.1012.5438
- Hansen D, Hartong J, Obers NA. Action principle for Newtonian gravity. Phys Rev Lett. 2019;122:061106. Available from: https://doi.org/10.1103/PhysRevLett.122.061106
- Corda C. The secret of planets’ perihelion between Newton and Einstein. Phys Dark Universe. 2021;32:100834. Available from: https://doi.org/10.1016/j.dark.2021.100834
- Williams DR. Mercury fact sheet. 2024. Available from: http://nssdc.gsfc.nasa.gov/planetary/factsheet/mercuryfact.html
- Park RS, Folkner WM, Konopliv AS, Williams JG, Smith DE, Zuber MT. Precession of Mercury's perihelion from ranging to the MESSENGER spacecraft. Astron J. 2017;153:121-128. Available from: https://iopscience.iop.org/article/10.3847/1538-3881/aa5be2/meta
Figures:

Figure 1

Figure 2
Similar Articles
Recently Viewed
-
Pneumothorax as Complication of CT Guided Lung Biopsy: Frequency, Severity and Assessment of Risk FactorsGaurav Raj*,Neha Kumari,Neha Singh,Kaustubh Gupta,Anurag Gupta,Pradyuman Singh,Hemant Gupta. Pneumothorax as Complication of CT Guided Lung Biopsy: Frequency, Severity and Assessment of Risk Factors. J Radiol Oncol. 2025: doi: 10.29328/journal.jro.1001075; 9: 012-016
-
The Police Power of the National Health Surveillance Agency – ANVISADimas Augusto da Silva*,Rafaela Marinho da Silva. The Police Power of the National Health Surveillance Agency – ANVISA. Arch Cancer Sci Ther. 2024: doi: 10.29328/journal.acst.1001046; 8: 063-076
-
A Comparative Study of Serum Sodium and Potassium Levels across the Three Trimesters of PregnancyOtoikhila OC and Seriki SA*. A Comparative Study of Serum Sodium and Potassium Levels across the Three Trimesters of Pregnancy. Clin J Obstet Gynecol. 2023: doi: 10.29328/journal.cjog.1001137; 6: 108-116
-
Chaos to Cosmos: Quantum Whispers and the Cosmic GenesisOwais Farooq*,Romana Zahoor*. Chaos to Cosmos: Quantum Whispers and the Cosmic Genesis. Int J Phys Res Appl. 2025: doi: 10.29328/journal.ijpra.1001107; 8: 017-023
-
Phytochemical Compounds and the Antifungal Activity of Centaurium pulchellum Ethanol Extracts in IraqNoor Jawad Khadhum, Neepal Imtair Al-Garaawi*, Antethar Jabbar Al-Edani. Phytochemical Compounds and the Antifungal Activity of Centaurium pulchellum Ethanol Extracts in Iraq. J Plant Sci Phytopathol. 2024: doi: 10.29328/journal.jpsp.1001137; 8: 079-083
Most Viewed
-
Evaluation of Biostimulants Based on Recovered Protein Hydrolysates from Animal By-products as Plant Growth EnhancersH Pérez-Aguilar*, M Lacruz-Asaro, F Arán-Ais. Evaluation of Biostimulants Based on Recovered Protein Hydrolysates from Animal By-products as Plant Growth Enhancers. J Plant Sci Phytopathol. 2023 doi: 10.29328/journal.jpsp.1001104; 7: 042-047
-
Sinonasal Myxoma Extending into the Orbit in a 4-Year Old: A Case PresentationJulian A Purrinos*, Ramzi Younis. Sinonasal Myxoma Extending into the Orbit in a 4-Year Old: A Case Presentation. Arch Case Rep. 2024 doi: 10.29328/journal.acr.1001099; 8: 075-077
-
Feasibility study of magnetic sensing for detecting single-neuron action potentialsDenis Tonini,Kai Wu,Renata Saha,Jian-Ping Wang*. Feasibility study of magnetic sensing for detecting single-neuron action potentials. Ann Biomed Sci Eng. 2022 doi: 10.29328/journal.abse.1001018; 6: 019-029
-
Pediatric Dysgerminoma: Unveiling a Rare Ovarian TumorFaten Limaiem*, Khalil Saffar, Ahmed Halouani. Pediatric Dysgerminoma: Unveiling a Rare Ovarian Tumor. Arch Case Rep. 2024 doi: 10.29328/journal.acr.1001087; 8: 010-013
-
Physical activity can change the physiological and psychological circumstances during COVID-19 pandemic: A narrative reviewKhashayar Maroufi*. Physical activity can change the physiological and psychological circumstances during COVID-19 pandemic: A narrative review. J Sports Med Ther. 2021 doi: 10.29328/journal.jsmt.1001051; 6: 001-007

HSPI: We're glad you're here. Please click "create a new Query" if you are a new visitor to our website and need further information from us.
If you are already a member of our network and need to keep track of any developments regarding a question you have already submitted, click "take me to my Query."