Quantum analysis of sub harmonic generation with two-mode coherent light

In this work the statistical and squeezing properties of light-driven by sub-harmonic generation with two-mode coherent light are studied. With interaction Hamiltonian of both two-mode coherent and sub harmonic generation, we have driven master equation of system under consideration. From the master equation, the solution of the C-number Langevin equation is derived. It helps us to solve quadrature variance, quadrature squeezing, mean, and variance of photon number for light produced by sub-harmonic generation with the two-mode coherent light state. And the result shows that; the squeezing occurs in plus quadrature with the maximum squeezing of 87%. The photon statistics of the system under consideration is subpoissonian in which both mean & variance are increasing as kappa increase.

In quantum theory, light is made up of particles called photons. And the quantum properties of light are determined by the quantum state of light using creation and annihilation operators. Some of them are coherent state, chaotic state, squeezed state, and number state. From the all-quantum states of light, coherent states are the most important and frequently arise in quantum optics. Which is defined in terms of displacement operator, and it is an Eigen state of annihilation operator. Which can satisfy properties like completeness, the variance of photon number is equal to mean photon number, and it is not orthogonal [1-6]. The sub-harmonic generator is and well characterized optical devices in quantum optics. In which, a pump photon interacts with a nonlinear crystal inside a cavity and is down-converted into two highly correlated photons. If these photons have the same frequency, the device is called a single-mode sub-harmonic generator; otherwise, it is called a two-mode sub-harmonic generator [2,6-9].

The squeezing and statistical properties of light produced by sub-harmonic generation with the different quantum states of light have been investigates by several authors [10-14]. For sub-harmonic generation with first-order Hamiltonian, the mean photon number for signal-signal and signal idler modes are the same, and the maximum global quadrature squeezing of signal-signal or signal idler mode is 50% below vacuum-state level. In the interaction of sub-harmonic generation is with parametric amplification, the nonclassical properties and multi-mode process are investigates in a sprit of Mandel-Rice photon count formula.

In this work the statistical and squeezing properties of light produced by sub-harmonic generation with the two-mode coherent state. With the solution of the C-number Langevin equation in normal ordering, the quadretuare variance, quadrature squeezing, and photon statistics of the system is analyzed.

Master equation

Under this section, we want to determine the interaction Hamiltonian of two-mode sub-harmonic generation coupled to a two-mode coherent state. The interaction Hamiltonian of the two-mode coherent state is given by;

$\begin{array}{l}\frac{d}{dt}<a^2(t)\ge =\epsilon -\frac{k}{2}<a^2(t)>-2\lambda a(t){\beta }^{\ast }(t)>+2\epsilon <a(t)>+\\ <a(t)f_a(t)>+<f_a(t)>+\frac{k}{2}(2\stackrel{⌢}{a}\stackrel{⌢}{\rho }{\stackrel{⌢}{a}}^{+}-{\stackrel{⌢}{a}}^{+}\stackrel{⌢}{a}\stackrel{⌢}{\rho }-\stackrel{⌢}{\rho }{\stackrel{⌢}{a}}^{+}\stackrel{⌢}{a})\\ +\frac{k}{2}(2\stackrel{⌢}{b}\stackrel{⌢}{\rho }{\stackrel{⌢}{b}}^{+}-{\stackrel{⌢}{b}}^{+}\stackrel{⌢}{b}\stackrel{⌢}{\rho }-\stackrel{⌢}{\rho }{\stackrel{⌢}{b}}^{+}\stackrel{⌢}{b})(f_a(t)\&f_b)V_4=-<\stackrel{⌢}{a}>\\ \stackrel{⌢}{a}\to a,{\stackrel{⌢}{a}}^{+}\to a\ast ,{\stackrel{⌢}{b}}^{+}\to \beta \ast \text{ and }\stackrel{⌢}{b}\to \beta \end{array}$ (1)

And the interaction Hamiltonian of two-mode sub-harmonic generation is given as;

$\stackrel{⌢}{H}=i\lambda (\stackrel{⌢}{a}\stackrel{⌢}{b}\stackrel{⌢}{p}-{\stackrel{⌢}{a}}^{+}{\stackrel{⌢}{b}}^{+})$ (2)

Using Eqs. (1) and (2) we can put the interaction Hamiltonian for two-mode sub-harmonic generation coupled to two-mode coherent state in the form of;

$\stackrel{⌢}{H}=i\epsilon ({\stackrel{⌢}{a}}^{+}-\stackrel{⌢}{a}+{\stackrel{⌢}{b}}^{+}-\stackrel{⌢}{b})+i\lambda (\stackrel{⌢}{a}\stackrel{⌢}{b}\stackrel{⌢}{p}-{\stackrel{⌢}{a}}^{+}{\stackrel{⌢}{b}}^{+})$ (3)

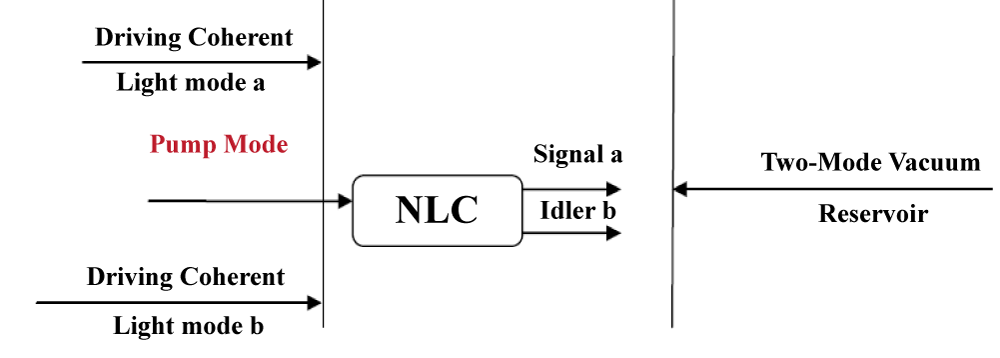
The diagrammatical description of the system is put as (Figure 1).

Here we seek to find the equation of evolution of reduced density operator for cavity mode light produced by sub-harmonic generation with two-mode coherent light. Then the master equation for subharmonic generation with two-mode coherent state coupled to vacuum reservoir can putt as [8].

$\begin{array}{l}\frac{d\stackrel{⌢}{\rho }}{dt}=-i\left[\stackrel{⌢}{H},\stackrel{⌢}{\rho }\right]+\frac{k}{2}\left(2\stackrel{⌢}{a}\stackrel{⌢}{\rho }{\stackrel{⌢}{a}}^{+}-{\stackrel{⌢}{a}}^{+}\stackrel{⌢}{a}\stackrel{⌢}{\rho }-\stackrel{⌢}{\rho }{\stackrel{⌢}{a}}^{+}\stackrel{⌢}{a}\right)\\ +\frac{k}{2}\left(2\stackrel{⌢}{b}\stackrel{⌢}{\rho }{\stackrel{⌢}{b}}^{+}-{\stackrel{⌢}{b}}^{+}\stackrel{⌢}{b}\stackrel{⌢}{\rho }-\stackrel{⌢}{\rho }{\stackrel{⌢}{b}}^{+}\stackrel{⌢}{b}\right)\end{array}$ (4)

where k and $\stackrel{⌢}{\rho }$ is cavity damping constant and density operator respectively. Using Eq. (3) into Eq. (4), we easily get

$V_3\left(2\stackrel{⌢}{a}\stackrel{⌢}{\rho }{\stackrel{⌢}{a}}^{+}\stackrel{⌢}{a}-{\stackrel{⌢}{a}}^{+}\stackrel{⌢}{a}\stackrel{⌢}{\rho }\stackrel{⌢}{a}-\stackrel{⌢}{\rho }{\stackrel{⌢}{a}}^{+}{\stackrel{⌢}{a}}^2\right)$ (5)

Eq. (5) is called as the master equation for two-mode sub-harmonic generation with two-mode coherent light.

C-number langevin

Under this section, we seek to find c-number Langevin equation with the help of master equation. The time evolution operator in the Schrödinger picture can be put as

$\frac{d}{dt}<\stackrel{⌢}{a}\left(t\right)>=\text{Tr}\left(\frac{d\stackrel{⌢}{\rho }}{dt}\stackrel{⌢}{a}\left(t\right)\right)$ (6)

Substituting Eq. (5) into Eq. (6) we find

$\begin{array}{l}\frac{d}{dt}<\stackrel{⌢}{a}\left(t\right)>=\epsilon \text{Tr}({\stackrel{⌢}{a}}^{+}\stackrel{⌢}{\rho }\stackrel{⌢}{a}+{\stackrel{⌢}{b}}^{+}\stackrel{⌢}{\rho }\stackrel{⌢}{a}-\stackrel{⌢}{a}\stackrel{⌢}{\rho }\stackrel{⌢}{a})\\ -\stackrel{⌢}{\rho }\stackrel{⌢}{a}\stackrel{⌢}{b}-\stackrel{⌢}{\rho }{\stackrel{⌢}{a}}^{+}\stackrel{⌢}{a}-\stackrel{⌢}{\rho }{\stackrel{⌢}{b}}^{+}\stackrel{⌢}{a}+\stackrel{⌢}{\rho }{\stackrel{⌢}{a}}^{+}+\stackrel{⌢}{\rho }\stackrel{⌢}{b}\stackrel{⌢}{a}\\ \lambda (\stackrel{⌢}{a}\stackrel{⌢}{b}\stackrel{⌢}{\rho }\stackrel{⌢}{a}-{\stackrel{⌢}{a}}^{+}{\stackrel{⌢}{b}}^{+}\stackrel{⌢}{\rho }\stackrel{⌢}{a}-\stackrel{⌢}{\rho }\stackrel{⌢}{a}\stackrel{⌢}{b}\stackrel{⌢}{a}\stackrel{⌢}{\rho }\stackrel{⌢}{a}+{\stackrel{⌢}{b}}^{+}\stackrel{⌢}{a})\\ +\frac{k}{2}(2\stackrel{⌢}{a}\stackrel{⌢}{\rho }{\stackrel{⌢}{a}}^{+}\stackrel{⌢}{a}-{\stackrel{⌢}{a}}^{+}\stackrel{⌢}{a}\stackrel{⌢}{\rho }\stackrel{⌢}{a}-\stackrel{⌢}{\rho }{\stackrel{⌢}{a}}^{+}{\stackrel{⌢}{a}}^2)\\ \frac{k}{2}(2\stackrel{⌢}{b}\stackrel{⌢}{\rho }{\stackrel{⌢}{b}}^{+}\stackrel{⌢}{a}-{\stackrel{⌢}{b}}^{+}\stackrel{⌢}{b}\stackrel{⌢}{\rho }\stackrel{⌢}{a}-\stackrel{⌢}{\rho }{\stackrel{⌢}{b}}^{+}\stackrel{⌢}{b}\stackrel{⌢}{a})\end{array}$ (7)

Or we can write this equation in short hand form as

$\frac{d}{dt}<\stackrel{⌢}{a}\left(t\right)>=\text{ε}{V}_1+ \lambda V_2+\frac{k}{2}\left(V_3+V_4\right)$ (8)

In which

$V_1=\text{Tr(}{\stackrel{⌢}{a}}^{+}\stackrel{⌢}{\rho }\stackrel{⌢}{a}+{\stackrel{⌢}{b}}^{+}\stackrel{⌢}{\rho }\stackrel{⌢}{a}-\stackrel{⌢}{a}\stackrel{⌢}{\rho }\stackrel{⌢}{a}-\stackrel{⌢}{b}\stackrel{⌢}{\rho }\stackrel{⌢}{a}-\stackrel{⌢}{\rho }{\stackrel{⌢}{a}}^{+}\stackrel{⌢}{a}+\stackrel{⌢}{\rho }{\stackrel{⌢}{a}}^2\text{+}\stackrel{⌢}{\rho }\stackrel{⌢}{b}\stackrel{⌢}{a}\text{)}$ (9)

$V_2=\text{(}\stackrel{⌢}{a}\stackrel{⌢}{b}\stackrel{⌢}{\rho }\stackrel{⌢}{a}+{\stackrel{⌢}{a}}^{+}{\stackrel{⌢}{b}}^{+}\stackrel{⌢}{\rho }\stackrel{⌢}{a}-\stackrel{⌢}{\rho }\stackrel{⌢}{a}\stackrel{⌢}{b}\stackrel{⌢}{a}+\stackrel{⌢}{\rho }{\stackrel{⌢}{a}}^{+}{\stackrel{⌢}{b}}^{+}\stackrel{⌢}{a}\text{)}$ (10)

$V_3\left(2\stackrel{⌢}{a}\stackrel{⌢}{\rho }{\stackrel{⌢}{a}}^{+}\stackrel{⌢}{a}-{\stackrel{⌢}{a}}^{+}\stackrel{⌢}{a}\stackrel{⌢}{\rho }\stackrel{⌢}{a}-\stackrel{⌢}{\rho }{\stackrel{⌢}{a}}^{+}{\stackrel{⌢}{a}}^2\right)$ (11)

And

$V_4=\text{(}2\stackrel{⌢}{b}\stackrel{⌢}{\rho }{\stackrel{⌢}{b}}^{+}\stackrel{⌢}{a}-{\stackrel{⌢}{b}}^{+}\stackrel{⌢}{b}\stackrel{⌢}{\rho }\stackrel{⌢}{a}-\stackrel{⌢}{\rho }{\stackrel{⌢}{b}}^{+}\stackrel{⌢}{b}\stackrel{⌢}{a})$ (12)

Applying the cyclic properties of trace operator with commutation relation and rearranging in normal order form we can re set Eq. (9) as,

$V_1=\text{Tr(}\stackrel{⌢}{\rho }\stackrel{⌢}{a}{\stackrel{⌢}{a}}^{+}+\stackrel{⌢}{\rho }\stackrel{⌢}{a}{\stackrel{⌢}{b}}^{+}-\stackrel{⌢}{\rho }{\stackrel{⌢}{a}}^2-\stackrel{⌢}{\rho }\stackrel{⌢}{a}\stackrel{⌢}{b}-\stackrel{⌢}{\rho }{\stackrel{⌢}{a}}^{+}\stackrel{⌢}{a}-\stackrel{⌢}{\rho }{\stackrel{⌢}{b}}^{+}\stackrel{⌢}{a})$ (13)

Or

$=\text{Tr(}\stackrel{⌢}{\rho }[\stackrel{⌢}{a},{\stackrel{⌢}{a}}^{+}]+\stackrel{⌢}{\rho }[\stackrel{⌢}{a},{\stackrel{⌢}{b}}^{+}]-\stackrel{⌢}{\rho }[\stackrel{⌢}{a},\stackrel{⌢}{b}]\text{)}$ (14)

This can be simplified as

$V_1=\text{Tr(}\stackrel{⌢}{\rho })=1$ (15)

Where

$[\stackrel{⌢}{a},{\stackrel{⌢}{a}}^{+}]=1]\text{)}$ (16)

$[\stackrel{⌢}{a},{\stackrel{⌢}{b}}^{+}]=[\stackrel{⌢}{a},\stackrel{⌢}{b}]=0]$ (17)

We easily get

$V_2=-<{\stackrel{⌢}{b}}^{+}>$ (18)

$V_3=-<\stackrel{⌢}{a}>$ (19)

V₄ = 0 (20)

With help of Eqs. (15), (18), (19) and Eq. (20) we can put Eq. (8) in the form of

$\frac{d}{dt}<\stackrel{⌢}{a}(t)>=\epsilon -\lambda <{\stackrel{⌢}{b}}^{+}(t)>-\frac{k}{2}<\stackrel{⌢}{a}(t)>$ (21)

Replacing the operator by c number as and adding notice force (fα(t) & fb(t)) in which

==0 (22)

Then the above equation takes the form

$\frac{d}{dt}<a(t)>=\epsilon -\lambda <{\beta }^{\ast }(t)>-\frac{k}{2}<\alpha (t)>+f_a(t)$ (23)

Following the same procedure we have

$\frac{d}{dt}<a^{\ast }(t)>=\epsilon -<a^{\ast }(t)>-<\beta (t)>+f_a{}^{\ast }(t)$ (24)

${(\Delta n)}^2=\frac{32{\epsilon }^2}{{\gamma }_{\pm }^2}(\frac{4{\epsilon }^2}{{\gamma }_{+}^2}-\frac{\gamma }{2{\gamma }_{+}}+\frac{\gamma }{2{\gamma }_{-}})+\text{4}{(\frac{4{\epsilon }^2}{{\gamma }_{+}^2}-\frac{\gamma }{2{\gamma }_{+}}+\frac{\gamma }{2{\gamma }_{-}})}^2+\frac{192{\epsilon }^4}{{\gamma }_{+}^4}+\frac{64{\epsilon }^2}{{\gamma }_{\pm }^2}+8{\stackrel{-}{n}}_1^2+\overline{n}-{\overline{n}}^2$ (25)

$\frac{d}{dt}<{\alpha }^{*}\left(t\right)\alpha \left(t\right)>=-k<{\alpha }^{*}(t)?(t)>-\lambda \left(<\alpha \left(t\right)\beta \left(\text{t}\right)>+<{\alpha }^{*}\left(t\right){\beta }^{*}\left(\text{t}\right)>\right)$

$\begin{array}{l}\frac{d}{dt}<{\alpha }^{*}\left(t\right)\alpha \left(t\right)>=-k<{\alpha }^{*}(t)?(t)>-\lambda \left(<\alpha \left(t\right)\beta \left(\text{t}\right)>+<{\alpha }^{*}\left(t\right){\beta }^{*}\left(\text{t}\right)>\right)\\ +\text{ ε}\left(\begin{array}{c}<{\alpha }^{*}\left(t\right)>+<{\beta }^{*}\left(\text{t}\right)\\ +<{\alpha }^{*}\left(t\right)f_a\left(\text{t}\right)>+<f_a{}^{*}\left(\text{t}\right)\alpha \left(t\right)>\end{array}\right)\end{array}$ (26)

and

$\begin{array}{l}\frac{d}{dt}<\alpha \left(t\right)\beta \left(\text{t}\right)>=\text{k}<\alpha \left(t\right)\beta \left(\text{t}\right)>- \lambda \left(<{\alpha }^{*}\left(t\right)\alpha \left(t\right)>- \lambda <{\beta }^{*}\left(\text{t}\right)\beta \left(\text{t}\right)>\right)\\ +\text{ε}\left(<\beta \left(\text{t}\right)>+<\alpha \left(t\right)>\right)- \lambda \end{array}$ (27)

The solution of Eq. (24) can be takes the form of

$\alpha \left(t\right)=\alpha \left(0\right)e^{\frac{-kt}{2}}+\left({\displaystyle {\int }_{\text{0}}^{t}e}\right)e^{\frac{-k\left(t-\dot{t}\right)}{2}}\left(f_a\left(\dot{t}\right)+\text{ε}-\lambda {\beta }^{*}\left(\dot{t}\right)\right)d\stackrel{`}{t},$ (28)

After applying some mathematical procedure we can set

$\alpha \left(t\right)=E_{+}\left(t\right)\alpha \left(0\right)+E_{\_}\left(t\right){\beta }^{*}\left(0\right)+F_{+}\left(t\right)+F_{-}\left(t\right)$ (29)

Similarly we have

$\beta \left(t\right)=E_{+}\left(t\right)\beta \left(0\right)+E_{\_}\left(t\right){\alpha }^{*}\left(0\right)+F_{+}{}^{*}\left(t\right)+F_{-}{}^{*}\left(t\right)$ (30)

Where

$E_{\pm }\left(t\right)=\frac{1}{2}\left(e^{\frac{-{\gamma }_{+}t}{2}}\pm e^{\frac{-{\gamma }_{+}t}{2}}\right)$ (31)

And

$F_{\pm }\left(t\right)\frac{1}{2}{\left({\displaystyle {\int }_{\text{0}}^{t}e}\right)}^{\frac{-{\gamma }_{+}\left(t-t^{\text{'} }\right)}{ 2} [ \epsilon \pm \epsilon +f_a\left(\stackrel{`}{t}\right)\pm f_b{}^{*}\left(\text{t}\right) ]}d{t}^{\text{'} }$ (32)

Quadrature variance

The squeezing properties of two-mode cavity light can be given by plus and minus quadrature as

${\stackrel{⌢}{a}}_{\pm }=\sqrt{\pm ({\stackrel{⌢}{a}}^{+}\text{+ }\stackrel{⌢}{a})}$ (33)

The two-mode light is said to be in a squeezed state if $\Delta {\stackrel{⌢}{a}}_{+}\le \sqrt{2}$ and $\Delta {\stackrel{⌢}{a}}_{-}\ge \sqrt{2}$ with $\Delta {\stackrel{⌢}{a}}_{+}\Delta {\stackrel{⌢}{a}}_{-}\ge 2$ . Then the variance can be calculated as,

${\left(\Delta C_{\pm }\left(t\right)\right)}^2=<{\stackrel{⌢}{a}}_{\pm }{}^2(t)>-{\stackrel{⌢}{a}}_{\pm }(t){>}^2$ (34)

With the help of Eq. (34) and arranging the Eq. (35) in normal order fashion, we gate

$\begin{array}{l}{\left(\Delta C_{\pm }\left(t\right)\right)}^2=2\pm <{\stackrel{⌢}{a}}_{\pm }{}^{+2}\left(t\right)>+<{\stackrel{⌢}{a}}_{\pm }{}^2>\\ \pm 2<{\stackrel{⌢}{a}}_{\pm }{}^{+}\left(t\right){\hat{a}}_{\pm }\left(t\right) \mp \left(<{\stackrel{⌢}{a}}_{\pm }{}^{+}\left(t\right)>\pm <{\stackrel{⌢}{a}}_{\pm }\left(t\right){>}^2\right)\end{array}$ (35)

Changing the operators into a C-number variable, we can set the above equation as,

${\left(\Delta C_{\pm }\left(t\right)\right)}^2=2\pm \left(\begin{array}{c}<{\lambda }_{\pm }{}^2\left(t\right)\\ -<{\lambda }_{\pm }\left(t\right){>}^2\end{array}\right).$ (36)

Where

${\lambda }_{\pm }={\lambda }^{*}\left(t\right)\pm \lambda$ (37)

and

$\lambda =\alpha +\beta$ (38)

Finally, we can express the differentiation form of terms in Eq. (36) as

$\frac{d{\lambda }_{\pm }(t)}{dt}=-\frac{1}{2}{\gamma }_{\pm }{\lambda }_{\pm }\left(t\right)+2\left(\epsilon +\epsilon \right)+f_a{}^{*}\left(\text{t}\right)\pm f_a\left(t\right)+f_b{}^{*}\left(\text{t}\right)\pm f_b\left(t\right)$ (39)

The solution for the above equation takes the form

$\begin{array}{l}{\lambda }_{\pm }\left(t\right)={\lambda }_{\pm }\left(0\right)e^{\frac{-{\gamma }_{+}t}{2}}+{{\displaystyle {\int }_0^{t}e}}^{\frac{-{\gamma }_{+}(t-t^{\text{'}})}{2}}\\ \left[2\left(\epsilon \pm \epsilon \right)+f_a{}^{*}\left(t^{\text{'}}\right)\pm f_a\left(t^{\text{'}}\right)+f_b{}^{*}(t^{\text{'}})\pm f_b(t^{\text{'}})\right]d{t}^{\text{'}}\end{array}$ (40)

Carrying out integration wrt and taking out both side under expectation value then we have

$<{\lambda }_{\pm }\left(t\right)>=<{\lambda }_{\pm }\left(0\right)>e^{\frac{-{\gamma }_{+}t}{2}}+\frac{4}{{\gamma }_{\pm }}\left(\epsilon \pm \epsilon \right)\left(1-e^{\frac{-{\gamma }_{+}t}{2}}\right)$ (41)

With similar procedure we find

$\begin{array}{l}<{\lambda }_{\pm }{}^2\left(t\right)>=<{\lambda }_{\pm }{}^2\left(0\right)>e^{-{\gamma }_{+}t}+\frac{8}{{\lambda }_{\pm }}(\epsilon \pm \epsilon )<{\lambda }_{\pm }\left(0\right)>(e^{\frac{-{\gamma }_{+}t}{2}}-e^{-{\gamma }_{+}t}\\ +\frac{16}{{\gamma }_{\pm }{}^2}{\left(\epsilon \pm \epsilon \right)}^2\left(1-2e^{\frac{-{\gamma }_{+}t}{2}}+e^{-{\gamma }_{+}t}\right)-\frac{4\gamma }{{\gamma }_{\pm }}\left(1-e^{-{\gamma }_{+}t}\right)\end{array}$ (42)

Using Eq. (42) and (43) into Eq. (37) the quadretuare variance for system under consideration takes the form

${\left(\Delta C_{\pm }\left(t\right)\right)}^2=2\mp \frac{4\gamma }{k+2\gamma }.$ (43)

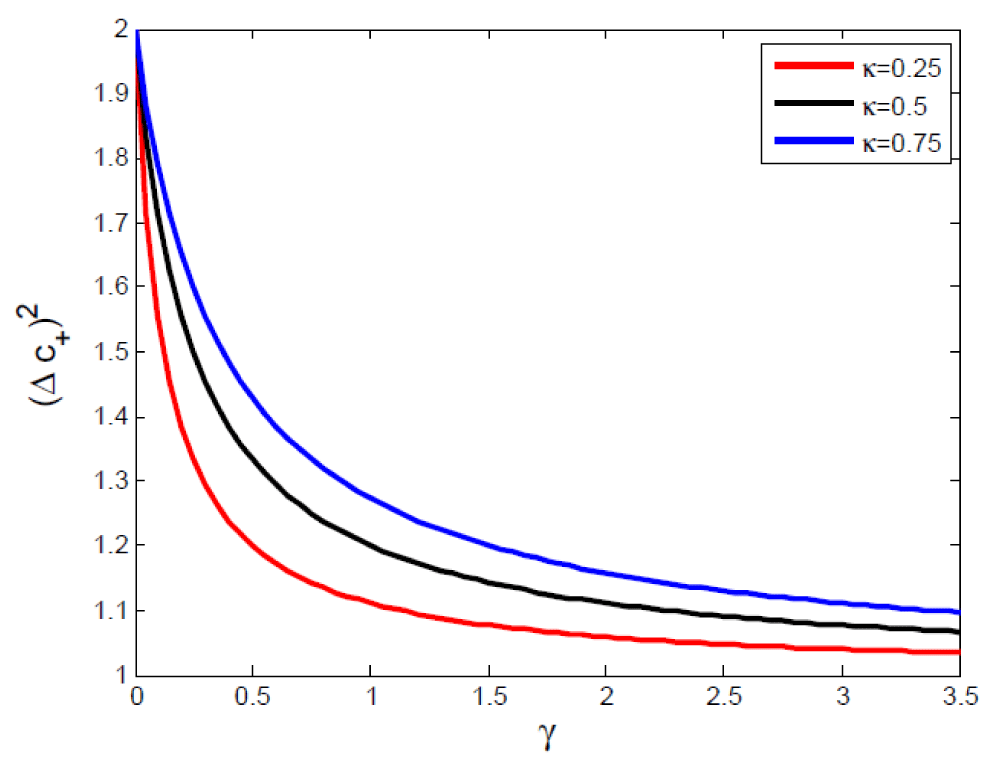
From Eq. (43) and above figure, one can determine that the two- mode sub-harmonic generation with to two-mode coherent light is in a squeezed state and the Squeezing occurs in the plus quadretuare. And quadrature variance decrease as γ increase but, mean variance increase as kappa increase (Figure 2).

Quadrature squeezing

Here we calculate quadretuare squeezing with help of quadretuare variance which is given by

$\text{S}=\frac{{({\stackrel{⌢}{a}}_{\pm }\left(t\right))}_v{}^2-{\stackrel{⌢}{a}}_{\pm }{\left(t\right)}^2}{{({\stackrel{⌢}{a}}_{\pm }\left(t\right))}_v{}^2}.$ (44)

Where

${({\stackrel{⌢}{a}}_{\pm }\left(t\right))}_v{}^2=2$ (45)

With the help of Eq. (45) and Eq. (43) we can set quadrature squeezing as

$\text{S}=\frac{2\gamma }{k+2\gamma }$ (46)

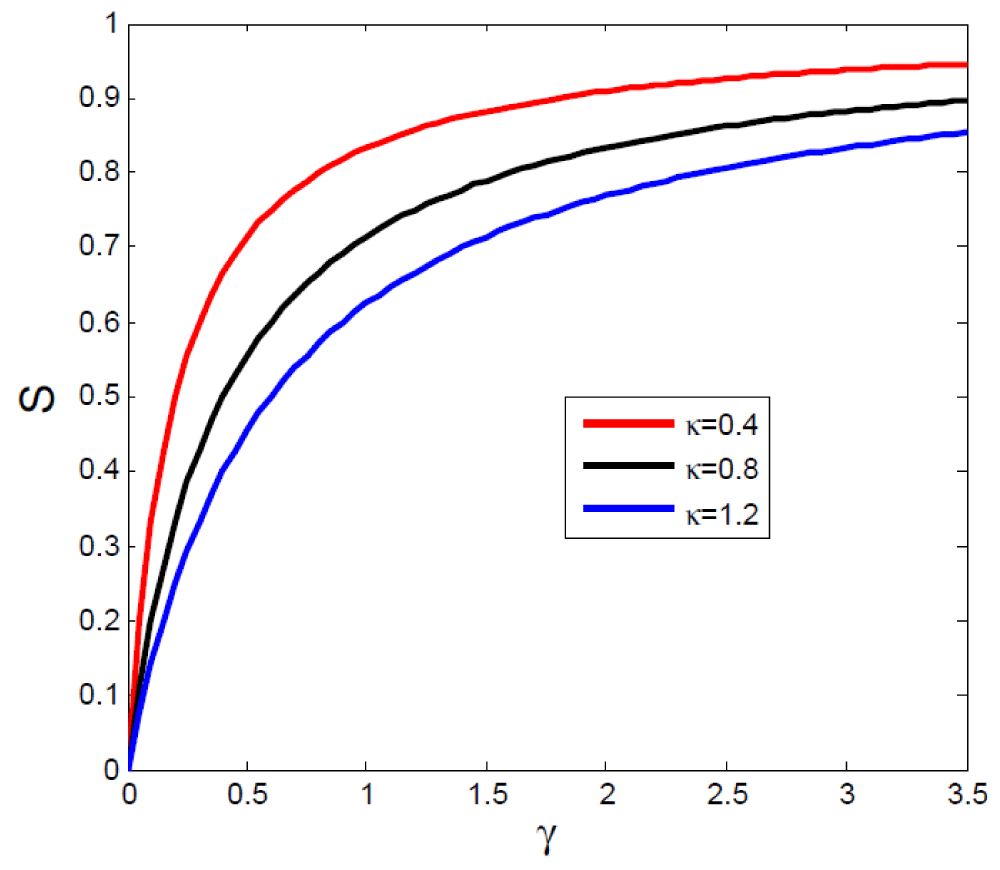
Figure 3 shows that quardature squeezing is inversely proportional with kappa and direct proportion to gamma. The less amount of kappa means the more squeezing occurs in the system.

Photon statistics

The statistical properties of cavity light produced by two-mode sub-harmonic generation coupled to coherent light are solved by applying a C-number Langevin equation. Here we calculate the mean photon number and variance of photon number.

Mean photon number

The mean photon number for two-mode light is given as;

${\stackrel{⌢}{n}}_1=<{\alpha }^{*}\left(t\right)\alpha \left(t\right)>$ (47)

Where

${\stackrel{⌢}{n}}_1=<{\alpha }^{*}\left(t\right)\alpha \left(t\right)>$ (48)

$\begin{array}{l}=<F_{+}{}^{*}\left(t\right)F_{+}\left(t\right)>+<F_{+}{}^{*}\left(t\right)F_{-}\left(t\right)>+\\ <F_{-}{}^{*}\left(t\right)F_{+}\left(t\right)>+<F_{-}{}^{*}\left(t\right)F_{-}\left(t\right)>\end{array}$ (49)

On account of Eq. (32) all expectation values can be calculated as

$<F_{+}{}^{*}\left(t\right)F_{+}\left(t\right)>=\frac{4e^2}{{\gamma }_{+}^2}(\text{1}-\text{2}{e}^{\frac{-{\gamma }_{+}t}{2}}+e^{-{\gamma }_{+}t})-\frac{\gamma }{2{\gamma }_{+}^2}\left(1-e^{-{\gamma }_{+}t}\right)$ (50)

$<F_{-}{}^{*}\left(t\right)F_{-}\left(t\right)> =\frac{\gamma }{2{\gamma }_{-}}(1-e^{-{\gamma }_{-}t})$ (51)

and

$<F_{+}{}^{*}\left(t\right)F_{-}\left(t\right)>=<F_{-}{}^{*}\left(t\right)F_{+}\left(t\right)>=0$ (52)

Using Eq. (50), (51) and (52) into Eq. (49) we can set the mean photon number for single-mode as

${\overline{n}}_1=\frac{4{\epsilon }^2}{{\left(k+2\gamma \right)}^2}+\frac{2{\gamma }^2}{k^2-4{\gamma }^2}.$ (53)

Similarly

${\overline{n}}_2=\frac{4{\epsilon }^2}{{\left(k+2\gamma \right)}^2}+\frac{2{\gamma }^2}{k^2-4{\gamma }^2}.$ (54)

With help of Eq. (53) and (54) Eq. (47) takes the form

$\overline{n}=\frac{8{\epsilon }^2}{{\left(k+2\gamma \right)}^2}+\frac{4{\gamma }^2}{k^2-4{\gamma }^2}.$ (55)

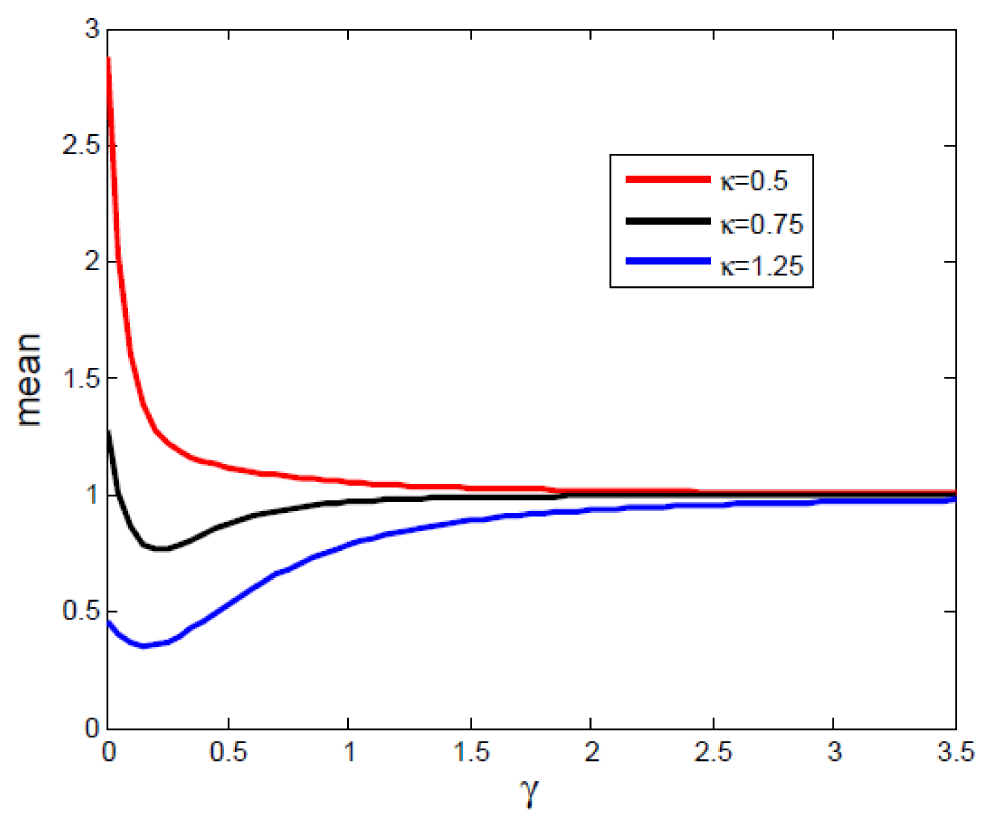
From Eq. (53)-(55) we can determine that the mean photon number for two-mode light is the sum individual mean photon number of single-mode lights. And Figure 4 shows the dependence of mean photon number on kappa, as kappa increase the mean photon number for system under consideration decreases.

Variance of photon number

The variance of two-mode light takes the form

${(\Delta n_s)}^2=<{\gamma }^{*2}{\gamma }^2>+\overline{n}-{\overline{n}}^2$ (56)

The only unknown term is

$\begin{array}{l}<{\gamma }^{*2}{\gamma }^2> =<{\alpha }^{*2}{\alpha }^2>+<{\beta }^{*2}{\beta }^2> +<{\alpha }^{*2}{\beta }^{*2}>+2<{\alpha }^{*2}\alpha \beta >\\ +<{\alpha }^2{\beta }^{*2}>+2<\alpha {\beta }^{*2}\beta >+2<{\alpha }^{*}{\alpha }^2{\beta }^{*}>+2<{\alpha }^{*}{\beta }^{*}{\beta }^2> +4<{\alpha }^{*}\alpha {\beta }^{*}\beta >\end{array}$ (57)

where

$<{\alpha }^{*2}{\alpha }^2>=\frac{16{\epsilon }^4}{{\gamma }_{+}^4}+2{\stackrel{-}{n}}_1^2.$ (58)

$<{\beta }^{*2}{\beta }^2> = \frac{16{\epsilon }^4}{{\gamma }_{+}^4}+2{\stackrel{-}{n}}_2^2.$ (59)

$<{\alpha }^{*2}{\beta }^{*2}> = \frac{48{\epsilon }^4}{{\gamma }_{+}^4}.$ (60)

$2<{\alpha }^{*2}\alpha \beta > = \frac{8{\epsilon }^2}{{\gamma }_{+}^2}(\frac{4{\epsilon }^2}{{\gamma }_{+}^2}-\frac{\gamma }{2{\gamma }_{+}}+\frac{\gamma }{2{\gamma }_{-}})+\frac{16{\epsilon }^2}{{\gamma }_{+}^2}{\stackrel{-}{n}}_1$ (61)

$2<\alpha {\beta }^{*2}\beta > = \frac{8{\epsilon }^2}{{\gamma }_{+}^2}(\frac{4{\epsilon }^2}{{\gamma }_{+}^2}-\frac{\gamma }{2{\gamma }_{+}}+\frac{\gamma }{2{\gamma }_{-}})+\frac{16{\epsilon }^2}{{\gamma }_{+}^2}{\stackrel{-}{n}}_2$ (62)

And

$4<{\alpha }^{*}\alpha {\beta }^{*}\beta > =4(\frac{4{\epsilon }^2}{{\gamma }_{+}^2}-\frac{\gamma }{2{\gamma }_{+}}+\frac{\gamma }{2{\gamma }_{-}})+\frac{64{\epsilon }^4}{{\gamma }_{+}^4}+4{\stackrel{-}{n}}_1^2$ (63)

Using Eqs. (58), (59), (60), (61), (62) and Eq. (63) into Eq. (57) we have

$\begin{array}{l}<{\lambda }^{*2}{\lambda }^2> =\frac{32{\epsilon }^2}{{\gamma }_{\pm }^2}(\frac{4{\epsilon }^2}{{\gamma }_{+}^2}-\frac{\gamma }{2{\gamma }_{+}}+\frac{\gamma }{2{\gamma }_{-}})+\text{ 4}{(}^{\frac{4{\epsilon }^2}{{\gamma }_{+}^2}}\\ +\frac{192{\epsilon }^4}{{\gamma }_{+}^4}+\frac{64{\epsilon }^2{\stackrel{-}{n}}_1}{{\gamma }_{\pm }^2}+8{\stackrel{-}{n}}_1^2\end{array}$ (64)

On account of Eq. (65), Eq. (57) takes the form

$\begin{array}{l}{(}^{\Delta }=\frac{32{\epsilon }^2}{{\gamma }_{\pm }^2}(\frac{4{\epsilon }^2}{{\gamma }_{+}^2}-\frac{\gamma }{2{\gamma }_{+}}+\frac{\gamma }{2{\gamma }_{-}})+\text{4}{(}^{\frac{4{\epsilon }^2}{{\gamma }_{+}^2}}\\ +\frac{192{\epsilon }^4}{{\gamma }_{+}^4}+\frac{64{\epsilon }^2}{{\gamma }_{\pm }^2}+8{\stackrel{-}{n}}_1^2+\overline{n}-{\overline{n}}^2\end{array}$ (65)

Eq. (65) is called as the variance of photon number for two- mode sub-harmonic generation coupled to two-mode coherent light.

In this work, we considered the cavity mode produced by a two-mode sub-harmonic generation with two-mode coherent light. With the help of interaction Hamiltonian, we have obtained a master equation, which helps as to find C-number Langevin equation. With C-number Langevin equation we have determined quadrature variance, quadrature squeezing and the photon statistics of the system. The result shows the mean photon number and variance of photon are decrease as kappa increases, but the variance and quadrature squeezing are increase with kappa increase. The variance of photon number is greater than mean photon number, the squeezing occurs in plus quadrature, quadrature variance is decrease as γ increase but, quadrature squeezing is the opposite of quadretuare variance and the maximum squeezing is 87% for γ = 1 and k = 0.3.

1. El-Orany FAA, Obada ASF, Abdelslam MA, Wahiddin MRB. Evolution of the pair-coherent state with the two-qubit: entanglement and cat-state generation. J Modern Optics. 2008; 55: 1649-1666.
2. Kefelegn G. Superposition of two-level laser light Beams. MSc Thesis. 2013.
3. Ayalew A, Kassahun F. Superposed Two mode chaotic, coherent, and Squeezed Vacuum State. Aksum University and Addis Ababa University. 2014.
4. Kassahun F. Fundamentals of Quantum Optics. Lulu, North Carolina. 2008.
5. Grynberg G, Aspect A, Fabre C. Introduction to quantum optics: from the semi-classical approach to quantized light. Cambridge University Press. 2010.
6. Hailu L. Dynamics of coherently driven nondegenerate three-level atom. MSc Thesis. Addis Ababa University. 2013.
7. Getahun S, Chibssa G, Abedella S, Mossisa M, Nuri M. CV Entanglement Analysis in the Superposition of Sub-harmonic and Second Harmonic Generation of Light with Injected Squeezed Laser Beams. Global J Sci Front Res. A Physics and Space Science.2003; 7: 2003.
8. Melaku M, Hirpo D. Entanglement of Cavity Light Produced by a Superposed Two-Mode Coherent and Sub-harmonic Light. arXiv: 1904.06060v1 [quant-ph] 12 Apr 2019.
9. Tewodros Y, Fesseha K. Coherently driven degenerate three-level laser with parametric amplifier. PMC Physics. 2010; 3.
10. Fisseha K. Quantum analysis of subharmonic generation via first-order Hamiltonian. arxiv 1508.00340v1[quant.ph]. 2015.
11. Bajar J. Photon statistics of higher harmonics & sub harmonic generation. J Eur Optical Soc. part B. 1994; 6.
12. Perine J, Krepelka J. Quantum statistics of optical parametric processes with squeezed reservoirs. Optical Commun. 2015; 308: 274-281.
13. Anwar J, Zubairy MS. Phys Rev A.1992; 45: 1804.
14. Bashe B, Kassahun F. Quadretuare squeezing in the cavity mode driven by coherent light & interact with two-level atom. Int J Mole Theoretical Phys.2018; 10.