Magnetohydrodynamic (MHD) stability of wendelstein7-X reactor with resistive wall (RWMs)

Plasma stability is the biggest challenge facing the nuclear fusion industry. One of the best methods of stability study is magnetohydrodynamic (MHD) equations, which has two linear and nonlinear states. Usually linear stability analysis is used to describe the MHD state, which is obtained by linearizing nonlinear equations. The reactor under study is the W7-X reactor, which is an optimal example of a stellaratoric system.

The question raised in this research is how to create suitable conditions for the formation of plasma and heat transfer produced by the melting reaction. Many efforts have been made in this direction, but still the record holder for plasma state maintenance belongs to the international ITER project and around 1000. However, IPP researchers at the Max Planck Institute in Germany (maker of the W7-X reactor) predicted that by 2020 they would produce a pulse of 30 minutes.

The numerical method is used to investigate the stability of the reactor. In this paper, boundary conditions were expressed in terms of resistance wall. With the help of the mathematical Matlab software, magnetic field values ​​were obtained from experimental reports extracted from the Max Planck Institute for various values ​​of β. From the values ​​obtained, it was concluded that the appropriate field value is β = 5 according to the ideal MagnetoHydroDynamic state and the interval defined by the Max Planck Institute.

The term plasma is called ionizing gas, all or a significant portion of its atoms lost one or more electrons and turned into positive ions. The plasma used in nuclear reactors consists of two light elements that are generally hydrogen isotopes, such as deuterium and tritium. The advantages of this plasma include: inherent electrical conductivity and magnetic field, field production during motion, the effect of plasma diamagnetism that can produce internal magnetic field. The plasma mirror property of the plasma happens when moving from regions of higher density to lower density.

Production and maintenance of the plasma is very difficult. The first problem in this area is that it is not possible to supply hydrogen fuel as much as the sun on Earth. The next problem is the plasma’s behavior, when it is very much at a high temperature and pressure, it becomes extremely unstable and difficult to maintain. For this reason, plasma stability is of particular importance in the nuclear fusion industry [1,2].

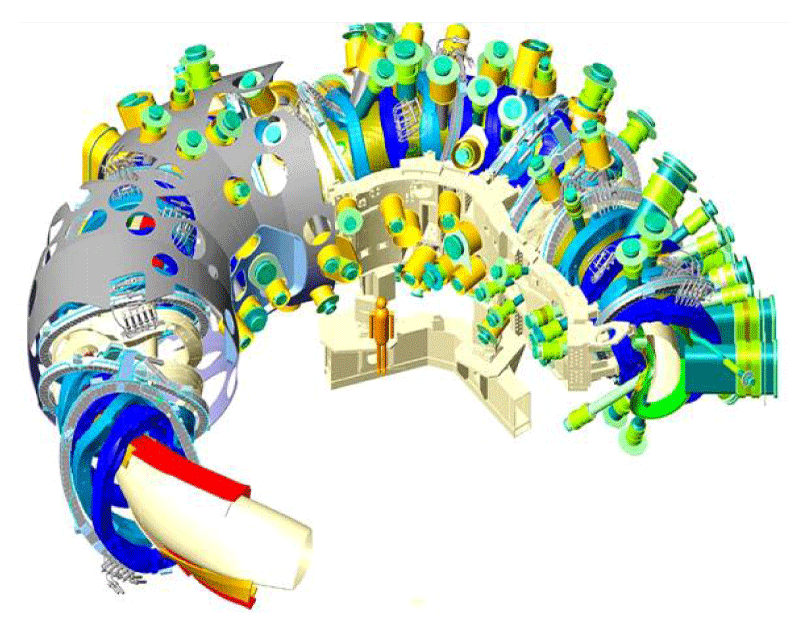
The design and construction of fusion reactors for long years of power use have been the goal of scientists throughout the world. The Max Planck Institute, which has been working on plasma physics for decades, unveiled the 2015 W7-X reactor. This is an advanced prototype reactor for the W7-AS, designed and used as the power plant. The enclosure of this reactor consists of 50 non-level rewinds and 20 flat rewinds. The rewinds create a magnetic field that encloses a hydrogen plasma with a temperature of more than 100 million degrees [3,4] (Figure 1).

The W7-X reactor consists of 5 sections, which include a plasma chamber, thermal insulation, ten wires in a stellarator and four flat wires, which are fitted with tubes for cooling the wires. It has a central support ring and an outer compartment where all these units are interconnected. An integrated plasma thermal and monitoring system that insulates the plasma. At the same time, the coil heating and cooling system cools through the use of liquid-cooled helium. The reactor plasma enclosure is a steel tube used to refine a hydrogen plasma at a temperature of 100 million degrees. The circle of the plasma-like ring has an outer radius of 12.8 meters and a height of 2.5 meters. The stainless steel chamber is completely aligned with the magnetic field and encloses the hot plasma. Linear magnetohydrodynamic equations for input values ​​such as flow rate, magnetic field, and flux of the plasma center, the variable values ​​at any moment including the magnetic field and instantaneous flux, the initial state variables include factors that can be changed by changing the stability margin It depends on the magnetic field of the vacuum chamber and the energy of the initial state.

Magnetohydrodynamic equations are: [5,6]

Maxwell’s Law at Low Frequencies:

$\nabla \text{x}B={\mu }_{0}j$ (1)

The adiabatic energy equation in liquids:

$\frac{d}{ dt}\left(\frac{p}{{\rho }^{\gamma }}\right)=0$ (2)

Ohm Law in Liquids:

$E+v\text{x}B=0$ (3)

Maxwell’s law:

$\frac{\partial B}{\partial t}=-\nabla \text{x}E$ (4)

The law of mass survival:

$\frac{\partial \rho }{\partial t}+\nabla ·\left(\rho v\right)=0$ (5)

The second law of Newton in liquids: ρ Magnetohydrodynamic stability rules dare needed to create and maintain some magnetic settings, eliminate energy shortages, and stabilize. The key to sustainability is to understand sustainability constraints through the use of a variety of plasma configurations and to create effective tools to address these constraints. So far, much research has been done in this regard. In the context of sustainability, the precise prediction of instabilities must first be done, which is possible with magnetohydrodynamic physics.

The second law of Newton in liquids:

$\rho \frac{dv}{dt}=-\nabla p+j\times B$ (6)

As stated in the introduction, stability in plasma is the biggest challenge for fusion reactors. Plasma stability is achieved by finding the points of equilibrium of each part. In many samples (in β less than 10), it can be treated with plasma as a liquid, whose stability analysis is investigated by magnetohydrodynamic method and has two linear and nonlinear states. Usually linear stability analysis is used to describe the magnetohydrodynamic state, which is obtained by linearizing nonlinear equations and methods. In order to maintain magnetohydrodynamic stability, various devices such as magnetic mirrors and radiation systems are used.

For example, in some enclosures, the FRC system (a device that encloses the plasma in the magnetic field lines and the center of which is the field lines passing through the entire Donut shape of the plasma) is used. Linear magnetohydrodynamic (MHD) equations for input values ​​such as flow intensity, magnetic field and flux of the plasma center are dependent. At each instant, the variable values including the magnetic field and instantaneous flux, and the initial state variables can be changed. The changes of the stability range, depends on the magnetic field of the vacuum chamber and the energy of the initial state [7,8].

β, is the ratio of plasma pressure to magnetic field.

$\langle \beta \rangle =5\%$

Stability of MHD is achieved at certain β values in a fusion reactor. The fusion power density is approximately {β2} in the constant or variable magnetic field $\left\{{\beta }_N^4\right\}$ as a constant Bootstrap diameter in the external plasma flow settings. Here ${\beta }_N=\beta /(\frac{I}{aB})$ in many cases the MHD stability indicates the initial beta limitation and thus the fusion strength density.

Helias (advanced helix stellaratoric) is a structure used by the Griffield Institute (IPP) for fusion systems. The equilibrium and stability of a helicoidally system in different values ​​of β (1-5)%, and considering the resistance conductor wall at the plasma boundary and the ideal magnetohydrodynamic (MHD) state by using Fourier expansion and MATLAB software, were calculated.

Then the magnitude of the magnetic field in the winding and the vacuum chamber is investigated. After calculating, the limits of β are obtained in the state of equilibrium and the intensity of the magnetic field. In this research, using mathematical software, magnetic field and current values ​​are determined in a crimped wire, and for different values ​​of β, and taking into account the principles of magnetohydrodynamic (MHD) stability. Then, the values ​​obtained for verification were compared to the values ​​of OP1.2a that were in the desired range. At the end, the range and the appropriate field and current values ​​were determined in β.

$\langle \beta \rangle =2\%$
$\langle \beta \rangle =3\%$
$\langle \beta \rangle =4\%$
$\langle \beta \rangle =5\%$ (7)

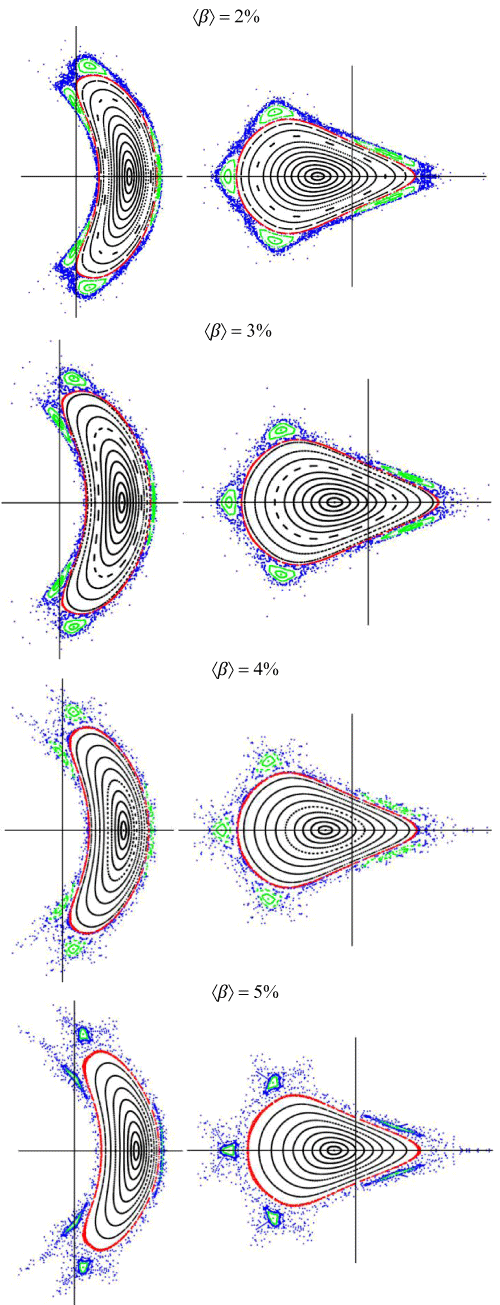
Magnetic field in different β values, black lines are red lines of the area under study and blue magnetic field lines are outside the area under study [9-11].

In the proposed Poincarés, it is evident that at values of β less than 4.2, the surface flux is not continuous according to figure 2, and this flux rupture and weak field at the edges cause turbulence and instability in the plasma structure. Comparison of the results of the magnetic field values obtained at β and the magnetic field of the vacuum chamber indicates that the Scheffranov transfer (radial flux transfer) is controlled and small due to the enclosing structure, but the rotational transfer decreases with increasing β. In stellar structures, then, what causes major instability is the rotational transfer of the plasma.

The black lines of the magnetic field are the red lines of the area under study and the blue lines of the magnetic field are outside the area under study.

Figure 2, magnetic field in different β values. (The black lines standing for magnetic field, red lines for magnetic field under investigation and blue lines are the magnetic field outside the area under investigation). In Poincare, it is evident that in β less than 4.2, the surface flux is not continuous in relation to figure 2. This fluctuation in flux and weakness of the field at the edges cause disturbance and instability in the structure of the plasma. The comparison of the results of the magnetic field values ​​obtained at β and the magnetic field of the vacuum chamber suggests that Shifanoy’s transmission (radial flux transfer) due to the constricted structure is controlled and small, but the rotary transfer decreases with increasing β. Therefore, in stellar structures, what causes major instability is the plasma spin transfer [9-11].

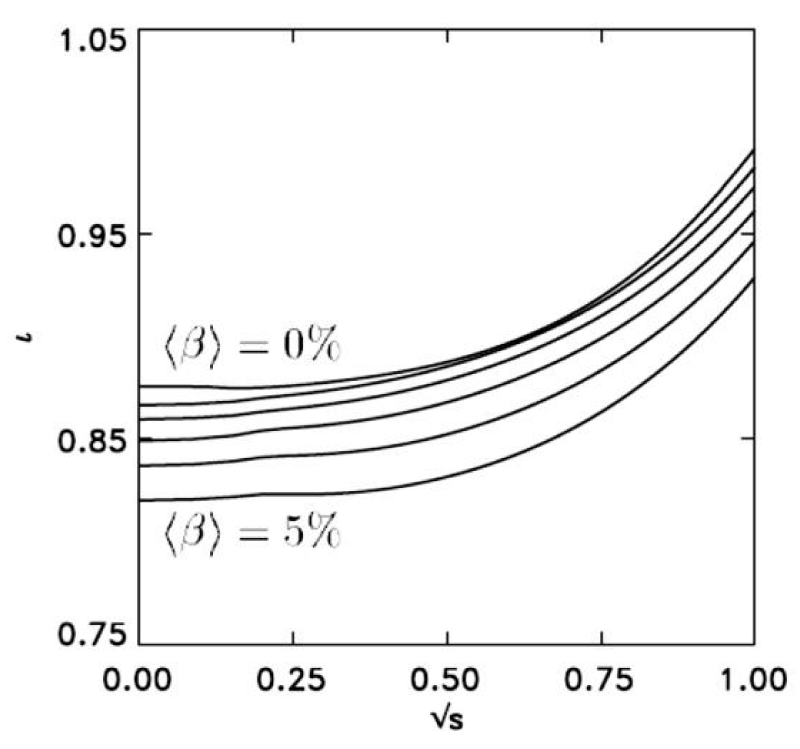
Figure 3 shows the profile changes l. When the rotary transfer increases, the plasma pressure also increases.

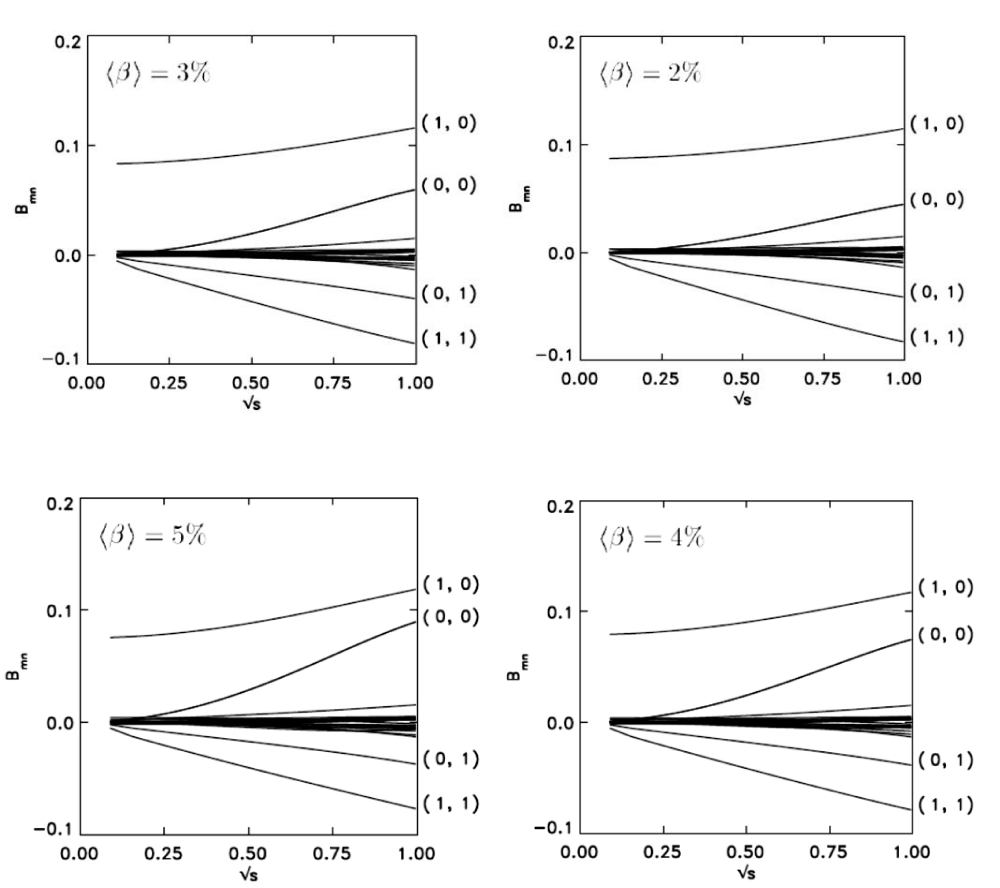
In Figure 4, the dependence of the function B_0.0 on the value of β is greater than the other points. It indicates that a strong magnetic field increases the pressure by increasing the amount of β. In small amounts of beta (β), it is possible to increase the amount of β by applying changes in the enclosing geometry and surface flux, for example, the application of an external magnetic field. The MagnetoHydroDynamic (MHD) stability properties indicate the β -balance equilibrium.

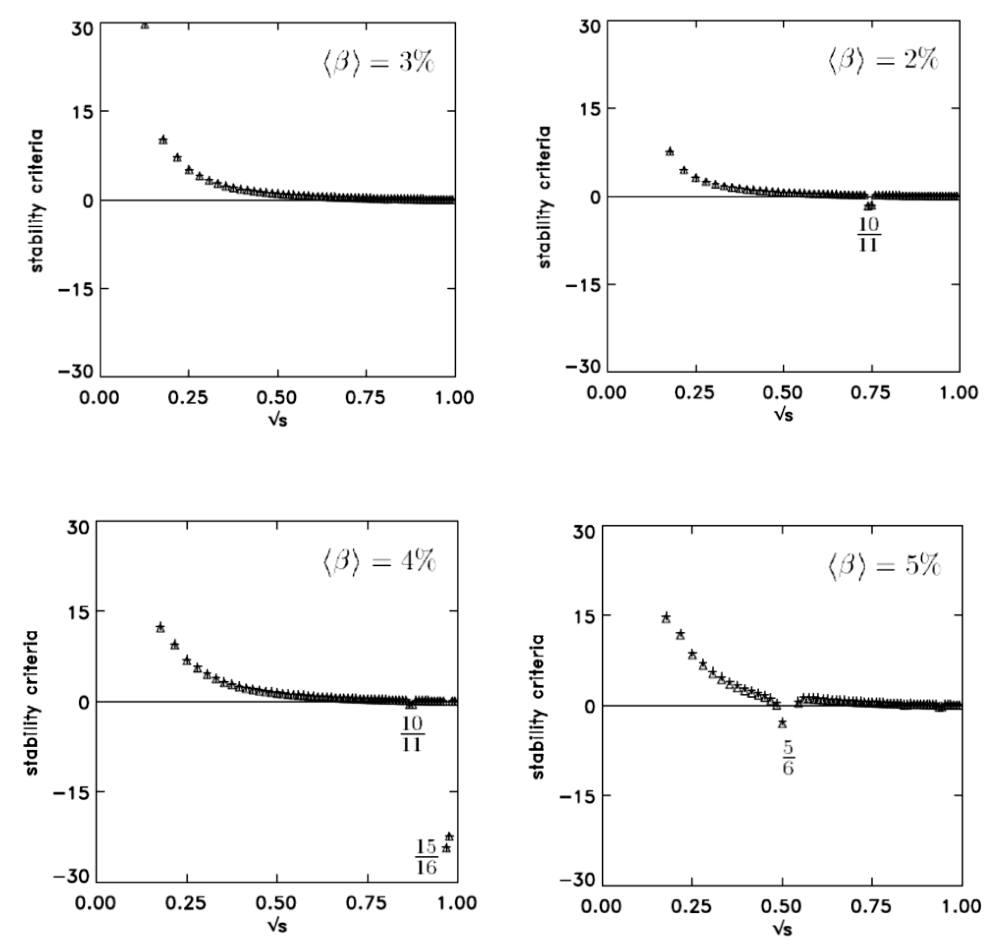
Figure 5 shows the critical stability points for different β values. For different magnetic fields and different values ​​of m = 0.1, ⋯ .23 poloidal and n = -24. ⋯ .0. ⋯ .24 for toroidal, Fourier coefficient, high resonance (like m/n = 15/16) around a surface flux is detected and the instability is solved at √ s = 0 ∙ 5 and at β = 5%, with a low resonance occurring at about 6.5 m/n.

The equilibrium equation in <β> = 4% has been investigated using CAS3D code in previous studies. The result of this study is a parameter that can be used in various fusion systems to test the stability of the reactor. For the different values ​​of Fourier 5 distribution, the range is considered. These parameters are used to compare the stability conditions of the W7-X reactor (64 points in radius, 115 Fourier distribution and N = 2).

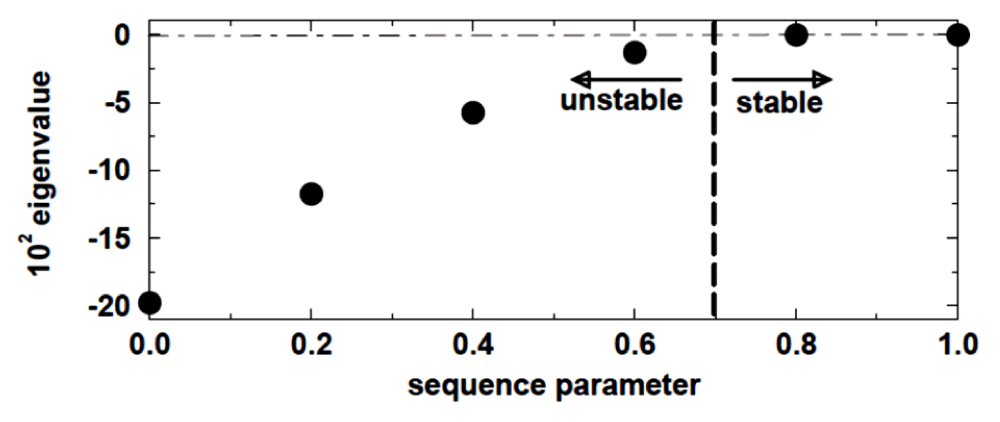
Figure 6 shows the results of the ideal magnetohydro-dynamic (MHD) mode at <β> = 4%.

Horizontal axis is the ratio of rotational transfer and superficial flux. In sequence parameters less than 0.7 instabilty occurs. Figure 6 shows the pressure distribution for the parameter of 0.6. This case occurs at m = 9 and n = -8. The density of the plasma is distributed on a scalar scale and is in axial direction.

With respect to the field values ​​and rotational displacements obtained in <β> = 5%, the plasma of the reactor is more balanced in this <β> beta value. Plasma edges have β > ≥ 2%, which affects the internal and external perturbations. To overcome these disturbances, a magnetic resistive wall has been used to amplify the magnetic field and increase the pressure and β coefficient. Five areas were used in limited walls to strengthen the field. In each region, based on the lines of the field, a spot was made and the poloidal and throidal values ​​were obtained to obtain a rotary transfer.

From the experimental reports (references), flow rates were extracted in different stresses and positions of the plasma and the field strength were obtained for each of these flows. It was observed that the ideal field values ​​are <β> = 5%, and in the lower values ​​of β there is a discrepancy in fluctuations and Shiffer and rotational transmission. Shifanov’s transmission values ​​were very small and insignificant due to the stator system and its spiral structure. However, a rotating transition was observed that, with increasing plasma pressure and an increase in β, the transfer value was reduced.

In the values ​​of <β> = 4%, the ideal state is a magnetohydrodynamic (MHD), which applies to all fusion reactors to some extent and is in good safety. In future studies, special attention can be paid to the unstable factors such as long wavelengths, confinement of plasma edges, and the energy of plasma particles and to prevent the development of instability. In addition, we can use other means of magnetohydrodynamic (MHD) in counteracting plasma instabilities such as parallel flows and neoclassical fractures. The heating and plasma control methods of this reactor are also a good topic for research. It is hoped that such reactors could be native and used extensively in the country.

In the present analysis, the magnetized hydrodynamic equilibrium and stability indicates the optimum stability range of the W7-X reactor for producing power and neutron for medical and research purposes. In future studies, special attention can be paid to the unstable factors such as long wavelengths, confinement of plasma edges, and the energy of plasma particles and to prevent the development of instability. In addition, we can use other means of magnetohydrodynamic in counteracting plasma instabilities such as parallel flows and neoclassical fractures. The heating and plasma control methods of this reactor are also a good topic for research. It is hoped that such reactors could be native and used extensively in the country.

According to the field values ​​and the rotational transfer obtained at <β> = 5%, the reactor plasma is more balanced in this beta value. Plasma edges have <β> 2% which is affected by small internal and external disturbances. To eliminate these disturbances, a magnetic resistance wall has been used to strengthen the magnetic field and increase the pressure and β factor. Five areas with limited walls were used to strengthen the field. In each region, points were plotted based on field lines, and polloidal and troidal values ​​were obtained to obtain rotational transitions. From the experimental reports, the values ​​of the current in different stresses and positions of the plasma were extracted and the field strength was obtained for each of these currents. It was observed that the most ideal field values ​​exist at 〈β〉= 5% and at lower β values ​​the discontinuity in the flux and transfer of Scheffranov and rotation is seen. Scheffranov transfer rates were very small and negligible due to the stellar system and its helical structure. However, a rotational transfer was observed, which was associated with an increase in plasma pressure and an increase in β, decreasing the transfer rate.

1. Krawczyk. Commissioning and first operation of the pulse-height analysis diagnostic on Wendelstein 7-X stellarator. EUROFUSION WPS1-CP 16. 2016; 15268.
2. Klinger T. Performance and properties of the first plasmas of Wendelstein 7-X. plasma physics. Control Fusion. 2017; 59: 014018.
3. Warmer F. From W7-X to a HELIAS fusion power plant: on engineering considerations for next-step stellarator devices. Fusion Engineering and Design. 2017; 9518-9517.
4. Weller. Sigonficance of MHD effects in stellarator confinement. Ms- 313705 final paper. 2016.
5. Han R,  Zhu P,  Banerjee D, Cheng S,  Yan X, et al. Low-n global ideal MHD instabilities in the CFETR baseline scenario. Plasma Phys Control Fusion. 2020; 62: 085016 6.
6. Ze-Yu, Li, et.al. Low-n global ideal MHD instabilities CFETR base line scenario. Nuclear Fusion. 2018; 58: 016018.
7. Wolf RC, et al. Major results from the first campaign of the Wendelstein 7-X Stellarator. Nuclear Fusion. 2017; 57: 102020.
8. Laqua HP. Wendelstein 7-X Team, Overview of W7-X ECRH Results in OPI-2a. 30th Joint Russian-Germany Meeting on ECRH and Gyrotrons.* Gyrotrons are the most advanced high-power sources of millimeter wavelength radiation. They have been used for many years in electron-cyclotron-wave (ECW) systems of many existing fusion installations. EPJ of Conference. 2018; 187: 01011.
9. Snipes JA. Physics requirement for the ITER plasma control system. Fusion engineering and design. 2010; 85: 461-465.
10. Merkel P. Linear MHD stability studies with the STARWALL code. Physics, Plasma. 2015; 1508: 04911v1.
11. Rachel McAdams, Non-linear Magnetohydrodynamic instabilities in Advanced Tokomak plasma, PhD Thesis, University o York, 2014