More Information
Submitted: June 19, 2023 | Approved: June 24, 2023 | Published: June 26, 2023
How to cite this article: Kebede G. A Study of Complete and Incomplete Reactions of 12C +169 Tm System at Energy Range ≈ 4.16 –7.5 MeV/Nucleon. Int J Phys Res Appl. 2023; 6: 121-127.
DOI: 10.29328/journal.ijpra.1001061
Copyright License: © 2023 Kebede G. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Keywords: Alpha emitted; CF reaction; Excitation functions; Heavy-ion fusion; ICF reaction; Non-alpha emitted
Acronyms: HI: Heavy Ion; CF: Complete Fusion; ICF: Incomplete Fusion; CN: Compound Nucleus; EFs: Excitation Functions; ERs: Evaporation Residuals
A Study of Complete and Incomplete Reactions of 12C + 169Tm System at Energy Range ≈ 4.16 –7.5 MeV/Nucleon
Getahun Kebede*
Department of Physics, Mizan Tepi University, Ethiopia
*Address for Correspondence: Getahun Kebede, Department of Physics, Mizan Tepi University, Ethiopia, Email: gkebede120@gmail.com; getahunkebede@mtu.edu.et
Most nuclear reactions are studied by inducing a collision between two nuclei (nucleon-nucleon reaction) where one of the reacting nuclei is at rest (the target nucleus) while the other nucleus (the projectile nucleus) is in motion. Projectiles heavier than α-particle (i.e. A≥4) are commonly regarded as heavy ions and become used for bombarding the target nuclei.
It is now generally recognized that several reaction mechanisms are operative in heavy ion-induced reactions below 10 MeV/nucleon. In fact, the cluster structure has been suggested as one of the factors leading to forward peaked α-particles in ICF reactions. While CF has been defined as the capture of the total charge or mass of the incident projectile by the target nucleus.
However, the first evidence of ICF reactions was presented by Kauffmann and Wolfgang [1], by studying the 12C +102Rh system at an energy range of 7-10 MeV/nucleon, where strongly forward peaked angular distributions of light-nuclear-particles were observed. Britt and Quinton [2], found similar observations in the 16O+209Bi reactions at energies range 7-10 MeV/nucleon. In these measurements, a significantly large yield of direct α-particles of mean energy roughly corresponding to the projectile velocity at the forward cone has been observed [3-7].
Meanwhile, the IFC system (reduced CN) forms with relatively less mass/charge and excitation energy (due to partial fusion of projectile), but at high angular-momenta (imparted due to noncentral interactions) as compared to the CN formed via CF.
In the past various studies were done on the mechanism of CF and ICF reactions. Recently Amanuel, et al. [8] studied the role of the breakup process in the fusion of the 12C + 52Cr system at several beam energies from ≈ 4-7 MeV/nucleon. It was found that from non-α-emitting channels the experimentally measured excitation functions were, in general, found to be in good agreement with the PACE4 predicted. Unlikely, for α-emitting channels the measured EFs were higher than PACE4 predicted which is attributable to ICF reactions.
A number of studies in the past were confined to beam energies greater than 10 MeV/nucleon and the reaction mechanism has been reasonably explained by the available models. Dynamical models, such as the Sum rule model [9], break-up fusion (BUF) model [10], and promptly emitted particle model [11] have been proposed to explain the mechanism of ICF reactions. However, no theoretical model is available so far fully to explain the gross features of experimental data available below E/A = 10 MeV/nucleon. Despite a number of attempts in the past none of the available models are able to reproduce the experimental data obtained at energies as low as 48 Mev/nucleon. As a result, no comprehensive evaluation of the ICF process has been done, necessitating further research, particularly at relatively low bombardment energies of 10 MeV/nucleon, where a clear systematic study and compiled data are available for only a few projectile target systems.
In this work the experimentally measured (EXFOR data) EFs for reactions 169Tm(12C, 4n)177Re, 169Tm(12C, 5n)176Re, 169Tm(12C, αn) 176Ta, 169Tm(12C, α2n)175Ta, 169Tm(12C, α3n)174Ta, 169Tm(12C, α4n)173Ta and 169Tm(12C, 2α2n)171Lu in the incident energy range 50 - 90 MeV were compared with theoretical predictions based on PACE4 codes. The PACE4 theoretical model was applied with 100,000 cascades to predict the measured excitation function.
Computer code and formulation
There are various computer codes such as PACE4, CASCADE, and COMPLETE CODE (modified of ALIC- 91) that are available to perform such statistical model calculations. The PACE4 [12] code was chosen to be used in the present work since it is easily available and proved to be one of the most reliable and promising theoretical models for compound nuclear reactions. This section also includes an analysis of the Hauser-Feshbach formulation using the computer code PACE4.
The code uses the BASS model for CF cross-section computation and employs the Hauser-Feshbach formalism to determine the decay of the sequence of an excited nucleus. In this statistical code for neutrons, protons, and α-particles the default optical model parameters are used. In addition, a code has been modified to take into account the excitation energy dependence of the level density parameter using the prescription Kataria, et al. [13]. It should be pointed out that the ICF and PE-emission are not taken into consideration in this code. The process of de-excitation of the excited nuclei was calculated using code PACE4 which follows the correct procedure for angular momentum coupling at each stage of de-excitation.
Therefore, PACE 4 predictions were found to be in good agreement for complete fusion channels for the present projectile-target system and are appropriate for heavy ion-induced reactions (as seen from different papers) excitation functions in this work are calculated by this code. The angular momentum projections are calculated at each stage of de-excitation, which enables the de-excitation of the angular distribution of the emitted particles. The complete fusion (CF) cross-sections of the system are calculated using the Bass formula. In this code, the level density parameter a is given by: a=A/K Where A is the mass number of the compound nucleus and K is a free parameter.
For any projectile energies that are given to bombarding the target, the partial cross-section for CN formation at angular momentum (l) is given by:
(1)
As a result, the cross-section is calculated using Morgenstern, et al. [14] to compare measured EFs with theoretical predictions obtained from PACE4 for possible residues populated in the reaction.
(2)
In order to extract more information regarding how ICF contributes to total fusion reaction cross section is given by:
(3)
From this cross-section, the total ICF cross-section can be found using an expression of
(4)
The enhancement from the theoretical predictions points towards the presence of the ICF process in the formation of all ERs, the contribution of ICF in the formation of all α-emitting channels has been calculated as
(5)
The contribution of ICF in the formation of all non -α-emitting channels has not been observed due to no α cluster being populated by the breakup process.
and it is true for each individual ERs.
In this work, the excitation functions for seven residues produced in the 12C +169Tm system were studied. The experimentally measured excitation functions were compared with the theoretical predictions obtained from the code PACE4. The experimental cross-section and energy are obtained from the IAEA data source (EXFOR) Library [15].
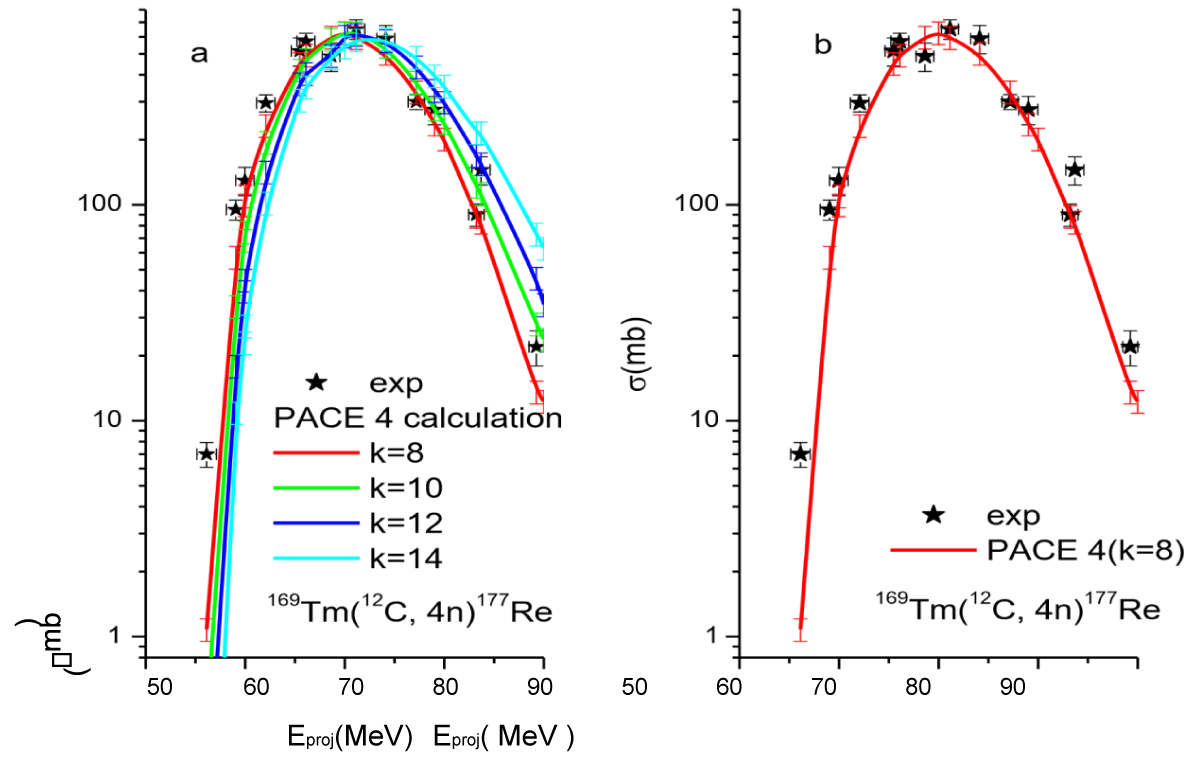
In order to show the effect of variation of K on calculated EFs, different values of K = 8, 10, 12, and 14 have been tested, and are shown in Figure 3.1 (a). Therefore in this work, a value of K = 8 is found to give a satisfactory reproduction of experimental data for CF channels within the experimental uncertainties and has been chosen confidentially for other -emitting channels.
Figure 3.1: Experimentally Excitation function for the 169Tm(12C, 4n) 177Re reaction used for studying the effect of the value of k on theoretically calculated results expected to be populated by CF compared with their theoretical prediction (PACE4) a) at different k value and b) at k = 8 that has been best fitted within the energy range ≈ 4.16–7.5 MeV/nucleon.
Evaporation residues populated through non-α-emitting (12C, xn) channels
A. (12C, 4n) channel
For the representative (12C, 4n) channel values of the level density parameter K (K = 8, 10, 12, and 14) were varied to fit the experimental data, and the results are displayed in Figure 3.1. When the 12C projectile entirely merged with the 169Tm target, the excited compound nucleus 181Re* was formed, resulting in the production of the 177Re residue through the emission of four neutrons from excited CN. In reaction equation form, it is written as:
12C + 169Tm → [181Re]* → 177Re + 4n
As can see from Figure 3.1 the theoretically calculated excitation function corresponding to the level density parameter K = 8 in general satisfactorily reproduced the experimentally measured EFs for residue 177Re produced in the CF of 12C projectile with 169Tm target. In the present calculation, a value of K = 8 will be used for all other residues populated in the 12C + 169Tm system. Further, it may be mentioned that the general trends and shape of the measured EFs for the CF residues populated 4n channels are satisfactorily reproduced by PACE4 calculations with uncertainties for the entire energy region as shown in Figure 3.1.
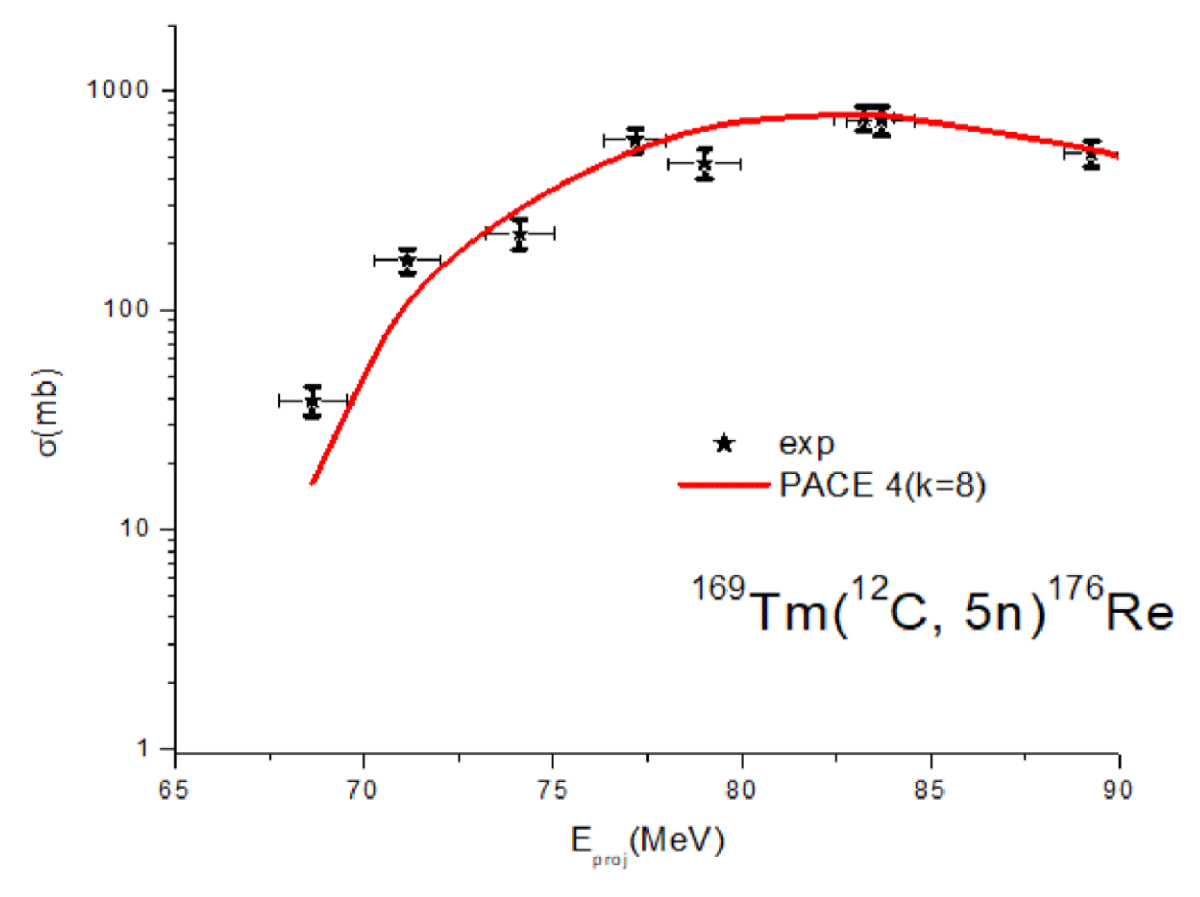
B. (12C, 5n) channel
The 176Re residue was produced when the 12C projectile completely fused with the 169Tm target leading to the formation of excited compound nucleus 181Re*. The excited CN, 181Re*, decays through the emission of five neutrons that leads to the formation of isotope 176Re. In reaction equation form, it is written as:
12C + 169Tm → [181Re]* → 176Re + 5n
The experimentally measured EFs along with theoretical predictions obtained using the PACE4 code residues populated via non α-emitting channels (12C, 5n) are shown in Figure 3.2. The theoretically calculated excitation function corresponding to the level density parameter K=8 in general satisfactorily reproduced the experimentally measured EFs for residue 176Re produced via the CF of 12C projectile with 169Tm target.
Figure 3.2: Experimentally Excitation function for the 169Tm(12C, 5n) 176Re reaction populated by CF compared with their theoretical prediction (PACE4) at k = 8 within the energy range ≈ 4.16 – 7.5 MeV/nucleon.
Evaporation residues populated through α - emitting (12C, αxn) channels
In the interaction of the 12C projectile with the 169T m target at energies of ≈ 56.12 -90 MeV, a total of five ERs were found to get populated through the α emitting channels in this work. The EFs of these ERs (Figures 3.3 - 3.7) show an appreciable enhancement over the theoretical values predicted by the statistical model code, PACE4.
As can be seen from Figures 3.3 - 3.7 displayed the experimentally measured EFs along with theoretical prediction obtained from PACE4 for 177−xTa(x=1, 2, 3, 4) and 171Lu were formed by the reactions of (12C, αxn) and (12C, 2α2n) channels respectively. Thus, the ERs populated through α emitting channels there is the prospect of ICF and therefore the contributions were arising from the CF as well as enhancing the credit and the effect of ICF processes.
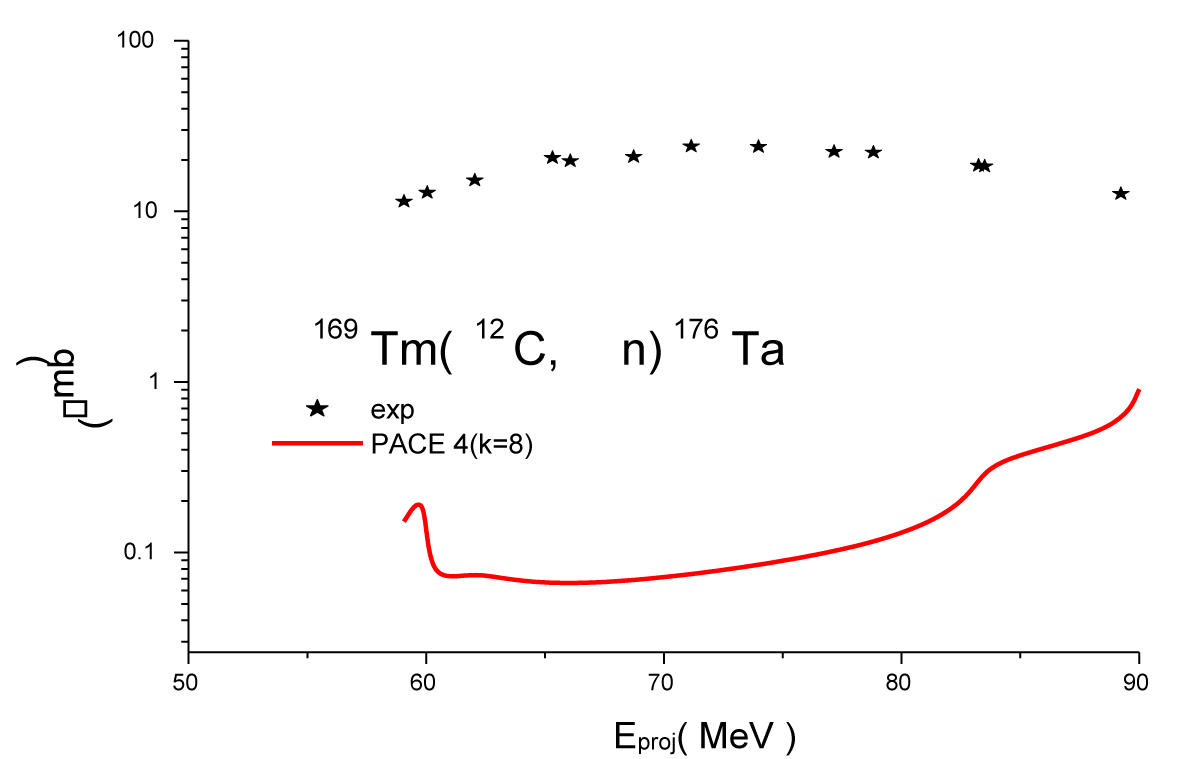
Figure 3.3: Experimentally Excitation function for the 169Tm(C,αn)176Ta reaction compared with their theoretical prediction (PACE4). C(8Be + α) +169Tm → α + [177Ta]* → 155Ta + α +2n.
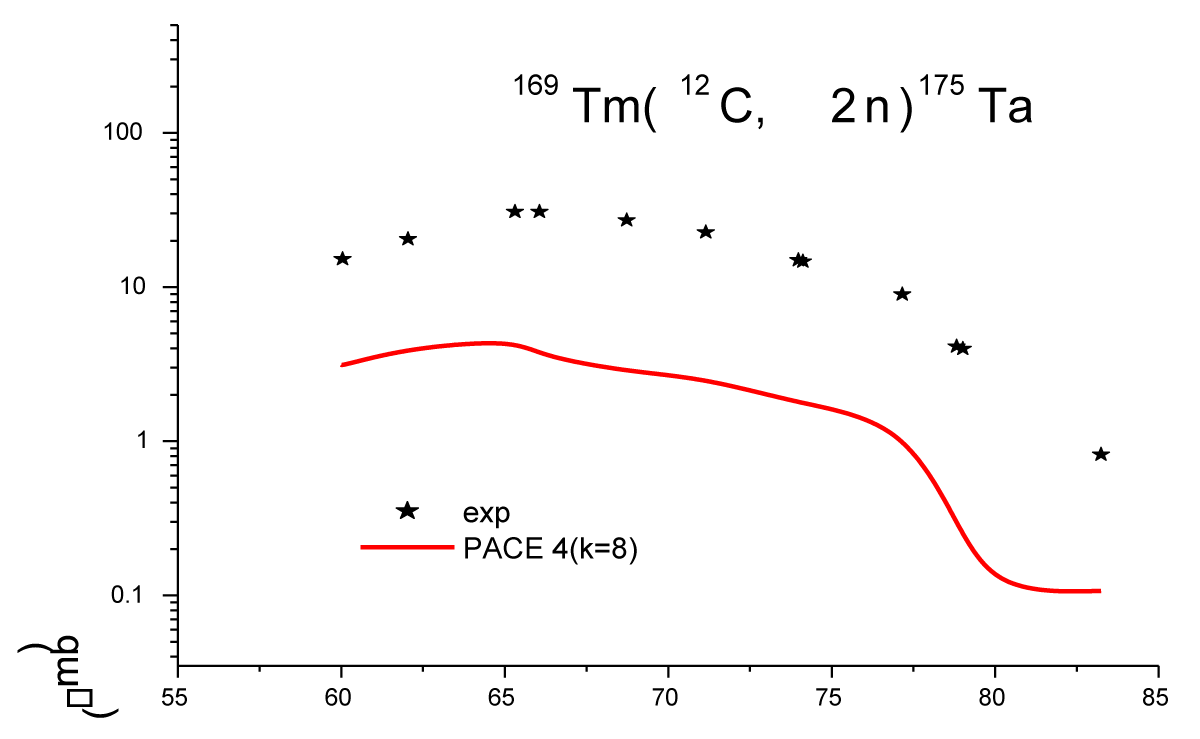
Figure 3.4: Experimentally Excitation function for the 169Tm(12C, α2n)175Ta reaction compared with their theoretical prediction (PACE4).
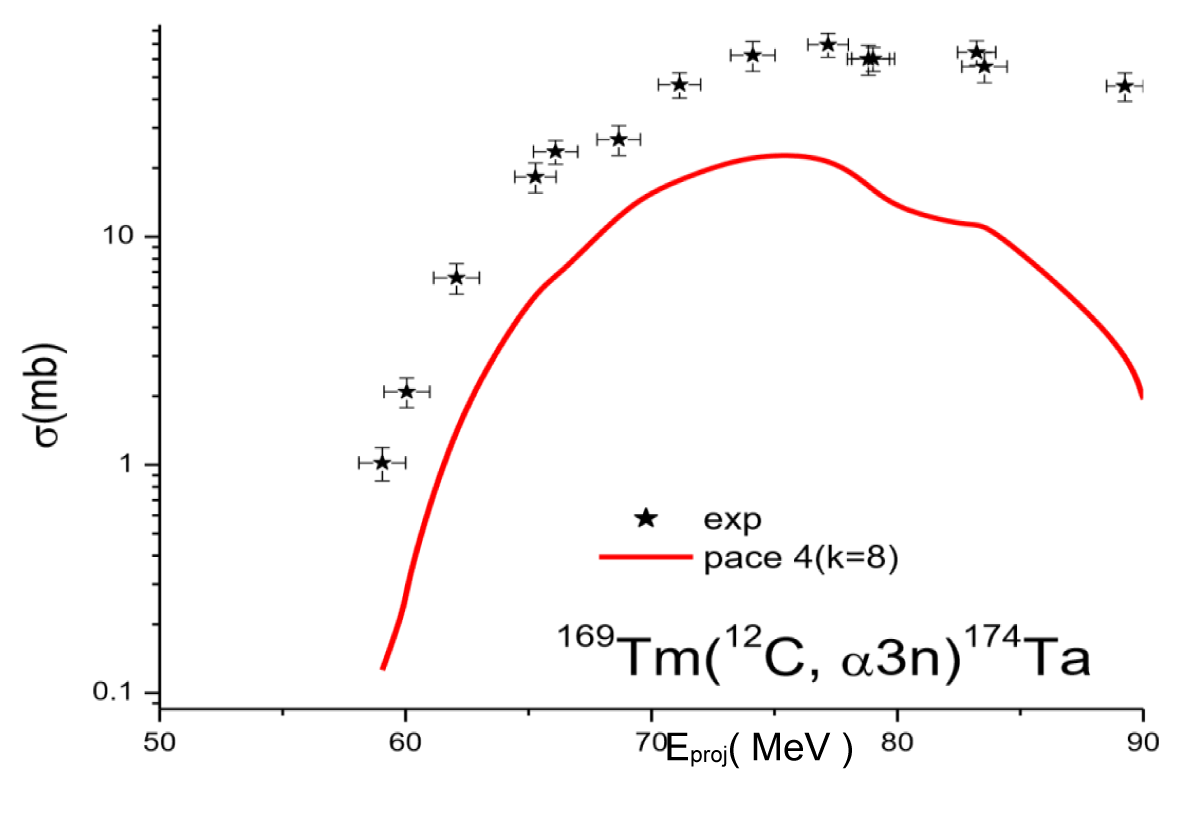
Figure 3.5: Experimentally Excitation function for the 169Tm(12C, α3n)174Ta reaction compared with their theoretical prediction (PACE4).
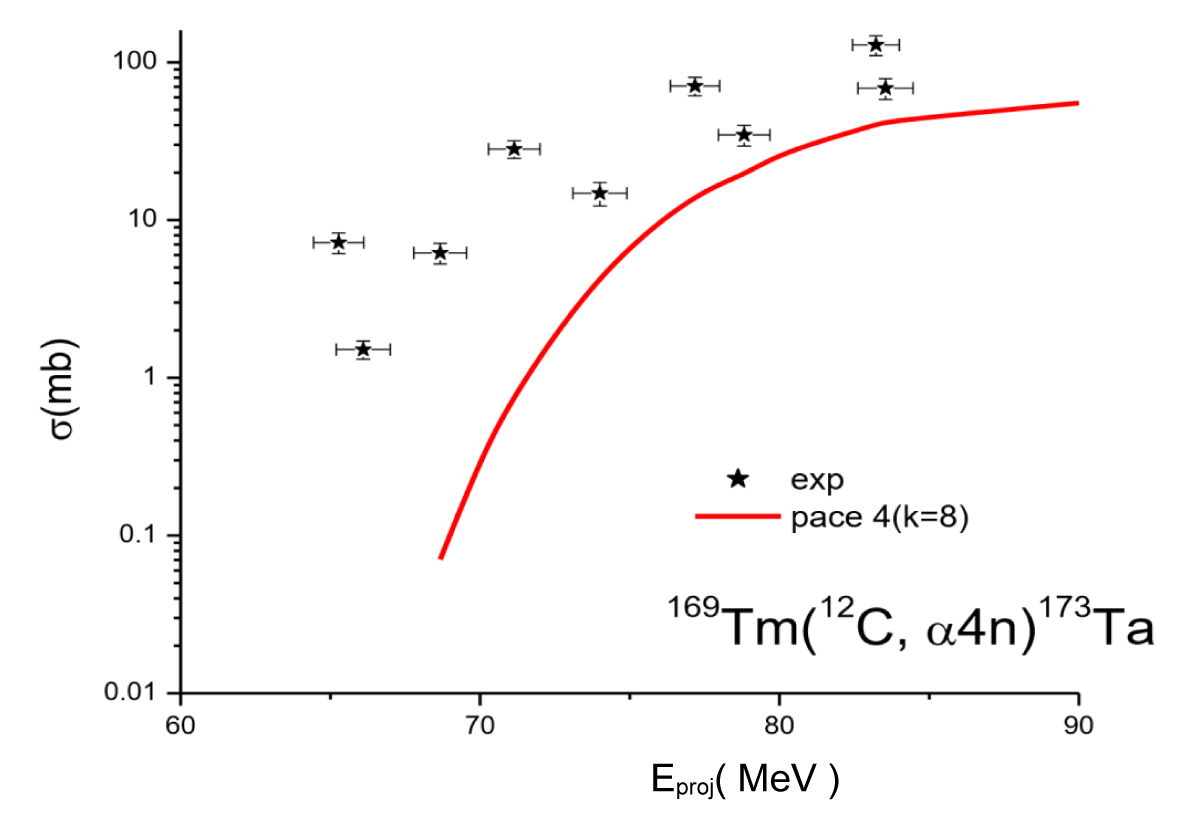
Figure 3.6: Experimentally Excitation function for the 169Tm(12C, α4n)173Ta reaction compared with their theoretical prediction (PACE4).
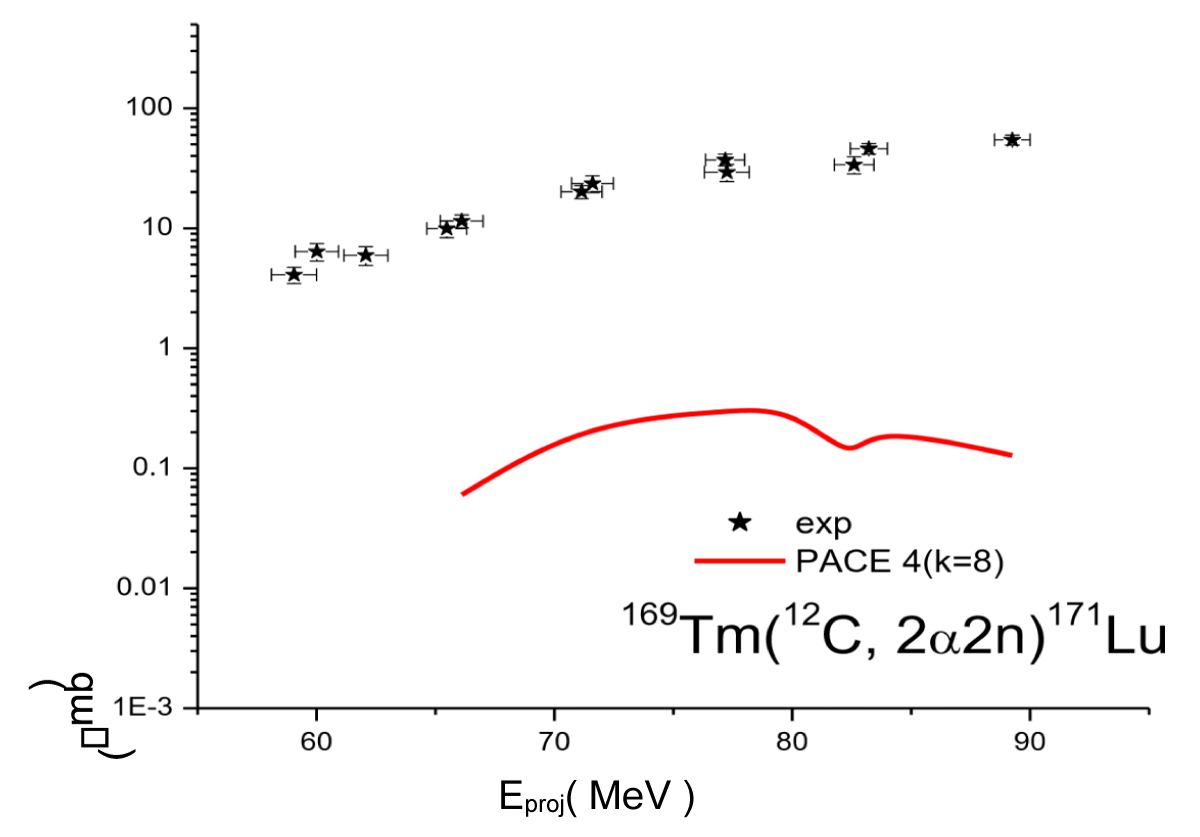
Figure 3.7: Experimentally Excitation function for the 169Tm(12C, 2α2n)171Lu reaction compared with their theoretical prediction (PACE4).
Therefore, since the code PACE4 does not take ICF reactions into account, the mismatch between theoretically obtained data and experimental data and any enhancement over the PACE4 values is attributed to the contribution arising from the ICF process. It is also observed that the degree of ICF contributions, in the formation of ERs populated through α -emitting channels were varying from residue to residue and take the largest contribution of the reaction of all α emitting channels which are presented in this section.
A. (12C, αn) channel
The 176Ta residue was produced when the 12C projectile completely fused with the 169Tm target leading to the formation of excited compound nucleus 181Re* and 12C incompletely fused with 169Tm led to the formation of composite system 177Ta. This residue may be formed via CF and/or ICF in the interaction of 12C with 169Tm following two processes. i). In the case of CF, the composite system 181Re*, decay through the emission of one cluster and one neutron that leads to the formation of isotope 176Ta. ii) The same residue is formed by ICF of 12C breaks into α+8Be, and 8Be fuses with the target by leaving α cluster particle as a spectator to form an incompletely fused composite system [177Ta]*, which may then decay via emission of one neutron (n). In reaction equation form, it is written as:
I. Complete fusion (CF) of 12C:
12C + 169Tm → [181Re] → 176Ta +αn
Where α is acting as a participant, not as a spectator.
II. Incomplete fusion (ICF) of 12C
12C (8Be +α) +169Tm α + [177Ta] → 176Ta + α + n
(α as a spectator will not participate in the reaction).
As can be seen from Figure 3.3, the experimentally measured EFs are higher as compared to the theoretical predictions in the energy range of 59.06 - 90 MeV level. Since the PACE4 code does not take ICF into account, therefore the enhancement in the experimentally measured cross sections is attributed to the contribution of ICF of 12C with 169Tm target.
B. (12C, α2n) channel
The 175Ta residue was produced when the 12C projectile completely fused with the 169Tm target leading to the formation of excited compound nucleus 181Re* and 12C incompletely fused with 169Tm led to the formation of composite system 177Ta. This residue may be formed via CF and/or ICF in the interaction of 12C with 169Tm following two processes. i) In the case of CF, the composite system 181Re*, decay through the emission of one α cluster and two neutrons that leads to the formation of isotope 175Ta. ii) The same residue is formed by ICF of 12C breaks into α+8Be, and 8Be fuses with the target while leaving α particle as a spectator to form an incompletely fused composite system [177Ta]*, which may then decay via two neutrons (2n).
In reaction equation form, it is written as:
I. Complete fusion(CF) of 12C:
12C + 169Tm → [181Re] → 175Ta +α2n
(α as a participant in the reaction, not as a spectator)
II. Incomplete fusion(ICF) of 12C:
As can be seen from Figure 3.4, the experimentally measured EFs are higher as compared to the theoretical predictions. As such, it may again be inferred that the major contribution of the enhancement for the production of these residues comes from ICF processes, which are not considered in these calculations in the interaction of 12C with the 169Tm target.
C. (12C, α3n) channel
The 174Ta residue was produced when the 12C projectile completely fused with the 169Tm target leading to the formation of excited compound nucleus 181Re* and 12C incompletely fused with 169Tm led to the formation of composite system 177Ta. This residue may be formed via CF and/or ICF in the interaction of 12C with 169Tm following two processes. i) In the case of CF, the composite system 181Re*, decay through the emission of one α cluster and three neutrons that leads to the formation of isotope 174Ta. ii) The same residue is formed by ICF of 12C breaks into α+8Be, and 8Be fuses with the target while leaving α cluster as a spectator to form an incompletely fused composite system [177Ta]*, which may then decay via two neutrons (3n).
In reaction equation form, it is written as:
I. Complete fusion (CF) of 12C:
12C + 169Tm → [181Re] → 174Ta + 3n
(α as a participant, not as a spectator).
II. Incomplete fusion(ICF) of 12C:
12C (8Be + α) +169Tm → α + [177Ta] → 174Ta + α + 3n
(α as a spectator not a participant in the reaction).
The experimentally measured cross-section is relatively higher than the theoretical predictions as shown in Figure 3.5. Since the code PACE4 doesn’t take ICF into account, therefore the enhancement in the experimentally measured cross-sections is attributable to the contributions of ICF of 12C with 169Tm target.
D. (12C, α4n) channel
The 173Ta residue was produced when the 12C projectile completely fused with the 169Tm target leading to the formation of excited compound nucleus 181Re* and 12C incompletely fused with 169Tm led to the formation of composite system 177Ta. This residue may be formed via CF and/or ICF in the interaction of 12C with 169Tm following two processes. i) In the case of CF, the composite system 181Re*, decay through the emission of one α cluster and four neutrons that leads to the formation of isotope 173Ta. ii) The same residue is formed by ICF of 12C breaks into α+8Be, and 8Be fuses with the target while leaving α cluster as a spectator to form an incompletely fused composite system [177Ta]*, which may then decay via four neutrons (4n).
In reaction equation form, it is written as:
I. Complete fusion(CF) of 12C
12C + 169Tm → [181Re] → 173Ta + α4n
Where α is acting as a participant, not a spectator.
II. Incomplete fusion(ICF) of 12C
12C(8Be + α) +169Tm → α + [177Ta]* → 173Ta + α + 4n α as a spectator which is not participate on the reaction( act as observer).
The experimentally measured cross-section exhibits a significant enhancement compared to the theoretical predictions as can be seen from Figure 3.6. As such, it may again be inferred that the major contribution of this enhancement comes from ICF processes, which are not considered in these calculations.
E. (12C, 22n) channel
The 171Lu residue was produced when the 12C projectile completely fused with the 169Tm target leading to the formation of excited compound nucleus 181Re* and 12C incompletely fused with 169Tm led to the formation of composite system 173Lu. This residue may be formed via CF and/or ICF in the interaction of 12C with 169Tm following two processes. i) In the case of CF, the composite system 181Re*, decay through the emission of one 2α cluster and two neutrons that leads to the formation of isotope 171Lu. ii) The same residue is formed by ICF of 12C breaks in to 8Be(α + α)+ α and α nucleus fuses with the target while leaving 8Be as spectator to form an incompletely fused composite system [173Lu]*, which may then decay via two neutrons (2n).
In reaction equation form, it is written as I.
I. Complete fusion (CF) of 12C:
12C + 169Tm → [181Re] → 171Lu + 2α2n
(2α is as a participant in the reaction system, not as a spectator).
II. Incomplete fusion (ICF) of 12C:
12C(α + 8Be(α +α)) + 169Tm → 2α + [173Lu] → 171Lu + 2α + 2n (2 as a spectator, not a participant in the reaction).
In the case of reaction169Tm (12C, 2α2n) 171Lu, as can be seen from Figure 3.7 the experimentally measured EF exceeds the theoretical EF, which again indicates that ICF plays an important role. Since theoretical calculations of PACE4 do not take into account the ICF, it may be inferred that a significant part of these reactions involving 2α -emission channels go through ICF largely, at these energies.
Further, it is obvious that α-emitting channels have contributions coming from ICF reactions.
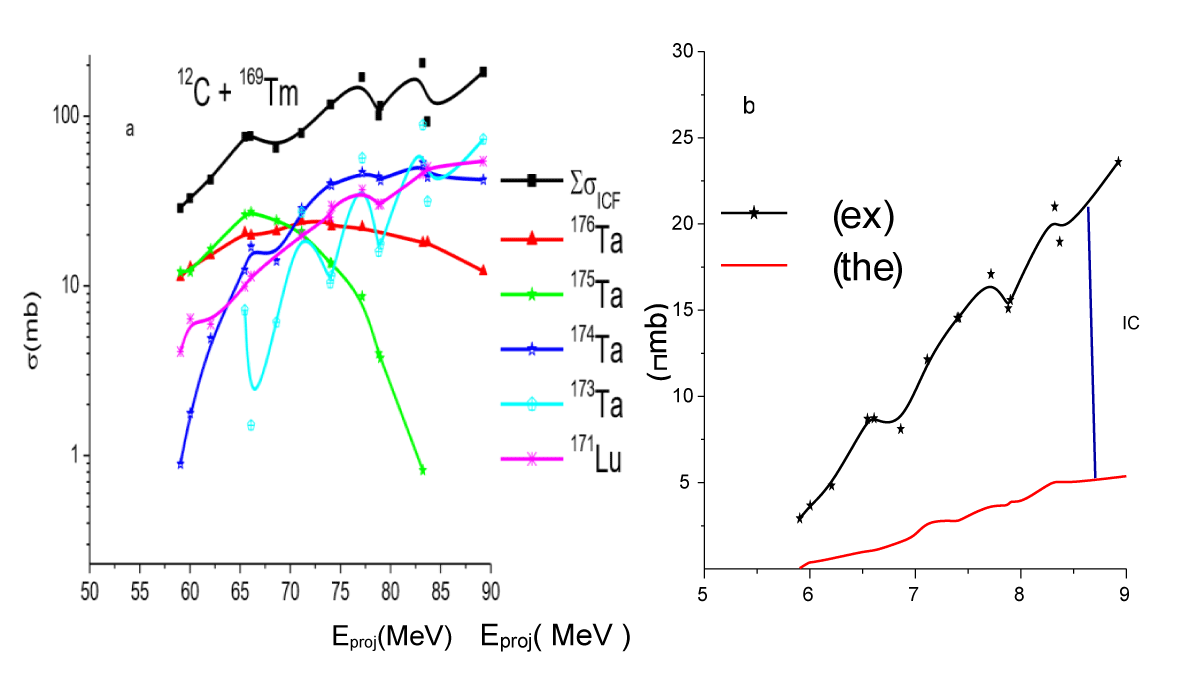
Therefore to provide the quantitative value of the ICF reaction cross section for the individual α-emitting channel we used Morgenstern formulation which also has been calculated using, at each point of energy. Figure 3.8(a) displayed the deduced individual ICF cross-section of the α-emitting channel along with their sum.
Figure 3.8: a): Deduced ICF contribution for individual residues along with the total sum of ICF cross-sections, for 12C + 169Tm reaction system. And b) the Sum of experimentally measured EFs of channels are compared with that t predicted by statistical model code PACE 4. (b): Displayed the sum of experimentally measured cross-section, along with the sum of PACE4 cross-section . As can be seen from this figure, there is a clear gap between these two values which is attributable to the contribution coming from ICF reactions.
As it can be seen from this figure the sum of the deduced ICF cross-section , in general increases with an increase in projectile energy.
Figure3.8 (b) displayed the sum of experimentally measured cross-section , along with the sum of PACE4 cross-section . As can be seen from this figure, there is a clear gap between these two values which is attributable to the contribution coming from ICF reactions. Further from this figure, the increasing separation between and indicates that when projectile energy is increased the contribution of the ICF also relatively increased.
In this work, the excitation function of 176, 177Re, 173,174,175,176Ta, and 171Lu evaporation residues produced via CF and/or ICF reactions in the interaction of 12C projectile with 169Tm target at energies ≈ 4.16 - 7.5 MeV/nucleon were studied. The experimentally measured EFs were compared with theoretical calculations done using the PACE4 code. For non-α emitting channels the experimentally measured production cross-sections were found to be in good agreement with theoretical. In such reactions a case, it expects the projectile to be completely fused with the target, which is a mechanism that can be effectively described by PACE4. However, for α emitting channel the theoretical predictions did not reproduce the experimental measured EFs. The observed enhancement may be attributed to the ICF processes from the break-up of the 12C projectile. 12C projectile breaks into 8Be and an alpha particle, and the 8Be fragment fuses with 169Tm, forming the incompletely composite nucleus, followed by the emission of neutrons and α-particle. The present analysis showed that in heavy-ion induced reaction mechanisms study, the contribution from ICF is an important component of fusion reactions in particular at higher energy points. Furthermore, the present study showed ICF cross-section in general increases with an increase in projectile energy. So it may be possible to conclude that complete and incomplete fusion reactions play important roles in heavy ion-induced reaction mechanism studies.
- Kauffmann R, Wolfgang R. Single-Nucleon Transfer Reactions of F19, O16, N14, and C12 Phys Rev. 1961; 121: 206.
- Britt HC, Quinton AR. Alpha Particles and Protons Emitted in the Bombardment of Au197 and Bi209 by C12, N14, and O16 Projectiles. Phys. Rev. 1961; 124: 877.
- M. Cavinato. Study of the reactions occurring in the fusion of 12C and 16O with heavy nuclei at incident energies below 10 MeV/nucleon. Phys Rev C. 1995; 52: 2577.
- P. Vergani. Complete and incomplete fusion and emission of preequilibrium nucleons in the interaction of 12C with 197 Au below 10 MeV/nucleon. Phys Rev C. 1993; 48: 1815.
- Abhishek Y, Vijay RS, Pushpendra PS, Kumar R, Singh DP, Unnati MK. Effect of a-Q value on incomplete fusion. Phys Rev C. 2012; 85: 034614; ibid 86: 014603.
- P. P. Singh. Influence of incomplete fusion on complete fusion: Observation of a large incomplete fusion fraction at E ≈ 5-7 MeV/nucleon. Phys Rev C. 2008; 77: 014607.
- Sharma MK, Singh BP, Gupta S, Musthafa MM, Bhardwaj HD, Prasad R, Sinha AK. Complete and Incomplete Fusion: Measurement and Analysis of Excitation Functions in 12C+128 Te System at Energies near and above the Coulomb Barrier. Journal of the Physical Society of Japan. 2003; 72: 1917-1925.
- Amanuel FK, Zelalem B, Chaubey A. K, Avinash AIA. Role of break-up processes in the fusion of the 12C + 52Cr system. Phy Rev C. 2011; 84: 024614.
- Lilly J. Nuclear Physics Principles and Applications 2001.
- Udagawa T,Tamura T. Breakup-Fusion Description of Massive Transfer Reactions with Emission of Fast Light Particles. Phys Rev Lett. 1980; 45:1311.
- Bondrofetal JP. Nucl Phys A. 1980; 333: 285.
- Tarasov OB, Bazin D. Development of the program LISE: application to fusion–evaporation. NIM B. 2003; 204: 174-178.
- Kataria SK, Ramamurthy VS, Kapoor SS. Semiempirical nuclear level density formula with shell effects. Phys Rev C. 1978; 18: 549.
- Morgenstern H, Bohen W, Galster W, Grabisch K, Kyanowski A. Influence of the Mass Asymmetry on the Onset of Incomplete and the Limit to Complete Fusion. Phys Rev Lett 1984; 52: 1104.
- https://www-nds.iaea.org