Estimating the Minimum Possible Deceleration of Cosmic Expansion Post-inflation

The inflationary epoch, occurring shortly after the Big Bang, initiated an extraordinarily rapid exponential expansion of the universe. Following this period, the rate of cosmic expansion decelerated for approximately 9.8 billion years, until observations indicated a transition to an accelerated expansion of space-time. This paper aims to estimate the minimum possible deceleration of cosmic expansion during the post-inflationary epoch, addressing an unresolved aspect of cosmological studies. The observable universe is modeled as a spherical region defined by the particle horizon in the FLRW metric. The model operates on the principle that the speed of light cannot exceed the speed of space-time expansion, given that photons are bound by space-time constraints. This paper hypothesizes that at the end of the 9.8 billion years of deceleration, the expansion speed was at its lowest, nearly equating to the speed of light. Subsequently, this speed has increased, correlating with the current accelerated expansion. Through a graphical representation assuming a uniform rate of change in expansion speed (for minimum possible values), we apply concepts of onedimensional motion to derive our estimates. This novel approach provides a foundational calculation of the minimum deceleration, significantly contributing to the understanding of the dynamics of cosmic expansion and offering a basis for future research and observational refinement.

The inflationary epoch, a cornerstone of modern cosmological theory, marks the period immediately following the Big Bang during which the universe underwent an extremely rapid exponential expansion. This phase, lasting a fraction of a second, profoundly shaped the structure and evolution of the cosmos. Post-inflation, the expansion of the universe began to decelerate due to the influence of gravitational forces. This decelerating expansion persisted for approximately 9.8 billion years, a period characterized by the dominance of matter and radiation which acted to slow the expansion driven by the initial inflationary impetus [1].

However, contemporary observations reveal a transition from this deceleration to an accelerated expansion, attributed to a mysterious force known as dark energy. Despite extensive research, the precise rate of deceleration during the post-inflationary epoch remains an elusive aspect of cosmological studies. Understanding this rate is crucial as it bridges the early rapid inflationary phase and the current acceleration, providing insights into the dynamics of the universe’s expansion.

This paper aims to estimate the minimum possible deceleration of cosmic expansion post-inflation using a simplified model based on observational data. By considering the observable universe as a spherical volume defined by the particle horizon within the Friedmann-Lemaˆıtre-RobertsonWalker (FLRW) metric, the research applies principles of one-dimensional motion to graphically represent the expansion speed. The model assumes a uniform rate of change in expansion speed, facilitating the calculation of deceleration parameters.

This approach provides a novel and significant contribution to cosmological research by offering a foundational calculation of the minimum deceleration, enhancing our understanding of cosmic expansion dynamics, and setting the stage for future observational and theoretical advancements.

Observational data used in the methodology Radius of the spherical observable universe [2]:

R ≈ (46.508)billion − light-years (1)

To understand why the observable universe is considered spherical, Appendix A. Age of the observable universe [3]:

Reasons for considering a uniform deceleration and acceleration of space-time expansion speed are listed below:

Minimum possible values: Uniform deceleration and acceleration are assumed to derive estimates of the minimum possible deceleration and acceleration of cosmic expansion. These minimum values offer insights into the early stages of cosmic evolution and the transition to accelerated expansion.

Simplification: By assuming uniform deceleration and acceleration, the study simplifies the complex dynamics of cosmic expansion. This simplification allows for a more straightforward mathematical analysis and estimation of the minimum possible deceleration.

Graphical representation: The use of uniform deceleration and acceleration facilitates the graphical representation of the expansion speed over time. This graphical approach aids in visualizing the changes in expansion speed during the post-inflationary epoch.

Foundational calculation: The study aims to provide a foundational calculation of the minimum deceleration of cosmic expansion post-inflation. By considering uniform rates of change in expansion speed, the study establishes a basis for further research and observational refinement in understanding the dynamics of cosmic expansion.

The approach: First of all, we determine the present speed v, at which the observable universe could be expanding. This can be done by applying the Hubble’s Law. Putting the values from Equations (6) and (1), we can use the radius of the observable universe as the proper distance D, which represents how far the expansion may have taken place:

v = H0∗R (8)

v ≈ 1.052 ∗ 109ms⁻¹ (9)

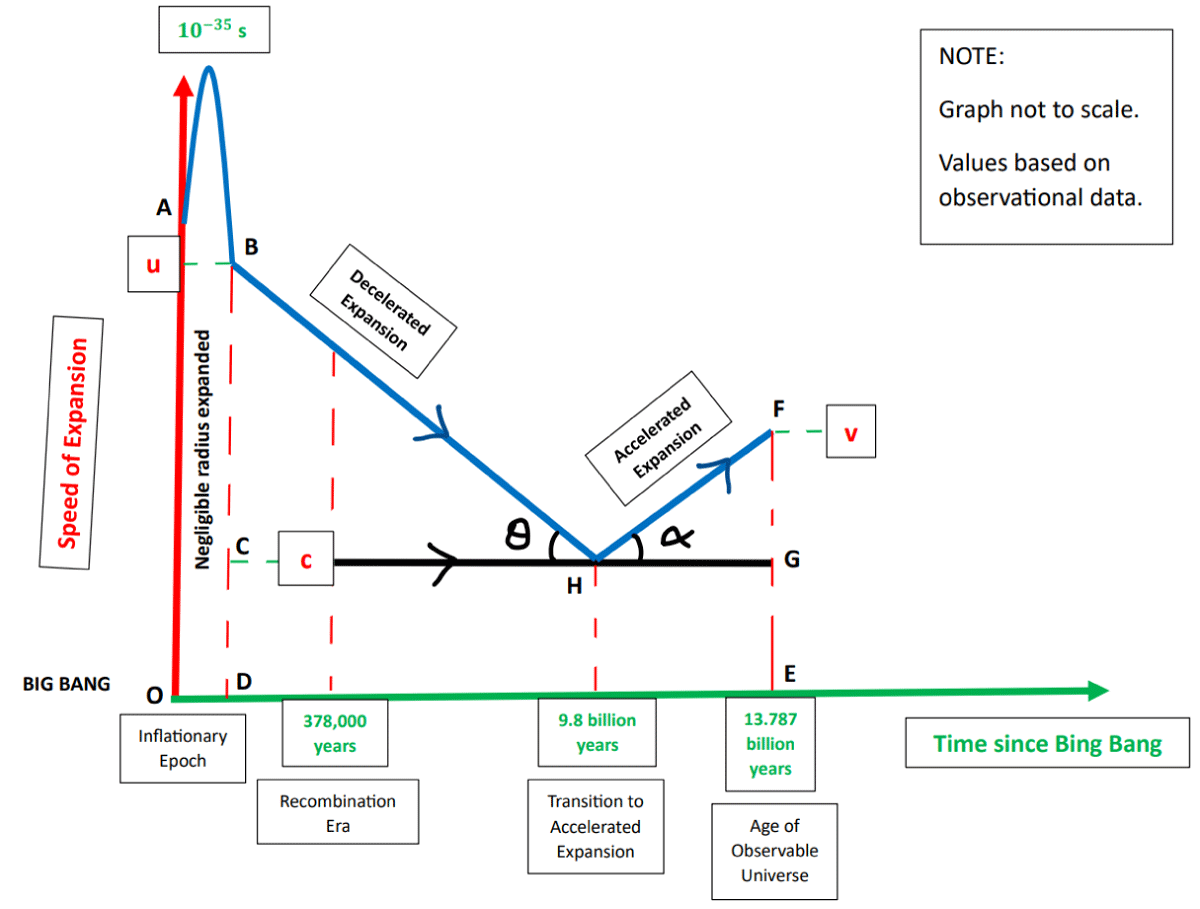
This recession speed exceeds that of light. Nevertheless, this does not contradict the theory of relativity. For a detailed reasoning for the superluminary speed of cosmic expansion, Appendix C. Now, refer to Figure 1 and observe the expected variation in the speed of cosmic expansion with time. The graph also provides a brief overview of the events following the Big Bang. A more detailed picture is given in Appendix B. Our main goal is to determine the initial speed of space-time expansion, denoted as u, immediately after the end of the exponential expansion of the inflationary epoch, marking the onset of gradual deceleration.

It is known that the area under the v-t curve gives the distance. In Figure 1, the total area under the v-t curve represents the total proper distance by which space-time has expanded till yet since the Big Bang. This is equal to the radius of the observable universe, R. Therefore:

R = ABDO + BHC + FHG + CDEG (10)

We must not forget that the area ABDO is the radius of the universe, exponentially expanded, at the time of the inflationary epoch. Let this radius be called ”the epoch radius”:

r_e = ABDO

To estimate the value of epoch radius, we can refer to the period for which it occurred: from 10⁻³⁵ seconds to 10⁻³³ or 10⁻³² seconds, which accounts for a negligible duration of at most 10⁻³² seconds (see Equation (3)). Even if we consider the speed of expansion at inflation to be as high as 10³² ms⁻¹, the epoch radius would reach just 1m, which is negligible as compared to the present radius of the observable universe, R. Various books and articles (like [1] and [8]) also talk about the epoch radius to be much smaller than a meter. Given this extremely small value, we can consider:

r_e ≈ negligible (11)

The areas BHC and FHG form right triangles and the area CDEG makes a rectangle. Now using the Equations (10) and (11), we have:

R ≈ BHC + FHG + CDEG (12)

$R\approx \frac{1}{2}BC.CH+\frac{1}{2}FG.GH+\left(CD.DE\right)$ (13)

$R\approx \frac{1}{2}(BC.CH+FG.GH)+\left(CD.DE\right)$ (14)

Referring to Figure 1, we have:-

BC = u – c (15A)

CH = ta – t_e (15B)

FG = v − c (15C)

GH = T − t_a (15D)

CD = c − 0 (15E)

DE = T − t_e (15F)

or by considering Equation (3),

DE ≈ T (15G)

Substituting all the Equations from (15A) to (15G) into Equation (14), we get:

$R\approx \frac{1}{2}[(u-c).(t_a-t_e)+(v-c).(T-t_a)]+c.T$ (16)

In Figure 1, the uniform (assumed) deceleration of expansion (just after the end of the inflationary epoch) is given by the slope of the v-t graph as follows:

d = tanθ (17)

$d=\frac{u-c}{t_a-t_e}$ (18)

And, the uniform acceleration of expansion (which is occurring since the deceleration stopped) is given by the opposite slope of the v-t graph as follows:

a = tanα (19)

$a=\frac{v-c}{\text{ T}-t_a}$ (20)

Substitute the values, in their respective SI units, from Equations (1), (2), (3), (5), (7), and (9) into Equation (16), and solve for u. After a lengthy calculation, we get:

u ≈ 2 * 10⁹ms⁻¹ (21)

To find the deceleration of expansion speed, we can substitute the values, in their respective SI units, from Equations (21), (5), and (7) into Equation (18). After calculating, we get:

d ≈ 5.51 * 10⁻⁹ms⁻² (22)

Using the same approach, we can find the acceleration of expansion of the observable universe using Equation (20):

a ≈ 5.99 * 10⁻⁹ms⁻² (23)

Just after the end of the inflationary epoch, the initial speed of cosmic expansion, u, obtained in Equation (21), was greater than both c and v:

u > v > c (24)

Also, the deceleration of the initial expansion rate, d, obtained in Equation (22), was smaller than the present acceleration, a, of the expanding universe:

d < a (25)

Note: The calculated values of initial speed, initial deceleration, and present acceleration of space-time expansion provide an estimate of only the minimum possible values. The actual values may be greater.

The study of cosmic expansion has been a central theme in cosmology, with numerous models, theories, and hypotheses proposed to understand the various phases of the universe’s evolution. This discussion will highlight similar works by other scholars that have contributed to our understanding of the deceleration and acceleration phases of cosmic expansion.

1. The Lambda-CDM model: The Lambda Cold Dark Matter model is the standard model of Big Bang cosmology. It posits that the universe is composed of a cosmological constant (Lambda) associated with dark energy, cold dark matter (CDM), and ordinary matter. This model effectively explains the accelerated expansion of the universe observed in recent epochs. Scholars such as Perlmutter et al. (1999) [9] and Riess et al. (1998) [10] provided pivotal observations of Type Ia supernovae, which demonstrated the accelerated expansion and supported the Lambda-CDM model.

2. Deceleration parameters and cosmic dynamics: Various researchers have explored the deceleration parameter (q) to understand the transition from deceleration to acceleration in the universe’s expansion. Studies by Peebles and Ratra (2003) [11] have discussed the cosmological constant problem and the role of dark energy in driving accelerated expansion. Their work highlights the complexities in determining the precise rate of deceleration due to the influence of dark energy and other factors.

3. Scalar field models: Scalar field models, such as quintessence, propose that a dynamic field drives the accelerated expansion of the universe. Caldwell, Dave, and Steinhardt (1998) [12] introduced the concept of quintessence, a scalar field that varies over time and space, offering an alternative to the cosmological constant explanation for dark energy. These models attempt to explain the transition from deceleration to acceleration with varying field strengths over cosmic time.

4. Theories on dark energy: Several alternative theories propose mechanisms for dark energy beyond the cosmological constant. For instance, Copeland, Sami, and Tsujikawa (2006) [13] reviewed various dynamical dark energy models, including k-essence and phantom energy, which provide different perspectives on the late-time acceleration of the universe. These theories aim to address the unresolved aspects of cosmic expansion dynamics, similar to the approach of this paper in estimating minimum deceleration.

5. Modified gravity theories: Modified gravity theories, such as f(R) gravity, suggest alterations to General Relativity to explain cosmic acceleration without invoking dark energy. Starobinsky (1980) [14] and more recent works by Nojiri and Odintsov (2006) [15] have explored how modifications to the Einstein-Hilbert action can lead to accelerated expansion, providing an alternative framework for understanding cosmic dynamics.

The research presented in this paper builds on the foundation laid by these various models and theories, offering a simplified approach to estimate the minimum possible deceleration of cosmic expansion. By focusing on the post-inflationary epoch and utilizing a graphical representation of expansion speed, this study provides a unique contribution to the ongoing discourse on cosmic expansion. Future research can further refine these estimates and explore the implications of the findings in the context of the broader cosmological models discussed.

Limitations

Observational constraints: The calculations are based on observational data, which are subject to uncertainties and limitations inherent in astronomical measurements.

Neglect of complex interactions: The model does not account for interactions between different components of the universe, such as dark matter and dark energy, which can significantly affect the expansion dynamics.

Approximation of epoch radius: The estimation of the epoch radius as negligible may overlook potential subtleties in the inflationary expansion scale, leading to approximations that could affect the accuracy of the results.

Assumption of spherical geometry: The consideration of the observable universe as a perfect sphere based on the FLRW model may not fully capture the actual geometric complexities of the cosmos.

Time frame simplifications: The transition times between different cosmic phases are treated with broad approximations, which may not reflect the precise temporal evolution of the universe’s expansion.

Exclusion of relativistic effects: The model primarily focuses on nonrelativistic aspects of expansion, potentially neglecting relativistic corrections that could influence the calculations.

Potential biases in data sources: Reliance on specific data sets and literature may introduce biases depending on the methodologies and assumptions employed in these sources.

By acknowledging these limitations, this study provides a foundational estimate of the minimum possible deceleration of cosmic expansion post-inflation, inviting further research to refine and expand upon these preliminary findings.

Appendix A

How can we say that the observable universe is spherical when we know about the FLRW Universe being flat?

The FLRW metric a fundamental framework in cosmology based on an exact solution of Einstein’s field equations of general relativity. It describes a homogeneous, isotropic, and expanding (or contracting) universe. The FLRW model assumes that the universe is path-connected but not necessarily simply connected. The metric provides a way to describe the overall geometry and dynamics of the cosmos.

The FLRW metric allows for different spatial curvatures: flat (k=0), spherical (k=1), and hyperbolic (k=-1). These curvatures correspond to different geometric shapes for the universe on large scales (k is the curvature parameter). Specifically: Flat (k=0): The spatial geometry is Euclidean, and the universe expands indefinitely without re-collapsing. Spherical (k=1): The spatial geometry is positively curved, like the surface of a sphere. The universe expands and eventually re-collapses. Hyperbolic (k=-1): The spatial geometry is negatively curved, like a saddle shape. The universe expands forever.

The term “observable universe” refers to the portion of the cosmos from which light has had time to reach us since the beginning of the universe. In the FLRW model, the observable universe is defined by the particle horizon, which is a sphere centered on Earth with a radius equal to the distance light can travel since the Big Bang. The particle horizon depends on the scale factor of the universe a(t) and the cosmic time.

If the FLRW model assumes a spherical curvature (k=1), then the observable universe would indeed be spherical. In this scenario, the particle horizon defines a sphere around us, beyond which we cannot observe any events due to the finite speed of light. However, it’s essential to note that this “spherical” boundary is not a physical surface; it’s a mathematical construct based on the FLRW metric.

Interestingly, even in a flat (k=0) FLRW universe, the observable universe’s boundary remains spherical. This is because the observable limits are determined by the finite age of the universe and the speed of light, not by the spatial curvature. The co-moving distance to the observable universe’s edge remains constant, regardless of curvature.

It’s worth noting that the concept of a spherical observable universe is a mathematical abstraction that helps us understand the limits of our observations within the context of cosmic expansion [16].

Appendix B

What were the events that followed the Big Bang? How did the initial cosmic expansion come down to a decelerating rate? Why then, did it accelerate?

The Big Bang (before which there was no space-time), was immediately followed by the Planck epoch, the inflationary epoch (space-time expanded exponentially), the electroweak epoch, the quark epoch, and the hadron epoch - all within a tiny fraction of a second. Then the lepton epoch occurs for 10 seconds followed by nucleosynthesis for 3 minutes. After that, the radiation-dominated era lasted until 47,000 years and was succeeded by the matter-dominated era, which is continuing till the present. The recombination era happened at approximately 378,000 years, which is shown in Figure 1. After that, the dark ages began until the formation of the first stars and the subsequent formation of galaxies and celestial bodies. Since the inflationary epoch, the universe continued to expand, but at a decelerated rate. This deceleration was transitioned to an acceleration expansion at about 9.8 billion years. Since then, the universe has had an accelerated expansion due to a mysterious dark energy.

Inflationary epoch: The inflationary epoch occurred in the very early universe, shortly after the Big Bang. It is believed to have lasted from approximately 10^-36 seconds to somewhere between 10⁻³³ and 10⁻³² seconds after the Big Bang. During this period, the universe underwent an extremely rapid exponential expansion. The linear dimensions of the early universe increased by a factor of at least 10²⁶ (and possibly much larger), resulting in a volume increase of at least 10⁷⁸. To put this in perspective, expanding an object 1 nanometer (about half the width of a DNA molecule) to approximately 10.6 light-years (about 62 trillion miles) corresponds to a factor of 1026 expansion.

End of inflation: The exact moment when the inflationary epoch ended is not precisely known, but it is estimated to have occurred between 10⁻³³ and 10⁻³² seconds after the Big Bang. As inflation concluded, the universe transitioned to a phase of slower expansion.

Recombination era: As the universe cooled down, protons and neutrons began to combine into ionized atoms of hydrogen (and eventually some helium). These ionized atoms attracted electrons, turning them into neutral atoms. The crucial point: Neutral atoms allowed light to travel freely for the first time. Before this, the universe was opaque because light was constantly scattering off free electrons. However, it would still be some time (perhaps up to a few hundred million years post-Big Bang) before the first sources of light (such as stars) would form.

Cosmic deceleration: After inflation, the universe continued to expand, but at a decelerated rate. During the subsequent phases, such as the radiation-dominated era and the matter-dominated era, the expansion rate gradually decreased due to gravitational effects. The matter and radiation present in the universe influenced the overall dynamics, leading to a slower expansion.

Accelerated expansion: Interestingly, in more recent times (around the last few billion years), observations have revealed that the universe is now experiencing an accelerated expansion. This acceleration is attributed to the mysterious dark energy, which counteracts the gravitational pull and causes the expansion rate to increase over time [5].

Appendix C

How can the recession speed of cosmic expansion exceed the speed of light? Doesn’t it violate general relativity?

According to Hubble’s law, the expansion of the universe causes distant galaxies to recede from us faster than the speed of light. However, the recession speed associated with Hubble’s law, defined as the rate of increase in proper distance per interval of cosmological time, is not a velocity in a relativistic sense. Moreover, in general relativity, velocity is a local notion, and there is not even a unique definition for the relative velocity of an object at a cosmological distance.

As the expansion of the universe is accelerating, it is projected that most galaxies will eventually cross a type of cosmological event horizon where any light they emit past that point will never be able to reach us at any time in the infinite future, because the light never reaches a point where its ”peculiar velocity” towards us exceeds the expansion velocity away from us [17].

1. Fraknoi A, Morrison D, Wolff S. Astronomy 2e ( hardcover, Full Color). Independently Published; 2023.
2. Gott JR 3rd, et al. A map of the universe. Astrophys J. 2005 May;624(2):463–484.
3. Aghanim N, Akrami Y, et al. Planck 2018 results: Vi. cosmological parameters. Astron Astrophys. 2020 Sep;641
4. Tanabashi M, Hagiwara K, et al. Review of particle physics. Phys Rev D. 2018 Aug;98(3):030001.
5. Ryden B. Introduction to Cosmology. Cambridge University Press; 2017.
6. NASA Hubble Mission Team. Nasa’s Hubble rules out one alternative to dark energy; 2011.
7. Stein V. What is the speed of light? 2023.
8. Mike and Tamara. Universe after inflation; 2007.
9. Perlmutter S, et al. Measurements of omega and lambda from 42 high-redshift supernovae. Astrophys J. 1999;517:565–586.
10. Riess AG, et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron J. 1998;116:1009–1038.
11. Peebles PJE, Ratra B. The cosmological constant and dark energy. Rev Mod Phys. 2003;75(2):559–606.
12. Caldwell RR, Dave R, Steinhardt PJ. Cosmological imprint of an energy component with general equation of state. Phys Rev Lett. 1998;80(8):1582.
13. Copeland EJ, Sami M, Tsujikawa S. Dynamics of dark energy. Int J Mod Phys D. 2006;15(11):1753–1936.
14. Starobinsky AA. A new type of isotropic cosmological model without singularity. Phys Lett B. 1980;91(1):99–102.
15. Nojiri S, Odintsov SD. Introduction to modified gravity and gravitational alternative for dark energy. Int J Geom Methods Mod Phys. 2006;4(1):115–146.
16. Vlahovic B. Spherical shell cosmological model and uniformity of cosmic microwave background radiation. 2012 Jul.
17. Loeb A. Long-term future of extragalactic astronomy. Phys Rev D. 2002 Jan;65(4):047301.