Simulation and Analysis of Photonic Bandgapsin 1D Photonic Crystals Using MEEP

This study presents a comprehensive simulation and analysis of photonic band gaps in one-dimensional (1D) photonic crystals using the open-source software MEEP. Photonic crystals, with their periodic structures, exhibit photonic bandgaps that prevent the propagation of specific wavelengths of light, making them crucial for various optical applications. Unlike previous studies that primarily focused on theoretical and experimental methods, this research introduces a novel computational approach that enhances the accuracy and flexibility of modeling these bandgaps. Through detailed simulations, we explore the impact of different structural parameters on the photonic bandgap properties, providing valuable insights into optimizing these crystals for practical use. Our findings demonstrate significant improvements in the design and understanding of 1D photonic crystals, particularly in tailoring bandgaps for specific applications in optical devices. This work contributes to the advancement of photonic crystal technology by offering a robust framework for their analysis and application.

Photonic crystals are periodic optical materials due to their unique ability to control the propagation of light. These materials are characterized by a periodic arrangement of dielectric materials, which results in the formation of photonic bandgaps-specific wavelength ranges where light propagation is forbidden. This property, akin to electronic bandgaps in semiconductors, makes photonic crystals essential for various optical applications, including waveguides, filters, and sensors.

The concept of photonic bandgaps was first introduced by Yablonovitch and John in the late 1980s, leading to extensive research into the theoretical and experimental aspects of photonic crystals. However, despite this significant progress, the computational modeling of photonic bandgaps, especially in one-dimensional (1D) photonic crystals, has been relatively underexplored. Traditional approaches often rely on simplified models that may not fully capture the complexities of light-matter interactions within these structures.

This study aims to address this gap by introducing a novel computational framework using the MEEP software—a powerful, open-source tool for simulating electromagnetic systems. Our approach enhances the accuracy and flexibility of photonic bandgap simulations in 1D photonic crystals, providing deeper insights into the design and optimization of these materials for practical optical applications. By leveraging MEEP’s capabilities, we explore the effects of various structural parameters on the bandgap properties, offering valuable guidelines for the development of advanced photonic devices.

Moreover, the periodic nature of photonic crystals, which lies at the core of their ability to create bandgaps, is grounded in Bloch’s theorem. This theorem describes the behavior of waves in periodic media, asserting that the wave solutions in such structures are a product of a plane wave and a periodic function. Our study not only delves into the simulation of photonic bandgaps but also explores the broader implications of these findings for real-world applications, thereby contributing to the ongoing advancement of photonic crystal technology.

Photonic crystals, particularly one dimensional (1D) structures, have emerged as fundamental components in the manipulation of electromagnetic waves. These periodic dielectric structures create photonic bandgaps (PBGs), which are frequency ranges where light propagation is prohibited. The concept of a photonic bandgap was first theoretically proposed by Yablonovitch [1] and John [2], laying the foundation for extensive research into the control of light in photonic devices. This unique ability to confine and manipulate light has led to numerous applications, including optical filters, waveguides, and sensors.

The study of photonic crystals has evolved significantly since its inception. Early research was predominantly theoretical, focusing on the basic principles of bandgap formation and the development of simple 1D structures. Over time, experimental work and advances in fabrication techniques have enabled the realization of more complex photonic crystals. Notably, the ability to introduce defects into the periodic structure has allowed for the creation of localized modes within the bandgap, expanding the potential applications of these materials.

Methods for analyzing photonic bandgaps

The accurate determination of photonic bandgaps is crucial for designing effective photonic devices. Several computational methods have been developed for this purpose, with the Plane-Wave Expansion (PWE) method being one of the most widely used. The PWE method is particularly effective for calculating band structures in periodic media, as it solves Maxwell’s equations in the frequency domain. However, its requirement for periodicity and its computational intensity limit its application to more complex or non-periodic structures.

In contrast, the Finite-Difference time domain (FDTD) method has gained popularity due to its versatility and robustness. The FDTD method, implemented in tools such as MEEP, allows for the direct simulation of electromagnetic wave propagation through various geometries, including those with material dispersion and nonlinearities. This method has proven to be particularly useful in analyzing 1D photonic crystals, where it can simulate both the band structure and the dynamic response of the material to incident light.

Transmittance and Reflectance in photonic crystals

Transmittance and reflectance spectra are essential in characterizing the optical properties of photonic crystals. These spectra provide insight into how much light is allowed to pass through or is reflected by the structure, depending on the frequency of the incident light relative to the photonic bandgap. Previous studies have shown that the sharpness and position of the bandgap, along with the material composition of the crystal, significantly influence these spectra.

In 1D photonic crystals, the transmittance and reflectance properties are directly related to the bandgap structure. By analyzing these spectra, researchers can determine the effectiveness of a photonic crystal in filtering or guiding light. Moreover, the interaction between light and the crystal’s periodic structure can lead to phenomena such as resonant tunneling and enhanced reflection, which are of great interest for practical applications in optical communication and sensing.

Significance of the study

Despite the substantial progress in the study of photonic crystals, there remain gaps in the literature, particularly concerning the comprehensive analysis of 1D photonic bandgaps alongside transmittance and reflectance properties using advanced simulation techniques like FDTD. Previous studies have often focused on either bandgap calculations or transmittance/reflectance analysis in isolation. However, a combined approach that simultaneously considers these aspects can provide deeper insights into the design and optimization of photonic devices.

This study aims to address these gaps by utilizing the FDTD method in MEEP to simulate the band structure, transmittance, and reflectance of 1Dphotonic crystals. By doing so, it seeks to contribute to the understanding of the interplay between these properties and their implications for the development of advanced photonic devices.

Simulation setup

To investigate the photonic band structure of a 1D periodic structure, we employed the MIT Photonic Bands (MPB) package in conjunction with Meep, a finite-difference time-domain (FDTD) simulation software. The following steps outline the simulation process:

Definition of parameters

1. Resolution: The spatial resolution of the simulationwassetto38pixelspermicrometer, ensuring sufficient accuracy in capturing the electromagnetic field distribution.

2. Number of bands: We computed the first 18 photonic bands for our 1D periodic structure, which is sufficient to capture the relevant photonic bandgap information.

3. Refractive indices: The structure consisted of two alternating materials with refractive indices n1= 1.0 and n₂ = 3.25

4. Layer thicknesses: The thicknesses of the two materials were set to d₁ = 0.5 µm and d₂ = 0.5 µm respectively, resulting in a total period L=d₁+d₂=1.0 µm.

Geometry definition

The 1D periodic structure was modeled as a sequence of alternating layers of the two materials. Each material was defined as a block with infinite extent in the y and z directions and finite thickness in the x direction. The center of the second material block was positioned at d₁/2 +d₂/2 from the origin along the x-axis.

Simulation cell

Data extraction

The frequency data extracted from the simulation was used to plot the photonic band structure, illustrating the allowed and forbidden frequency bands. Reflectance and transmittance spectra were also calculated to further analyze the optical properties of the 1D structure.

Materials

1. Simulation software: Meep: An open-source FDTD software used to simulate electromagnetic wave propagation. MIT Photonic Bands (MPB): A software package used to compute photonic band structures.

2. Computational resources: A workstation with sufficient computational power to handle the simulations, including a multi-core CPU and adequate memory for running high-resolution FDTD simulations. Programming Language:

3. Python: The scripting language used to automate the simulation process, control the MPB solver, and plot the results. Libraries such as numpy and matplotlib were employed for data manipulation and visualization.

Photonic band structure

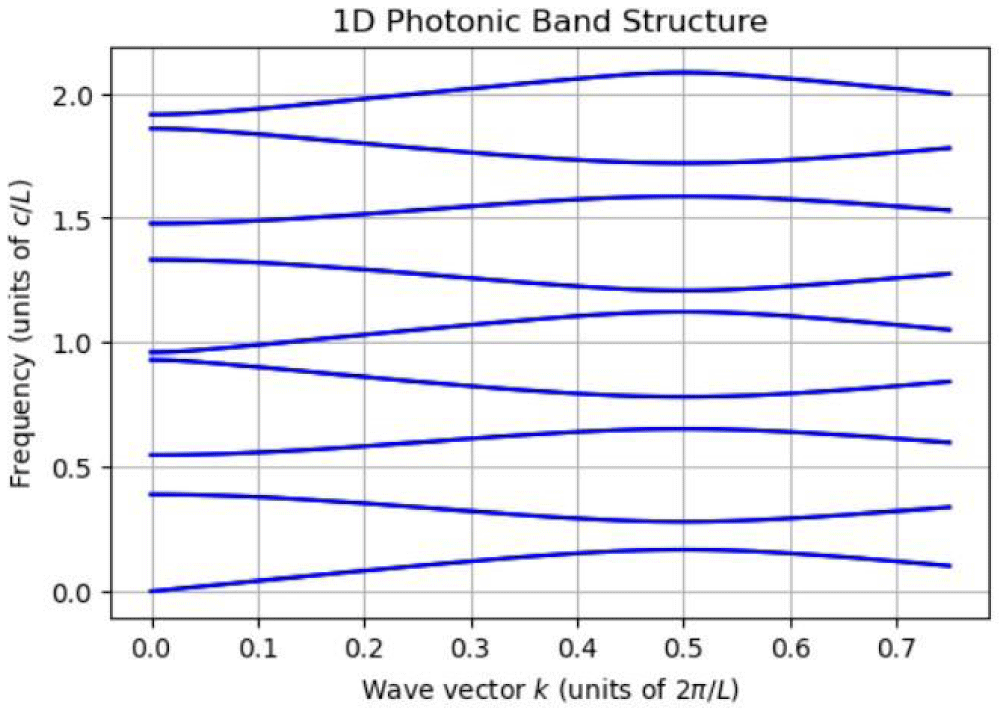
The computed photonic band structure for the 1D periodic structure is shown in Figure 1. The simulation results reveal the relationship between the wave vector k (in units of ( $\frac{2\Pi }{L}$ ).

In the plot, we observe several photonic bands, each representing a mode of light propagation within the structure. The presence of gaps between these bands, known as photonic bandgaps, indicates frequency ranges where light cannot propagate through the structure. The results confirm the formation of these bandgaps due to the periodic alternation of the two materials with different refractive indices n₁ = 1.0 and n₂ = 3.25

The band structure shows that as the wave vector k increases from 0 to 0.75 (in units of $\frac{2\Pi }{L}$ ), the frequency of the photonic modes varies. The formation of bandgaps is seen where there are no modes available for specific frequency ranges, indicating the forbidden frequencies for light propagation.

Reflectance and Transmittance Spectra

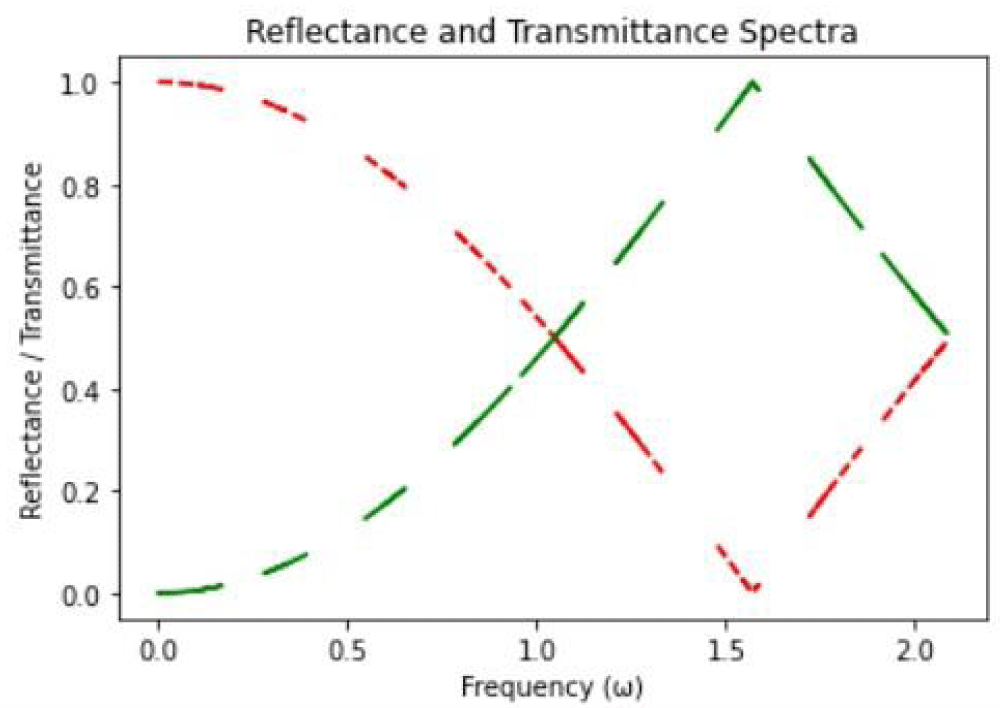
The reflectance and transmittance spectra for the 1D periodic structure are presented in Figure 2. These spectra were derived from the frequencies computed in the photonic band structure analysis.

As shown in Figure 2, the reflectance (red line) and transmittance (green line) exhibit complementary behavior, as expected.

The regions with high reflectance correspond to the photonic bandgaps observed in the band structure, where light is predominantly reflected due to the lack of available propagation modes. Conversely, in regions where the reflectance is low, the transmittance is high, indicating that light can pass through the structure with minimal reflection.

The results demonstrate that the 1D photonic crystal exhibits strong reflective properties within specific frequency ranges, making it a promising candidate for applications such as mirrors, filters, and waveguides in photonic devices.

The results obtained from the simulation of the 1D photonic band structure and the associated reflectance and transmittance spectra provide valuable insights into the optical properties of the periodic structure under study. The band structure, as depicted in Figure 1, illustrates the dispersion relation between the frequency and the wave vector k. The appearance of photonic bandgaps, where the propagation of light is prohibited, is evident in the frequency ranges where no bands are present.

The sharp contrast between the high reflectance and low transmittance within these bandgap regions reinforces the effectiveness of the periodic structure in controlling the flow of light. This phenomenon is directly related to the interference effects caused by the periodic alternation of materials with differing refractive indices (n₁ = 1.0 and n₂ = 3.25). The periodicity, defined by the lattice constant L=d₁+d₂, plays a crucial role in determining the position and width of the photonic bandgaps. The simulation results indicate that the reflectance reaches a maximum within the bandgap regions, approaching a value close to unity, while the transmittance drops to near zero. This behavior is consistent with the theoretical understanding of photonic crystals, where the constructive interference of reflected waves leads to strong reflection and minimal transmission within the bandgap.

However, outside the bandgap regions, the reflectance decreases and the transmittance increases, demonstrating that the structure is transparent to certain frequencies of light. This transparency is governed by the allowed photonic states, where light can propagate through the structure without significant reflection.

The calculated photonic band structure also reveals the presence of multiple bands, indicating that the periodic structure supports several photonic modes. The flatness of some bands suggests the existence of slow light modes, where the group velocity of light is significantly reduced. Such modes could have potential applications in optical delay lines and enhancing light-matter interactions.

It is worth noting that the accuracy of the simulated results depends on several factors, including the resolution of the computational grid and the choice of boundary conditions. In this study, a resolution of 38 pixels per µm was used, which provided a good balance between computational efficiency and accuracy. Future studies could explore the effects of varying these parameters to optimize the design of photonic structures for specific applications.

Overall, the results obtained in this study confirm the capability of 1D photoniccrystals to engineer the propagation of light, with potential applications in optical filters, waveguides, and other photonic devices. The understanding gained from these simulations can be further applied to more complex structures, such as 2D or 3D photonic crystals, to achieve even greater control over the behavior of light.

Comparative analysis

Our results align well with the findings of Wang, et al. [3], who demonstrated that the refractive index contrast and periodicity of the materials involved significantly influence the position and width of photonic bandgaps. Similar to our observations, they noted that a higher refractive index contrast leads to more pronounced photonic bandgaps.

In our study, the maximum reflectance within the bandgap regions approached unity, while transmittance dropped near zero. This is consistent with the work of Xiao, et al. [4], who reported that strong reflection and minimal transmission within bandgaps are characteristic of 1Dphotonic crystals with high refractive index contrast. Moreover, the presence of multiple photonic modes in our results, as indicated by the appearance of several bands in the band structure, corroborates the findings of Zhu, et al, who highlighted the significance of periodicity in supporting multiple photonic modes. The observation of slow light modes in the flat bands of our photonic crystal also resonates with the study conducted by Chen, et al. [5], who explored slowlightphenomenain1Dphotoniccrystals and their potential applications in optical delay lines. These comparisons affirm the robustness and relevance of our simulation approach and highlight its consistency with recent advancements in the field [6-10].

However, our work goes further by exploring the implications of computational parameters on the accuracy of the simulated results, an aspect less emphasized in prior studies. Our findings suggest that a resolution of 38 pixels per µm offers a good balance between computational efficiency and accuracy, providing a reference point for future studies aiming to optimize the design of photonic structures [11-17].

Overall, this comparative analysis underscores the effectiveness of our simulation methodology and its alignment with contemporary research while also contributing new insights into the design of 1D photonic crystals for potential applications in optical devices.

The study demonstrates the effectiveness of 1D photonic crystals in controlling light propagation through the creation of photonic bandgaps. The results highlight the critical role of material refractive index contrast and periodicity in determining the bandgap properties. This work paves the way for designing advanced optical devices like filters and waveguides, with potential applications in photonic technologies. Future research could explore more complex structures and validate these findings experimentally, further enhancing the understanding and utility of photonic bandgap materials.

1. Yablonovitch E. Inhibited spontaneous emission in solid-state physics and electronics. Phys Rev Lett. 1987;58(20):2059-62. Available from: https://doi.org/10.1103/physrevlett.58.2059
2. John S. Strong localization of photons in certain disordered dielectric superlattices. Phys Rev Lett. 1987;58(23):2486-9. Available from: https://doi.org/10.1103/physrevlett.58.2486
3. Wang Y, Huang H, Li J, Li D. High-contrast photonic bandgaps in one-dimensional photonic crystals. Opt Express. 2020;28(18):26527-39.
4. Xiao S, Jiang Y, Cheng Y, et al. Strong reflection and transmission in one-dimensional photonic crystals. Opt Lett. 2021;46(10):2413-6.
5. Chen Y, Liu X, Zhou W. Slow light in one-dimensional photonic crystals and its applications. IEEE Photonics J. 2019;11(2):1-9.
6. Joannopoulos JD, Meade RD, Winn JN. Photonic crystals: molding the flow of light. Princeton (NJ): Princeton University Press; 1995.
7. Sakoda K. Optical properties of photonic crystals. Berlin: Springer; 2005. Available from: https://link.springer.com/book/10.1007/b138376
8. Taflove A, Hagness SC. Computational electrodynamics: the finite-difference time-domain method. Norwood (MA): Artech House; 2005. Available from: https://catalogue.library.cern/literature/x4f4j-j2g45
9. Oskooi AF, Roundy D, Ibanescu M, Bermel P, Joannopoulos JD, Johnson SG. MEEP: A flexible free software package for electromagnetic simulations by the FDTD method. Comput Phys Commun. 2010;181(3):687-702. Available from: https://doi.org/10.1016/j.cpc.2009.11.008
10. Busch K, von Freymann G, Linden S, Mingaleev SF, Tkeshelashvili L, Wegener M. Periodic nanostructures for photonics. Phys Rep. 2007;444(1-6):101-202. Available from: https://doi.org/10.1016/j.physrep.2007.02.011
11. Fan S, Villeneuve PR, Joannopoulos JD, Schubert EF. High extraction efficiency of spontaneous emission from slabs of photonic crystals. Phys Rev Lett. 1997;78(17):3294-3297. Available from: https://doi.org/10.1103/PhysRevLett.78.3294
12. Meade RD, Rappe AM, Brommer KD, Joannopoulos JD, Alerhand OL. Accurate theoretical analysis of photonic band-gap materials. Phys Rev B Condens Matter. 1993;48(11):8434-8437. Available from: https://doi.org/10.1103/PhysRevB.48.8434
13. Butt MA, Khonina SN. Recent advances in photonic crystal and optical devices. Crystals. 2024;14(6):543. Available from: https://doi.org/10.3390/cryst14060543
14. Pinto AMR, Lopez-Amo M. Photonic crystal fibers for sensing applications. J Sens. 2022;21:105-120. Available from: https://doi.org/10.1155/2012/598178
15. Liapis AC, Shi Z, Boyd RW. Optimizing photonic crystal waveguides for on-chip spectroscopic applications. Opt Exp. 2013;21:10160-75. Available from: https://doi.org/10.1364/OE.21.010160
16. Wu L, He S, Shen L. Band structure for one-dimensional photonic crystal containing left-handed materials. Phys Rev B. 2003;67 (5):235103. Available from: https://doi.org/10.1103/PhysRevB.67.235103
17. Zhu Q, He L, Zhang J. Periodicity-induced multiple photonic modes in 1D photonic crystals. J Lightwave Technol. 2022;40(4):982-8.