Precessional Motion Emerging from Relativistic Component of External Force

The external force in the relativistic equation of motion can be separated into two components: F_r and F_p. The first is expressed by the physical force divided by the square of the relativistic Lorentz factor, i.e γ². This force dominates for non-relativistic velocities and vanishes for velocities approaching the speed of light c. On the other hand, the second term increases from zero with increasing velocity and dominates for velocities close to c. It is then a purely relativistic component. The characteristic feature of this component is its zero power, F_p . v = 0, but it is responsible for the relativistic precession. The effect was confirmed by numerical solutions of the equation of motion. Relativistic formulas for the precession frequency for point objects moving in selected fields of central forces were also derived analytically. It has been shown that for weak gravitational interactions, the correction for relativistic precession is small, negligibly small for Earth, and relatively small, though measurable, for Mercury. In turn, for the microworld and electrostatic forces (e.g., for the hydrogen atom), relativistic precession can fundamentally affect the movement of the electron.

The relativistic equation of motion takes the form:

$m\frac{\text{d}v}{\text{d}t}=F-\frac{F\cdot v}{\alpha }v$ (1)

Where α is the linear energy-mass ratio and for vacuum is α = c², where c is the speed of light in a vacuum. This equation is derived both within special relativity theory (STR) [1] and within a recently proposed theory based on the assumptions of equivalence of mass and energy and the classical equation of motion of systems with variable mass [2-4].

When deriving Equation (1) we use the commonly known relation of relativistic mass and energy as follows:

E = mc² (2)

The relation (2) is confirmed experimentally and causes the mass of a relativistic object to increase with its energy and, thus, with the speed of motion. So, we are dealing with objects of variable mass. On the other hand, the classical equation of dynamics for systems with variable mass reduces to the following equation:

$\frac{\text{d}p}{\text{d}t}=F$ (3)

which results from the Meshchersky equation (also known as the rocket equation) written for the laboratory (LAB) system, in which the increasing relativistic mass rests [2].

A good classic analogue of Equation (3) is a barge pulled by force F, onto which the sand is falling from above at a zero horizontal velocity. The same applies to the description of the movement of a barge, which increases its mass by taking in water. Under this new theory, c is the critical speed for any object, including light, traveling in a vacuum.

As has been shown [3], starting with equations (3) and (2) and using the definition of the power supplied to a moving system, we arrive at equation (1). The solution of Equation (1) for the velocities < c, is the relativistic relationship between mass and energy expressed by the following formulas [1]:

$E(v)=E_0\gamma =\frac{E_0}{\sqrt{1-{\left(\frac{v}{c}\right)}^2}}$

$m(v)=m_0\gamma =\frac{m_0}{\sqrt{1-{\left(\frac{v}{c}\right)}^2}}$ (4)

Relation (4) is sufficient to derive all relations known in special relativity [e.g., 5]. The γ factor is a commonly used relativistic factor equal to $\gamma ={\left(1-\frac{v^2}{c^2}\right)}^{-1/2}$

Summing up this short introduction, we can treat Equation (1) as the result of applying STR or writing the equation of dynamics for an object with variable mass, which is proportional to the total energy of this object. These two approaches lead to identical equations of motion for objects moving at subluminal speeds. The first approach requires the additional assumption that the speed of light is constant and not to be exceeded and that it takes the value of c in vacuum. The second approach treats c2 as a proportionality constant between mass and energy. c itself is, in turn, a critical value for the speed to which a particle, including light, can approach arbitrarily. For a velocity approaching c, both the object's energy and its mass are singular and tend to infinite values.

A good solution may be the postulative adoption of Equation (1) as a relativistic equation of dynamics without additional assumptions about the constant c. The extensive collection of solutions to Equation (1) includes all cases described by STR as well as those additional characteristics for systems with variable mass.

In the following, we will use Equation (1) to describe the phenomenon of precession, which is closely related to the relativistic description of motion. One of our goals is to reproduce the result of perihelion advance for Mercury. However, to our knowledge, precession was not fully associated and explained with special relativity, occurring only in general relativity [6-12]. The famous experimental verification of Einstein’s general relativity theory was to confirm an additional contribution to the orbit (perihelion) precession of Mercury [13]. In the second half of the twentieth century, several of the so-called post-Newtonian gravity theories tried to obtain the exact result of Mercury's precession rate. Many attempts focused on introducing a 'relativistic' gravitational potential to the Lagrangian of the system (making the potential similar to what is known in general relativity) [14,15]. In [16] the notion of relativistic momentum was used, which reproduced only 1/6 of the observed precession. In [17,18] the concept of cogravity was used to explain general relativity phenomena without using general relativity. Different approaches to relativistic mass (assumed to act as gravitational mass) appeared in [19,20]. Derivations including gravitational and rotational time dilation effects (special relativity effect) in the Schwarzschild metric (general relativity quantity) appeared to reproduce the precession up to the same precision rate as known in general relativity itself [16,21,22]. The full correctness of the approaches briefly discussed above is under debate. We show that the precession is the result of STR itself. For simplicity, we will deal with the description of motion for the simplest object, which is a material point placed in the field of central forces. It was also very recently shown that the precession effect appears purely in Newtonian physics of planetary motion, after including the effect of planet mass in the two-body problem, and for Mercury, the prediction meets the exact value surprisingly well [22]. The prediction falls down for other planets because multi-body interaction needed to be included. In our paper, the effect of the mass of Mercury is neglected. We manage to reproduce 1/3 of the precession predicted by general relativity.

We also show how large the precession effect is for microworld particles, like an electron in a hydrogen atom. We show that directly from the relativistic equation of motion (in special relativity) the effect of precession emerges. We do not include by hand other effects, like time dilation or special design of the interaction potential. To our knowledge, it is a unique result. Analytical and numerical results were obtained for the gravitational force. Earth and Mercury orbiting the Sun, and electrostatic force: electron in hydrogen atom.

Precession equation for a point object

Using vector relations, the dynamics equation (1) can be written in the form [4]:

$m\frac{\text{d}v}{\text{d}t}=F\left(1-\frac{v^2}{c^2}\right)-\frac{v\times (v\times F)}{c^2}=F_{\text{r}}+F_{\text{p}}$ (5)

where:

$F_{\text{r}}=F/{\gamma }^2$ (6)

$F_{\text{p}} =-\frac{\text{v}\times (v\times F)}{c^2}$ (7)

The force F_r is a relativistically renormalized real force F. The ratio of the two forces depends on the speed of the body. For small velocities, the force F_r is equal to the force F and the description of the motion is fully classical, while the force F_p is negligibly small. For relativistic velocities, the value of the force F_r decreases and its significance for the description of motion becomes negligibly small. If the force F is a central force, e.g. gravitational or electrostatic, then under its influence the classical trajectory of a spatially limited motion is a circle or an ellipse. For circular motion, the components F_r and F_p are parallel to each other. The appearance of the parameter γ² introduces the dependence of the force on the velocity, which results in the instability of the orbit. The movement takes place in one plane with the characteristic torsion of the orbit, orbit precession.

In turn, F_p is a vortex force that does not supply power to the system because it is always perpendicular to the velocity vector, v, but is responsible for the phenomenon of precession. In addition, this force component depends on the speed, which causes characteristic blurring of the orbit. For velocities approaching c, the force F_r disappears, and the force F_p leads to simple stable solutions in the form of circular or rectilinear motion. For intermediate speeds, there is a combination of many forms of motion, whose description is very complicated. In total, in the orbit plane, the blurring of orbits is clearly visible in numerical solutions for the sum of the forces F_r+ F_p, but this case is not the subject of the presented work. Our interest is orbital precession caused by the force F_p, the importance of which increases with the increase in particle velocity at the expense of motion governed by the decreasing force F_r. The motion of the body transforms from an elliptical motion to a circular motion. The equation of motion in this approximation takes the form:

$m\frac{\text{d}v}{\text{d}t}=F_{\text{p}}=-\frac{v\times (v\times F)}{c^2}$ (8)

This can also be written in the following form:

$\frac{\text{d}v}{\text{d}t}={\omega }_{\text{p}}\times v$ (9)

Where ω_p is the angular frequency vector (its value acts as precession’s frequency), and is equal to:

${\omega }_{\text{p}}=\frac{v\times F}{m{c}^2}$ (10)

During this phenomenon, the force F_p does not do work, so the kinetic energy is conserved, and the velocity of the body does not change its value. Equation (9) is the classical equation for the precession of the velocity vector, and the angular precession frequency is given by Equation (10).

Selected examples of angular precession motion for central forces acting on point objects

The best-known example of the precession force is the Lorentz force of the magnetic field acting on a moving charge. As was shown in [3], to derive the magnetic force, the relativistic dynamics equation (1) should be generalized to the case of moving force sources (e.g., electrons moving in a conductor with an electric current; velocity of the moving force source is denoted v₀):

$m\frac{\text{d}v}{\text{d}t}=F-\left[F\cdot \left(v-v_0\right)\right]\frac{v}{c^2}$ (11)

and then the part of the precession force F_p depending on the density of electric current carriers should be separated. The obtained equations allow one to define the magnetic field originating from the resultant electric field, which is the sum of two competing components: one from moving electrons and the other from positive ions resting in the LAB system (for details, see [3]). The resulting magnetic field is then given by the formula:

$B=\frac{v_e\times E_{-}}{c^2}$ (12)

where v_e is the velocity of moving electrons, and E- is the electric field generated by the electrons in a conductor. This spectacular phenomenon of the formation of a magnetic field from the superposition of electric fields is dominant in the case of electric field zeroing in the LAB system.

In the following, we present some less spectacular occurrences of precession phenomena for both gravitational and electrostatic central forces. This time, the relativistic effects of the precession force are only a correction to the classical gravitational or electrostatic interactions.

In the case of the gravitational field, an unstable solution appears related to the precession of the orbit, which changes its periapsis (perihelion for the Solar System), but the position of the orbit itself remains in a plane perpendicular to the constant angular momentum vector. For the planets of the solar system, the relativistic precession is very small, and mostly it is only a minor correction to the classical precession associated with the multibody interaction or the size of the planet and its nonsphericality [7-12].

An example of the movement of the planet in a gravitational field

The strength of the gravitational field for a circular orbit is given by Newton's formula:

$F=G\frac{Mm}{r^2}$ (13)

This force is perpendicular to the velocity: $\left|v\times F\right|=vF$ and the period of motion $T=2\pi r/v$ , which gives the expression for the precession angular frequency after substituting for Equation (10):

${\omega }_{\text{p}}=\frac{4{\pi }^{2}GM}{v{c}^2{T}^2}$ (14)

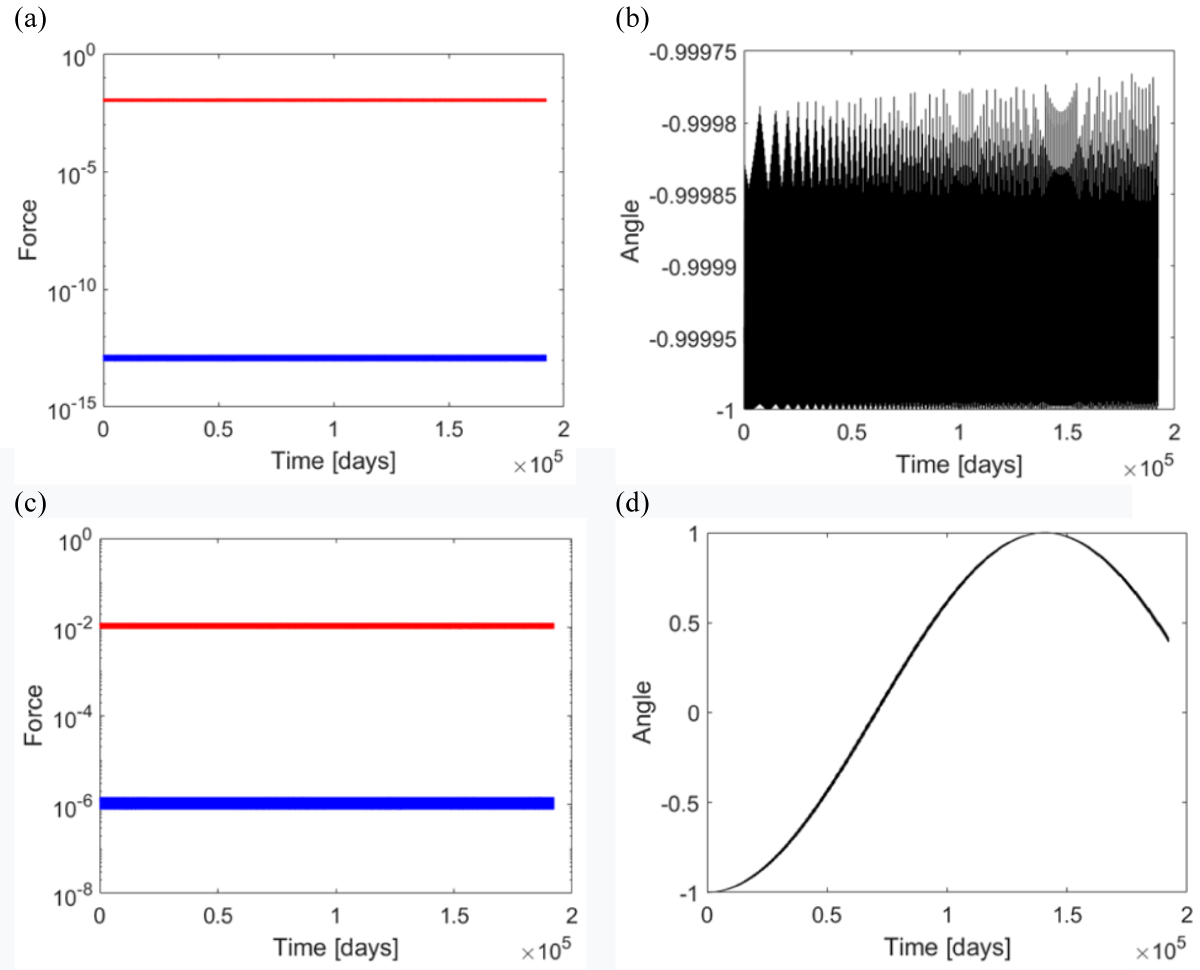
Formula (14) can be used to calculate the precession angular frequency for planets, as will be shown for Earth and Mercury in the following examples. In Figures 1 and 2 the results of numerical calculations for the central force are shown. From Figure 1 we see how important the precession component of the external force becomes with increasing velocity of an object. In our simulation we varied the speed of light, c, and two examples are shown for c=300,000 km/s in subfigures (a)-(b) and c=100 km/s for subfigures (c)-(d), whereas the actual velocity of an object remained constant and equal to the real orbital velocity of Moon in perigee, which is 1.089 km/s. For low velocities, we observe a very large discrepancy of F_r and F_p of 11 orders of magnitude (subfigure (a)), what results in no orbit’s precession, as shown in subfigure (b) – angle of the orbit’s axis varies by a negligible amount in time. The situation is drastically different for high velocities (subfigures (c)-(d) for the ratio, v/c ≈ 0.01), where the discrepancy in force’s components is relatively small (4 orders of magnitude), and orbit’s precession is evident. In this case, it is about 3 · 10⁵ days.

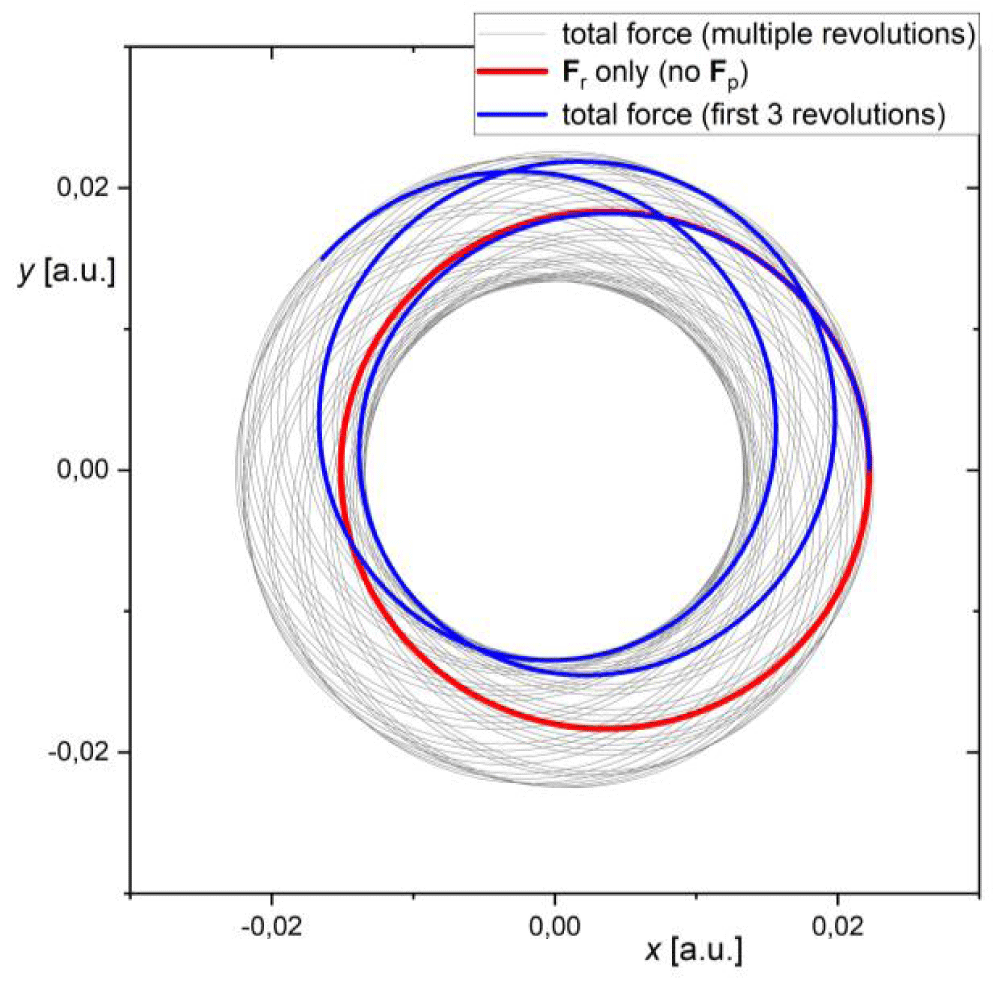
Similar conclusions can be drawn from Figure 2. Here, results of numerical simulations of the motion of a point mass in a central force field from a point source mass on an elliptical orbit are shown. The starting velocity and periapsis radius are chosen arbitrarily and reflect no physical system. From Figure 2 we see that the orbit’s precession emerges only due to the F_p component of the central force. If only F_r component is included in the simulation, the stable elliptical orbit is only seen with no precessional motion. Only including two components can result in an orbit’s precession. For better clarity, the orbit’s shape is highlighted in red for the first 3 revolutions. These two examples in Figures 1 and 2 show how much the F_p component of the central force is responsible for the emerging orbit’s precession.

Precession of orbital precession for earth

To estimate the precession of the Earth, we insert the following values into equation (14): M = 2 . 10³⁰ kg (solar mass), T = 365 days = 3.15 · 10⁷ s, v = 29.78 km/s ≈ 3 · 10⁴ m/s (average speed of the Earth in orbit around the Sun).

Inserting the above data into (14) we get the Earth's precession period of 100 million years, which is much too much compared to the observation result of 26,000 years. Therefore, the approximation of the point mass for Earth leads to an insignificant relativistic correction. The nonspherical shape of Earth and interactions with both the Moon and the Sun are responsible for the phenomenon of classical precession.

Mercury’s precession

For Mercury, the effect of relativistic precession is more visible. In the calculations, a significantly larger eccentricity compared to a circular orbit should be considered. However, if we approximate the formula for force by: $F=\frac{GMm}{r_{\text{av}}{}^2}$ , where r_av is related to the period and average velocity on the orbit ( $v=v_{\text{av}}=\frac{2\pi r_{\text{av}}}{T}$ ), we conclude with the following formula for the angular precession frequency:

${\omega }_{\text{p}}=\frac{2 \pi GM}{c^2{r}_{\text{av}}T}$ (15)

and the formula for the advance of the perihelion (measured as the advance angle per revolution):

$\Delta \phi ={\omega }_{\text{p}}T=\frac{2\pi GM}{c^2{r}_{\text{av}}}$ (16)

Following the assumption on an average radius of r_av to be equal $\begin{array}{l}a\left(1-e^2\right)\\ a\left(1-e^2\right)\end{array}$ , where a is the major half-axis of the ellipse with eccentricity e, the formula is identical to the known Einstein formula (resulting from considerations of general relativity theory), up to factor 3 in the numerator (in Einstein’s formula we find 6π in the numerator) [6-12]. A quantity $a\left(1-e^2\right)$ is called a semi-latus rectum, and for Mercury we have: e = 0.206 and a = 0.579 · 10¹¹ m [23], which gives the advance of the perihelion resulting from general relativity a famous $△{\phi }_{\text{GR}}\approx 0.104"$ per revolution (it is about 43" per century), confirmed up to a high precision by recent results [24]. For simplicity of assumptions (point masses, circular orbits) and simplicity of calculations, the result is quite satisfactory.

Precession of electron in hydrogen atom·

We assume for a ground state: orbit’s radius r₁ = 0.53 · 10^-10 m, v1 = 2.2 · 10⁶ m/s. The force of an interaction between an electron and a proton is then (assuming a circular orbit):

$F_1=e^2/(4\pi {\epsilon }_0 r_1{}^2)=8.2\cdot {10}^{-8}\text{ N }$ (17)

And the angular precession frequency:

${\omega }_1=\frac{v_1{F}_1}{m_{\text{el}}{c}^2}=2.2\cdot {10}^{12}\text{ 1}/\text{s}$ (18)

Note that the angular frequency of the electron's own rotation in the first orbit (according to Bohr’s model) is ω₀ = 4.15·10¹⁶ 1/s, which gives a ratio ω₁/ω₀ ≈ 0.53 · 10-4. This ratio for Earth is 4 orders of magnitude smaller and equals ~10^-8.

The calculations presented are based on the dynamics equation (1), which is valid both in the four-dimensional theory of special relativity and in the alternative theory based on the classical equation for systems with variable mass in 3D, supplemented with a linear relationship between mass and energy. The independence of the dynamic equation (1) from the assumptions of the adopted model increases its rank and increases its importance for the description of reality. All subsequent calculations are a consequence of simple transformations in real space.

This paper presents a derivation of the formula for the frequency of orbital angular precession in the field of central forces. The point-mass assumption was made, which significantly simplifies the calculations and narrows the problem down to purely relativistic effects. Classical components, such as deviation from the sphericity of the object (quadrupole moment, leading also to the nutation phenomenon), or the influence of moments of forces resulting from interactions with neighboring objects (perturbations), were omitted.

Based on the division of each external force into two components (F_r and F_p) it is easy to show that the force component F_r is a modified external force with a relativistic factor γ-2. The dependence of the relativistic component F_r on velocity causes the precession of the shape of the classical orbit, but the orbit for the central force remains in one plane because the moment of the central force is equal to zero. Experimental observation leads to perihelion precession in plane motion around the Sun.

In turn, the F_p component, although it does not affect the energy change, has a direct influence on the precession phenomenon. The most spectacular action of this force is the appearance of a rotating magnetic field around a current-carrying conductor, as shown in our previous works. Another example is the relativistic precession of the velocity and orbit.

Relativistic precession is small for gravity fields and usually disappears in the classical corrections related to the asymmetry of the object (e.g., nutation) or the disturbance of the centrality of the interaction, including by other neighboring objects. For Earth, the period of purely relativistic precession goes back millions of years and is very difficult to observe against the background of much faster classical precession. The proportion of relativistic precession to the frequency of natural turns is in the order of 10^-8 and its influence on the rotation is very small. It looks better for Mercury, where the value of the relativistic correction for the point mass is 3 times lower than that resulting from the general relativity theorem. Our analytical results are in line with many other attempts made “outside” the general relativity.

Much shorter precession times are observed for an electron in a hydrogen atom. Here, the precession period is at the level of 10^-12 s, which may have a significant impact on the formation of spatial orbitals. The ratio of the precession frequency to the natural rotation frequency is on the order of 10^-4 and is 4 orders of magnitude higher than in the case of the planetary system. Hence, there is a difference in the motion of the planets with respect to the motion of the electrons in the atom. While for the planets (due to the long period of rotation in the orbit) it is only a small correction and the movements of the planets are basically flat, for the electrons it becomes the dominant effect, and the relativistic correction essentially corrects the movement of the electron. Thus, the relativistic corrections for atoms fundamentally modify the description of the motion of microscopic objects.

We believe that the results of our work can show how observations known from special and general relativity can be concluded from classical mechanics with fair justification and accuracy. The orbit’s precession, for which the precession component of the external field is responsible based on our studies, in general relativity is obtained by including a velocity-depending potential term in the Lagrangian. In our classical-mechanical studies, the reasoning is similar. This brings us to the conclusion that the formulas we obtained and the concepts behind them can also contribute to the understanding of relativistic phenomena based on classical mechanics. In future applications of our methodology, we can consider the coherent picture of electromagnetism, Lorentz transformations of the electric and magnetic fields, or perhaps even the quantum-mechanical behavior of electrons in atoms.

The authors kindly acknowledge the fruitful discussion with A. Bzdak and thank you for the words of support. Financial support from AGH University of Krakow with research subvention to the Faculty of Physics and Applied Computer Science under grant no. 16.16.220.842 is acknowledged.

Data availability

The data used to support the findings of this study are available from the corresponding author upon request.

1. Rindler W. Introduction to Special Relativity. 2nd ed. Clarendon Press; 1991. Available from: https://philpapers.org/rec/RINITS
2. Wolny J, Strzałka R. Momentum in the dynamics of variable-mass systems: classical and relativistic case. Acta Phys Pol A. 2019;135:475-479. Available from: https://doi.org/10.12693/APhysPolA.135.475
3. Wolny J, Strzałka R. Description of the motion of objects with sub- and superluminal speeds. Am J Phys Appl. 2020;8:25-28. Available from: http://dx.doi.org/10.11648/j.ajpa.20200802.12
4. Wolny J, Strzałka R. Relativistic equation of motion in the presence of a moving force field. Novel Res Sci. 2021;6:1-5.
5. Cester F, Clemente M, Korf H-M. Newton and Relativity: An alternative approach to relativistic mechanics by means of the Lex Secunda. Book on Demand; 2021.
6. Einstein A. The foundation of the general theory of relativity. Ann Phys. 1916;49:769-822. Available from: http://dx.doi.org/10.1002/andp.19163540702
7. Fitzpatrick R. An Introduction to Celestial Mechanics. Cambridge University Press; 2012. Available from: https://doi.org/10.1017/CBO9781139152310
8. Brown K. Reflections on Relativity. Independently published.
9. Kerner R, Van Holten JW, Colistete R Jr. On the quantum nature of the classical limit. Class Quant Grav. 2001;18:4725-4742. Available from: https://iopscience.iop.org/article/10.1088/0264-9381/18/22/302/meta
10. Arnold VI. Mathematical Methods of Classical Mechanics. Springer Verlag; 1978. Available from: https://link.springer.com/book/10.1007/978-1-4757-1693-1
11. Abramowicz MA, Kluzniak W. The origin of the deflection of light by the sun's gravitational field. Gen Rel Grav. 2003;35:69-77. Available from: https://link.springer.com/article/10.1023/A:1021354928292
12. Weinberg S. Gravitation and Cosmology. New York: John Wiley and Sons; 1972.
13. Dyson FW, Eddington AS, Davidson CR. A determination of the deflection of light by the sun's gravitational field, from observations made at the solar eclipse of May 29, 1919. Philos Trans R Soc A. 1920;220:291-333. Available from: https://doi.org/10.1098/rsta.1920.0009
14. Phipps TE Jr. Mercury’s precession according to special relativity. Am J Phys. 1986;54:245-247. Available from: https://www.scirp.org/reference/referencespapers?referenceid=762195
15. Biswas T. Minimally relativistic Newtonian gravity. Am J Phys. 1988;56:1032-1036. Available from: https://doi.org/10.1119/1.15385
16. Frisch DH. Simple aspects of post-Newtonian gravitation. Am J Phys. 1990;58:332-337. Available from: https://doi.org/10.1119/1.16165
17. Jefimenko OD. Gravitation and Cogravitation. Star City: Electret Scientific Company; 2006.
18. de Matos CJ, Tajmar M. Advance of Mercury perihelion explained by cogravity. Available from: https://arxiv.org/ftp/gr-qc/papers/0304/0304104.pdf
19. Wayne R. Explanation of the perihelion motion of Mercury in terms of a velocity-dependent correction to Newton’s law of gravitation. Afr Rev Phys. 2015;10:26. Available from: http://lamp.ictp.it/index.php/aphysrev/article/viewArticle/1074
20. Lemmon TJ, Mondragon AR. Kepler’s orbits and special relativity in introductory classical mechanics. Available from: https://doi.org/10.48550/arXiv.1012.5438
21. Hansen D, Hartong J, Obers NA. Action principle for Newtonian gravity. Phys Rev Lett. 2019;122:061106. Available from: https://doi.org/10.1103/PhysRevLett.122.061106
22. Corda C. The secret of planets’ perihelion between Newton and Einstein. Phys Dark Universe. 2021;32:100834. Available from: https://doi.org/10.1016/j.dark.2021.100834
23. Williams DR. Mercury fact sheet. 2024. Available from: http://nssdc.gsfc.nasa.gov/planetary/factsheet/mercuryfact.html
24. Park RS, Folkner WM, Konopliv AS, Williams JG, Smith DE, Zuber MT. Precession of Mercury's perihelion from ranging to the MESSENGER spacecraft. Astron J. 2017;153:121-128. Available from: https://iopscience.iop.org/article/10.3847/1538-3881/aa5be2/meta