String Theory without Extra Dimensions and Without Supersymmetry

We know that until today no experiment observation has shown the existence of Supersymmetric particles [1] or additional dimensions.

Despite the installation of the large particle accelerator (LHC) since 2007 [2]. So to overcome this major problem it is necessary to think of a new version of the string theory without extra dimensions and without supersymmetric particles.

For this, I propose the following axiomatic system:

Axiom 1:

∀xϵIR we have: $-\text{xIx}=\text{x?}$ and we read −x Integration of x equal to x intermediate.

Axiom 2:

∀xϵIR we have: $-xIx=xI-x=x ?$

Axiom 3:

∀xϵIR we have: xIx = x

Nomenclature:

We call H the set of intermediate numbers.

Algebraic structure:

Let H be a group endowed with the law of addition

(H; +) and $\left(x?;y?\right)\in H^2$ we have:

$x?+y?=-xIx+-yIy=\{\begin{array}{c}-x+-yIx+y\\ or\\ -x+yIx+-y\end{array}$

$\{\begin{array}{c}-(x+y)Ix+y\\ or\\ y-xIx-y\end{array} =\{\begin{array}{c}-\left(x+y \right)Ix+y\\ or\\ -(x-y)Ix-y\end{array}$

We pose a = x + y and b = x - y, and we have

$x?+y?=\{\begin{array}{c}-aIa =a?\\ OR\\ -bIb =b?\end{array}$

So the sum of two elements of H is also an element of H.

It follows that the law (+) is a law of internal composition for the group of intermediate numbers.

We now show that the law of addition is associative:

If $\left(x?;y?;z ?\right)\in H^3$ we have:

$x ? +(y?+z?)=-x Ix+(-yIy+-zIz)=$

- x Ix + [-y +-zIy +z OR -y+zIy +- z] =

$-x Ix+\left[-\left(y+z\right)Iy+z OR -\left(y-z\right)Iy-z\right]$

$\{\begin{array}{c}-x+-\left(y+z\right)Ix +y+z=-\left(x +y+z\right)Ix +y+z.\\ OR \\ -x +y+zIx+-\left(y+z\right)=-\left(x -y-z\right)Ix-y-z.\\ OR\\ -x+-\left(y-z\right)Ix+y-z=-\left(x+y-z\right)Ix+y-z.\\ OR\\ -x+y-zIx+-\left(y-z\right)=-\left(x-y+z\right)Ix-y+z.\end{array}$

Also, we have:

(x?+y?)+z?=(-xIx+-yIy)+-zIz=

[-x+-yIx+y OR-x+yIx+-y] +-zIz=

[-(x+y)Ix+yOR-(x-y)Ix-y]+-zIz=

[-(x+y)Ix+yOR -(x-y)Ix-y]+-zIz=

$\{\begin{array}{c}-\left(x+y\right)+-zIx+z=-\left(x+y+z\right)Ix+y+z\\ OR\\ -\left(x+y\right)+zIx+y+-z=-\left(x+y-z\right)Ix+y-z\\ OR\\ -\left(x-y\right)+-zIx-y+z=-\left(x-y+z\right)Ix-y+z.\\ OR\\ -(x-y)+zIx-y+-z=-\left(x-y-z\right)Ix-y-z\end{array}$

By comparing the two results above we conclude that they are equal.

=> $\forall \left(x?;y?;z?\right)\in H^{3 }$ we have,

$x?+\left(y?+Z?\right)=\left(x?+y?\right)+z?$

=> the addition law is associative in H.

Let’s now prove that zero is an intermediate number:

We know that zero is a neutral number: (-0 = + 0 = 0).

Besides, intermediate numbers are also neutral numbers because they are neither negative nor positive numbers

According to Axiom 1:

$\forall x\in IR$ we have $-\text{xIx}=x?\Rightarrow x?$ Has no Sign. $\Rightarrow So O\in H.$

Checking for now, that zero is the neutral element for the internal composition law (+) in H:

Let $x ?\in H$ we have,

$x?+0=-xIx+0I0 \left[because:\forall x\in IR we have xIx=x\left(axiom number 3\right)\right]$ =>

$x?+0=-xIx+0I0=-x+0Ix+0=-xIx=x?$

=> So zero is the neutral element for the group (H; +).

Does there now exist a symmetric element for the number x ? in the group (H; +):

If $x ?\in H$ we have:

$x?+x?=\{\begin{array}{c}-xIx+-xIx=-x+-xIx+x\\ OR\\ -xIx+xI-x=-x+xIx+-x\end{array}$

So $x?+x?=\{\begin{array}{c}-2xI2x=2x?\\ or\\ 0I0=0\end{array}$

It follows that each number of the group (H; +) is the inverse of itself: any element of H admits a Symmetric element for the law (+) which is itself.

Let’s prove finely that the law of addition is commutative in H:

If $(x?;y?)\in H^2$ we have:

$\text{x }?+\text{y}?=\{\begin{array}{c}-xIx+ -yIy=-x+-yIx+y\\ OR\\ -xIx+yI-y=-x+yIx+-y\\ OR\\ xI-x+-yIy=x+-yI-x+y\\ OR\\ xI-x+yI-y=x+yI-x+-y\end{array}$

$x?+y?=\{\begin{array}{c}-\left(x+y\right)Ix+y\\ OR\\ -\left(x-y\right)Ix-y\\ OR\\ x-yIy-x\\ OR\\ x+yI-(x+y)\end{array}$

As far as we have:

$\text{y}?+\text{x}?=\{\begin{array}{c}-yIy+-xIx=-y+-xIy+x\\ OR\\ -yIy+xI-x=-y+xIy+-x\\ OR\\ yI-y+-xIx=y+-xI-y+x\\ OR\\ yI-y+xI-x=y+xI-y+-x\end{array}$

$\text{y}?+\text{x}?=\{\begin{array}{c}-\left(y+x\right)Iy+x\\ OR\\ x-yIy-x\\ OR\\ -\left(x-y\right)Ix-y\\ OR\\ y+xI-(y+x)\end{array}$

=> It results after the comparison of the two operations $(x?+y?andy?+x?)$ which are equal. So $\forall \left(x?;y?\right)\in H^2$ we have: $x?+y?=y?+x?$

It can be concluded that the group H endowed with the law (+) is an abelian or commutative group.

Axiom 4:

Consider that $\underset{\text{v}}{\to }$ is a Vector in the vector Space, so we have:

$\underset{\text{v}}{\leftrightarrow }=-\underset{\text{v}}{\to } I\underset{\text{v}}{\to }$ and we read: V intermediate equals a $-\underset{V}{\to }$ integration of $\underset{V}{\to }$ .

Corollary n°1:

V intermediate has the direction of v and -v at the same time.

Corollary n° 2:

$\parallel \underset{\text{v}}{\leftrightarrow }\parallel =\parallel -\underset{\text{v}}{\to }\parallel I\parallel \underset{\text{v}}{\to }\parallel$ . But we know that the norm is always positive. So we have:

$\parallel \underset{\text{v}}{\leftrightarrow }\parallel =\parallel -\underset{\text{v}}{\to }\parallel I\parallel \underset{\text{v}}{\to }\parallel =\parallel \underset{\text{v}}{\to }\parallel$ [because (axiom number 3)].

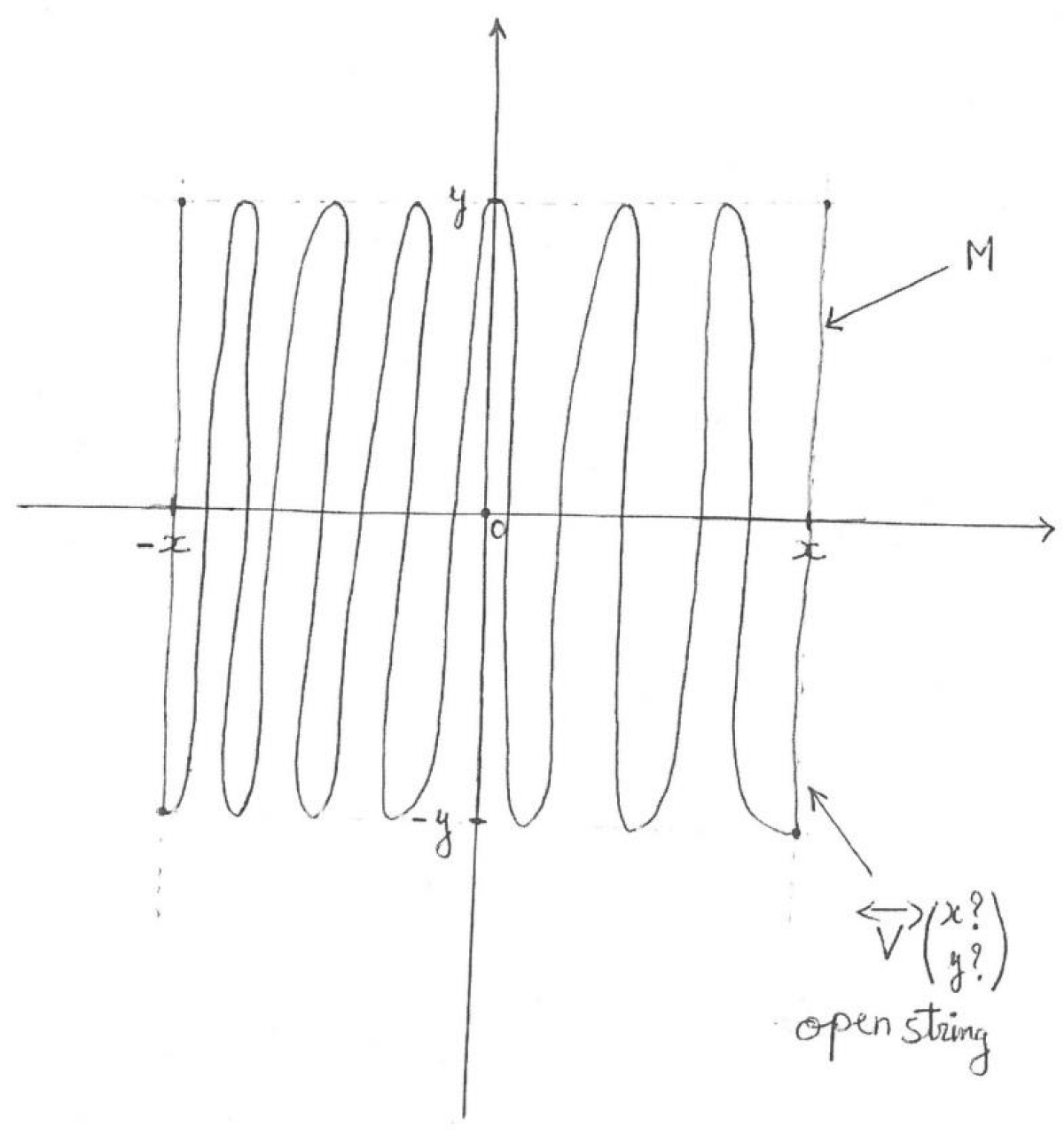
Graphic illustration: Consider that M is a point of the Euclidean plane with M of coordinates $(x?;y?)=\text{ >}$

So we have the following diagram (Figure 1).

The conclusion is that M is delocalized on the Euclidean plane. Indeed M is identified with an intermediate vector of the same coordinates (x ?; y ?).

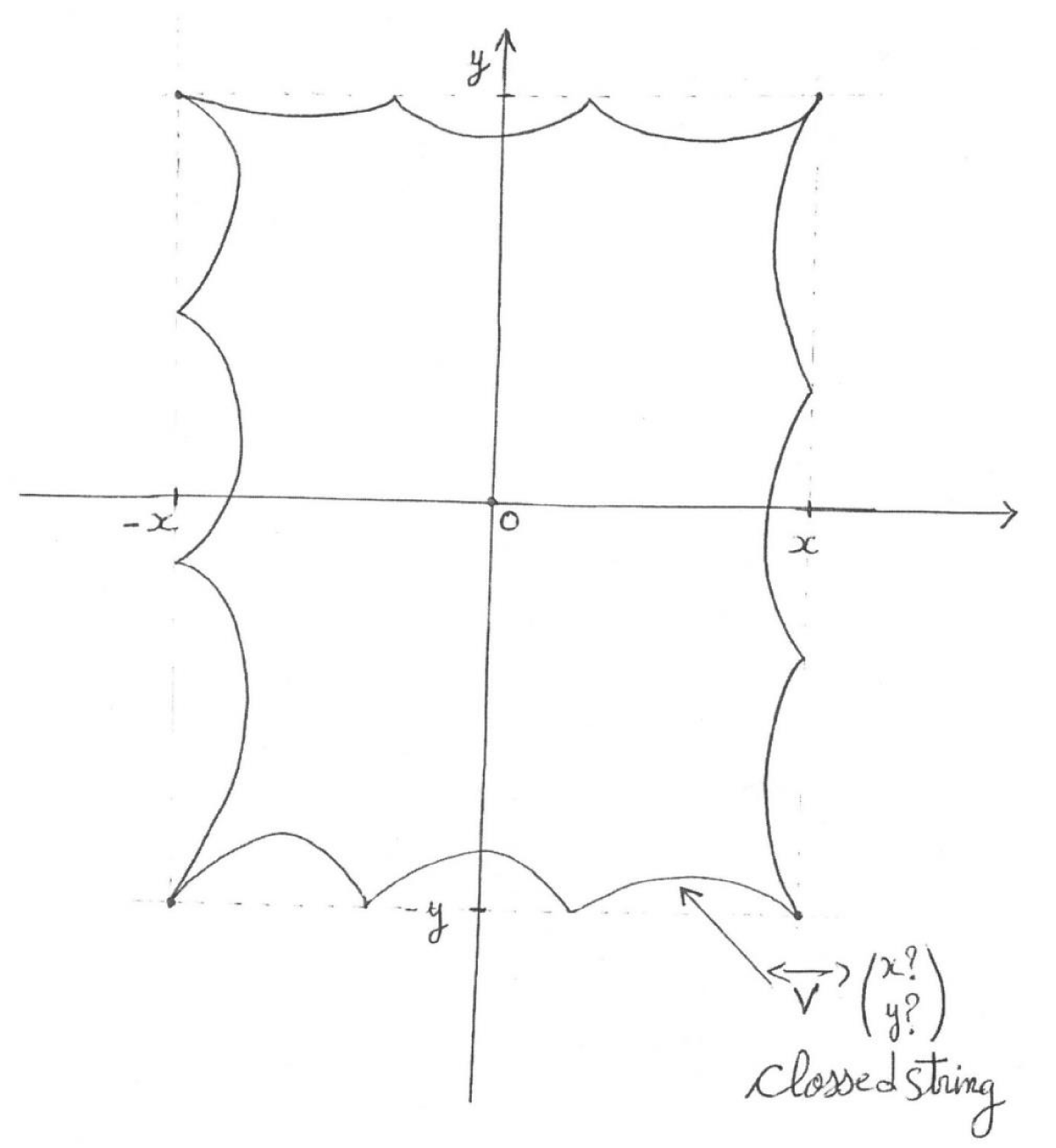
Remark:

$\underset{\text{v}}{\leftrightarrow }$ has a dynamic structure (it can vibrate ) and it can be an open intermediate vector (Figure 1), or a closed intermediate Vector (Figure 2).

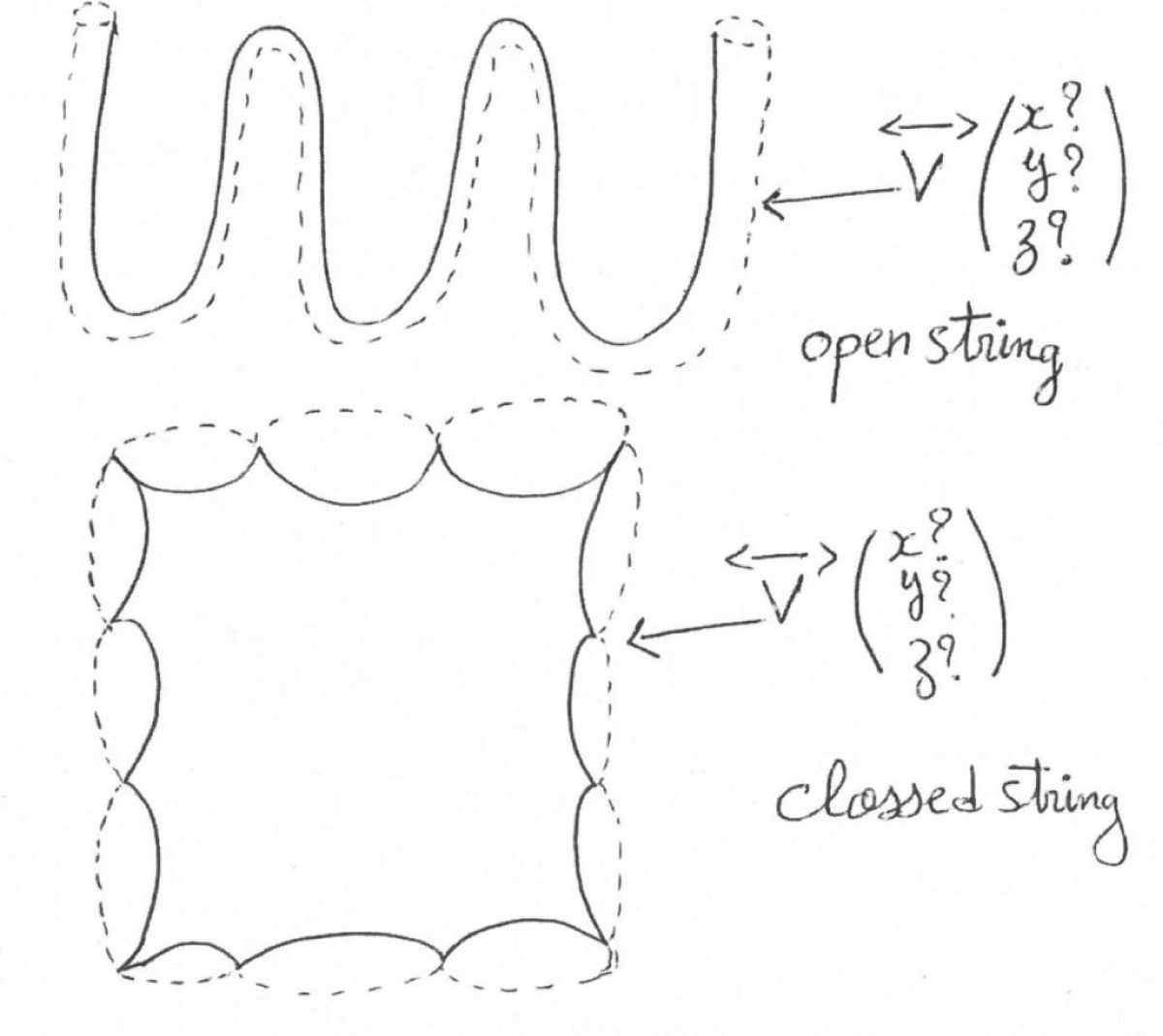
Corollary:

In space, the intermediate vectors have a volume, and we have the following diagram (Figure 3).

The nature of the intermediate vectors Space (S?):

Consider that $\left(\underset{\text{v}}{\leftrightarrow };\underset{u}{\leftrightarrow }\right)\in S{?}^2$ , with $\underset{\text{v}}{\leftrightarrow }\left(\begin{array}{c}x?\\ y?\\ z?\end{array}\right)$ and $\underset{u}{\leftrightarrow }\left(\begin{array}{c}a?\\ b?\\ c?\end{array}\right)$ . So we have:

$\underset{\text{v}}{\leftrightarrow }+\underset{u}{\leftrightarrow } = \left(\begin{array}{c}x?\\ y?\\ z?\end{array}\right)+\left(\begin{array}{c}a?\\ b?\\ c?\end{array}\right)=\{\begin{array}{c}-xIx+-aIa\\ -yIy+-bIb\\ -zIz+-cIc\end{array}=>$

$\underset{\text{v}}{\leftrightarrow }+\underset{u}{\leftrightarrow }= \{\begin{array}{c}-x+-aIx+a OR-x+aIx+-a\\ -y+-bIy+b OR -y+bIy+-b\\ -z+-cIz+c OR -y+cIz+-c\end{array}=>$

$\underset{\text{v}}{\leftrightarrow }+\underset{u}{\leftrightarrow }=\{\begin{array}{c}-\left(x+a\right)Ix+aϵH\\ -\left(y+b\right)Iy+bϵH OR\\ -\left(z+c\right)Iz+cϵH\end{array}\{\begin{array}{c}-\left(x-a\right)Ix-aϵH\\ -\left(y-b\right)Iy-bϵH\\ -\left(z-c\right)Iz-cϵH\end{array}$

$\underset{\text{v}}{\leftrightarrow }+\underset{u}{\leftrightarrow }=\{\begin{array}{c}-\left(x+a\right)Ix+aϵH\\ -\left(y+b\right)Iy+bϵH\\ -\left(z+c\right)Iz+cϵH\end{array}OR\{\begin{array}{c}-\left(x-a\right)Ix-aϵH\\ -\left(y-b\right)Iy-bϵH\\ -\left(z-c\right)Iz-cϵH\end{array}$

=> So the sum of two intermediate vectors is an intermediate vector: the addition law is an internal composition law for S.

Either now: $\underset{\text{v}}{\leftrightarrow }\in S?$ and $k\in IR$ , we have:

$k.\underset{\text{v}}{\leftrightarrow } =k.\left(\begin{array}{c}x?\\ y?\\ z?\end{array}\right)=k.\left(\begin{array}{c}-xIx\\ -yIy\\ -zIZ\end{array}\right)\text{ OR }k.\left(\begin{array}{c}xI-x\\ yI-y\\ zI-Z\end{array}\right)=>$

$k.\underset{\text{v}}{\leftrightarrow }=\left(\begin{array}{c}-kxIkx\in H\#\\ -kyIky\in H\#\\ -kzIkz\in H\#\end{array}\right)\text{OR }\left(\begin{array}{c}kxI-kx\in H\#\\ kyI-ky\in H\#\\ kzI-kz\in H \#\end{array}\right)=>$

So $\forall k\in IR$ and $\underset{\text{v}}{\leftrightarrow }\in S?$ we have:

$k.\underset{\text{v}}{\leftrightarrow }\in S?$ => the Set S? endowed with the two laws (+ ; .) is a Vector Space.

String theory and the problem of interpreting Young’s double slit experiment:

We know from quantum mechanics that any quantum object is neither a particle nor a wave. So how to explain the interference figures that appear in Young’s experiment despite being typical of waves? Thus, to overcome this problem it is necessary to consider that each quantum object is an intermediate vector that carries in itself a quantity of energy discrete and well defined by Planck’s equation: E = h.v [3].

So when the photons are emitted by the source there are some of them which arrive at the plate pierced in two holes in phase.

And their sum will be doubled and we obtain bright spots on the screen.

On the other hand, if the photons arrive in phase opposition then their sum will be zero and we obtain dark spots on the screen.

Mathematical demonstration:

If y1 and y2 are two photons we know that a photon is an intermediate vector. So we have:

$\underset{y₁}{\leftrightarrow } +\underset{y₂}{\leftrightarrow } =\underset{\text{v}}{\leftrightarrow }+\underset{\text{v}}{\leftrightarrow }=-\underset{\text{v}}{\to }I\underset{\text{v}}{\to }+-\underset{\text{v}}{\to }I\underset{\text{v}}{\to }$ =>

$\underset{y₁}{\leftrightarrow } +\underset{y₂}{\leftrightarrow } =\{\begin{array}{c}-\underset{\text{v}}{\to }+-\underset{\text{v}}{\to }I\underset{\text{v}}{\to }+\underset{\text{v}}{\to }=-2\underset{\text{v}}{\to }I2\underset{\text{v}}{\to }\\ OR \\ -\underset{\text{v}}{\to }+\underset{\text{v}}{\to }I\underset{\text{v}}{\to }+-\underset{\text{v}}{\to }=\underset{0}{\to }I\underset{0}{\to }\end{array}$ =>

$\underset{y₁}{\leftrightarrow } +\underset{y₂}{\leftrightarrow }=\{\begin{array}{c}2\underset{\text{v}}{\leftrightarrow } bright spots.\\ OR\\ \underset{0}{\to }dark spots\end{array}$

The conclusions are that the sum of two quantum objects of the same species can be constructive

( $\underset{\text{v}}{\leftrightarrow }+\underset{\text{v}}{\leftrightarrow }=2\underset{\text{v}}{\leftrightarrow }$ , with a probability of occurrence equal to $\frac{1}{2}$ ). But it can be destructive ( $\underset{\text{v}}{\leftrightarrow }+\underset{\text{v}}{\leftrightarrow }=\underset{0}{\to }$ , with a probability of occurrence equal to $\frac{1}{2}$ ).

On the other hand, Young’s experiment reveals to us that if we put a detector to allow us to know through which slit the quantum object has entered, then the phenomenon of interference disappears. Why?

Because the measurement operation affects the very nature of the quantum object, that is to say, it upsets its physical identity, namely it ceases to be an intermediate vector. This transformation of physical identity is mathematically permitted:

If $\underset{\text{v}}{\leftrightarrow }$ and $\underset{u}{\leftrightarrow }$ two intermediate vectors of the intermediate space S? with $\underset{\text{v}}{\leftrightarrow }\left(\begin{array}{c}x?\\ \begin{array}{c}y?\\ z?\end{array}\end{array}\right)$

and $\underset{u}{\leftrightarrow }\left(\begin{array}{c}a?\\ b?\\ c?\end{array}\right)$ . We have:

$\underset{\text{v}}{\leftrightarrow }.\underset{u}{\leftrightarrow }=\left|\begin{array}{c}x?\times a?\\ y?\times b?\\ z?\times c?\end{array}\right|=\left|\begin{array}{c}-xIx\times -aIa\\ -yIy\times -bIb\\ -zIz\times -cIc\end{array}\right|$ =>

$\underset{\text{v}}{\leftrightarrow }.\underset{u}{\leftrightarrow }=\left|\begin{array}{c}-x\times -aIx\times a OR-x\times aIx\times -a\\ -y\times -bIy\times b OR-y\times bIy\times -b\\ -z\times -cIz\times c OR-z\times cIz\times -c\end{array}\right|$

$\underset{\text{v}}{\leftrightarrow }.\underset{u}{\leftrightarrow }=\left|\begin{array}{c}axIax OR -axI-ax\\ ybIyb OR -ybI-yb\\ zcIzc OR -zcI-zc\end{array}\right|$

$\underset{\text{v}}{\leftrightarrow }.\underset{u}{\leftrightarrow }=\left|\begin{array}{c}ax OR -ax\\ yb OR -yb\\ zc Or -zc\end{array}\right|$ ; According to axiom number 3

So, $\underset{\text{v}}{\leftrightarrow }\underset{u}{\leftrightarrow } =\left|\begin{array}{c}ax\notin H \#OR -ax\notin H\#\\ yb\notin H \#OR -yb \notin H\#\\ zc\notin H \#OR -zc\notin H\#\end{array}\right|$ =>

$\underset{\text{v}}{\leftrightarrow }.\underset{u}{\leftrightarrow }$ is not an intermediate vector.

Thus, the effect of the experimental measurement has upset the physical nature of the quantum object and we will have more interference phenomena on the screen.

String theory and the problem of dark energy:

We know since Galileo that the universe is a physical object; it is the physical system that includes all other physical systems. In addition, this physical object has a dynamic geometric structure according to general relativity.

Thus, can we content ourselves with admitting that the large structures of the universe such as the galaxies and the clusters of galaxies evolve and act with an abstract geometric structure of the universe, that is to say, a space-time that does not have not in itself a proper physical structure?

In reality, if the universe is a physical object then by definition its geometric structure has its own material structure. Moreover, if we admit that quantum reality is the fundamental physical reality from which the macroscopic physical world emanates, then the geometric structure of the universe has a quantified structure that has evolved over time and since the singularity of the Big Bang.

And since we have postulated that any quantum object is an intermediate vector then the geometric structure of the universe is constituted by intermediate.

Vectors of discrete and well-defined energy: these are the space-time quanta which is expressed by the following intermediate vector:

$\underset{q}{\leftrightarrow }=-\underset{h\text{v}}{\to }I\underset{h\text{v}}{\to }=\underset{h\text{v}}{\leftrightarrow }$ =>

$\underset{h\text{v}}{\leftrightarrow }$ : is the fundamental volume of space – time.

In addition, we know that quantum reality is a chaotic and random reality. So, similarly, the geometric structure of the universe at the quantum level is in a chaotic state and it will be endowed with its own entropy.

Based on the second principle of thermodynamics, we conclude that the entropy (S) of the geometric structure of the universe can only increase over time. Thus the geometric structure of the universe obeys the following Law:

${\displaystyle \sum }_{n=1}^{\infty }n.\underset{h\text{v}}{\leftrightarrow }=K_B L{n}_{(\Omega )}$ ; with

$n\in IN$ and $K_B L{n}_{(\Omega )}=S$ is the Boltzmann entropy equation.

In conclusion, the acceleration of the expansion of the universe is due to the growth of the entropy of the geometric structure of space-time. Thus dark energy [4] is a physical property of the universe: a quantified and chaotic structure that generates the dilation of the cosmos.

String theory and the dark matter problem:

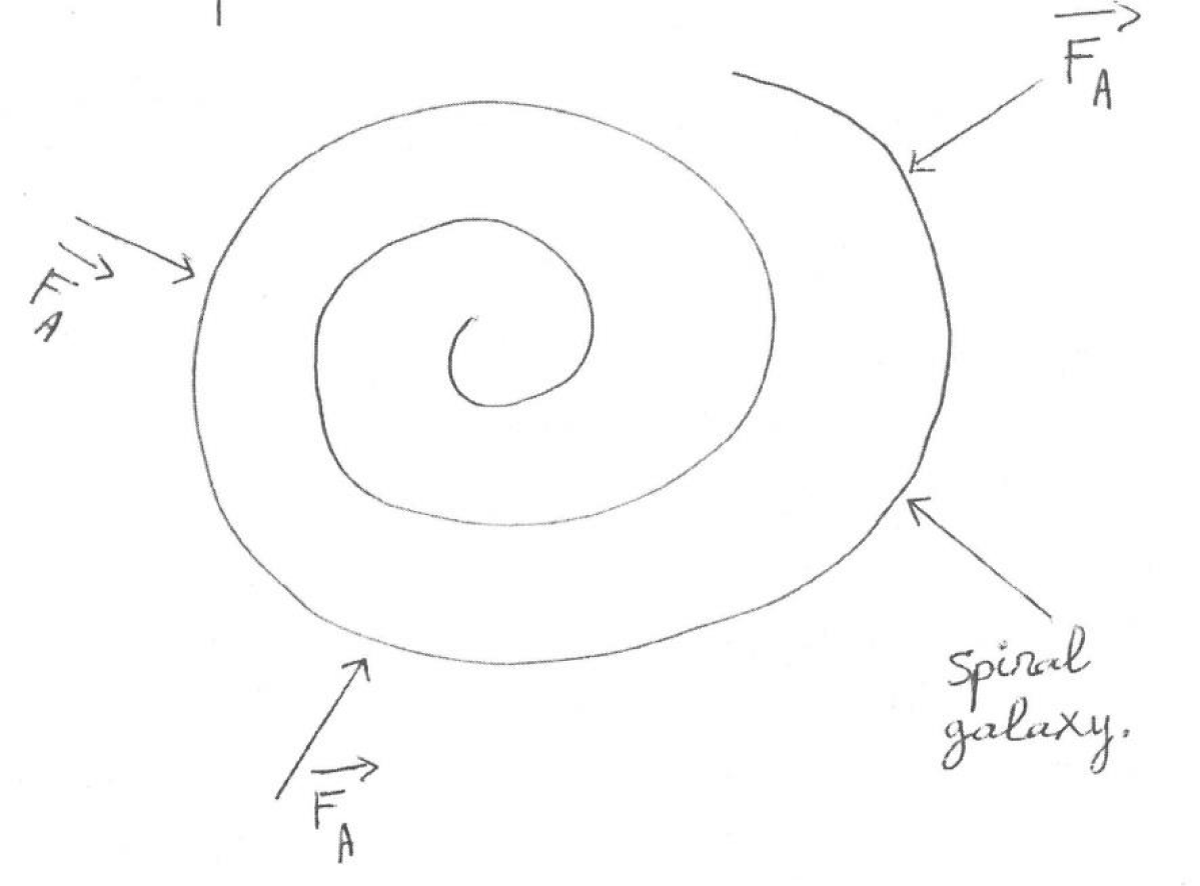
Since galaxies and clusters of galaxies evolve within a quantified and chaotic geometric structure then they experience the effect of this substantial structure of space-time. And instead of advancing the thesis of the existence of a non–baryonic matter to explain the rotation curves of Vera Rubin [5], it is natural to consider that the geometric structure of Space–time acts on the great structures of the cosmos, as the latter act on the geometry of the universe by bending the space-time: It’s a reciprocal interaction.

So the geometric structure of space-time exerts a force of action on galaxies and clusters of galaxies which suggests that there is a kind of halo of exotic matter that surrounds the external structure of these. A graphic illustration is shown in Figure 4.