Chaos to Cosmos: Quantum Whispers and the Cosmic Genesis

Quantum fluctuations, usually arising from the inherent uncertainty in the quantum fields, are pivotal in understanding the universe at both the small and large scales. Even though fluctuations are usually unobservable and rather small, they give significant observable effects during specific epochs under specific conditions. During the early epochs of the universe, the fluctuations were scaled, resulting in the primordial density perturbations that gave rise to the large-scale structure of the universe and the observed inhomogenities. In this paper, we study the basic origin, structure, evolution, and imprints of fluctuations during the inflationary period resulting in large-scale structure formation. We use the Mukhanov-sasaki formalism to model scalar perturbations, embedding the theoretical results into observations. Theoretical predictions show an almost scale-invariant power spectrum with stringent constraints on the inflationary parameters. It further states that in the very early universe, the inflatons that are quanta of the primordial field were highly filled in the degenerate quantum state. This carries large potential energy that results in an exponential expansion of the universe. During post post-inflationary period the inflaton dominated the Universe’s energy density; they interact among themselves and due to non-linear effects, these inhomogeneities grow which amalgamate into spatially distinguishable patches in our observable universe. Our understanding projects us towards the fact that fluctuations play a pivotal role in understanding the structure formation at micro, macro, and far-macro scales. This study also addresses the significance of quantum fluctuations in cosmic evolution and manifests the enduring relevance in addressing some of the profound mysteries of our universe.

Quantum fluctuations are one of the most profound and fundamental consequences in quantum physics and stand as a pillar in understanding the behavior in the smallest and largest parts of the universe. They arise from the fundamental uncertainties that are encoded in the principles of quantum mechanics, such as Heisenberg’s uncertainty principle, according to which it is impossible to measure or know certain pairs of physical properties, such as position and momentum or energy and time, with arbitrary precision simultaneously. This inherent ”fuzziness” of the quantum world gives rise to temporary and spontaneous changes in the energy or state of a system, even in what we perceive as space [1-7]. At the heart of quantum fluctuations lies the concept of the quantum vacuum, a state that is far from being truly ”empty.” Unlike the classical notion of a vacuum as a complete void, the quantum vacuum is a dynamic sea of virtual particles constantly appearing and annihilating, a direct consequence of quantum field theory.

These ripples take the form of temporary violations of classical energy conservation, allowed by the uncertainty principle, and play a critical role in determining the nature of reality. These are not just abstract ideas but have profound physical consequences, from the forces between particles to the structure of spacetime itself. Quantum fluctuations are at the heart of many of the most important phenomena in physics [5]. For example, they provide the underlying mechanism for the Casimir effect. In cosmology, quantum fluctuations during the inflationary epoch of the early universe were stretched to macroscopic scales, seeding the formation of large-scale structures such as galaxies and galactic clusters [8]. They are responsible for Hawking radiation in black hole physics, wherein the particle-antiparticle pairs created near the event horizon result in the emission of radiation. The above examples indicate that quantum fluctuations are quite universal across vast domains of physics. Quantum fluctuations form a subject of study bridging across quantum field theory, general relativity, thermodynamics, and condensed matter physics.

They come forth as quantum field theory perturbations around the vacuum state, the fluctuations are always probabilistic; the correlation functions quantify the statistical relationships between the values of fields at different space-time points [9,10]. This statistical treatment predicts measurable effects but also offers insights into the interplay between quantum mechanics and classical phenomena. Cosmologically, quantum fluctuations are responsible for the very fabric of the observable universe.

Quantum fluctuations in the scalar field driving inflation during the inflationary phase of the early universe were amplified and stretched to astronomical scales. These fluctuations, frozen as density perturbations, eventually led to the formation of galaxies and other cosmic structures observed today. The anisotropies in the Cosmic Microwave Background (CMB) [2], the relic radiation from the Big Bang, are direct imprints of these primordial quantum fluctuations, providing one of the most compelling pieces of evidence for their existence. They are integral to our current understanding of vacuum stability and the spontaneous symmetry breaking that controls fundamental forces and particle behavior. Despite their pervasive influence, quantum fluctuations remain a deeply enigmatic and profoundly intriguing topic in theoretical physics. They challenge classical intuitions about the nature of energy, space, and time, and force us to rethink fundamental concepts like causality and locality. Experimental evidence, such as the precise measurements of the Casimir force, the detection of vacuum polarization effects, and the observations of the CMB anisotropies, have confirmed their theoretical predictions to remarkable accuracy, solidifying their status as a cornerstone of modern physics. As we continue to probe the quantum realm, quantum fluctuations remain at the frontier of many unresolved questions.

We will be particularly studying the theoretical foundation, mathematical descriptions, and the physical iM_plications of quantum fluctuations that play a key role in large-scale structure formation.

The large-scale aggregation of matter in the universe, known as gravitational clustering, originates from primordial quantum fluctuations during inflation [11]. These quantum fluctuations become seeds for density perturbations, which later evolve under gravity to form cosmic structures such as galaxies, clusters, and the large-scale cosmic web. A robust theoretical approach to describe these phenomena is the Mukhanov-Sasaki formalism [2,3], which connects quantum field fluctuations during inflation to the curvature perturbations that later drive gravitational clustering through power spectrum P(k) and two-point correlation function ξ(r).

2.1 Quantum origins of density perturbations

Density perturbations, the seeds for the formation of cosmic structures such as galaxies and galaxy clusters, are seeded by quantum fluctuations of the inflaton field during the inflationary epoch [12]. The rapid expansion of the universe stretches these fluctuations out, turning microscopic quantum phenomena into macroscopic density variations and later into various manifestations of the observable universe.

2.2 The inflaton field

Inflation, a period of exponential expansion in the early universe, is driven by a scalar field called the inflaton field ϕ. The inflaton field’s potential energy dominates during this epoch [13], leading to the accelerated expansion of spacetime. The field ϕ is treated as a quantum field with small perturbations superiM_posed on a homogeneous background [1]

ϕ(x,t) = ϕ0(x,t) + δϕ(x,t) (1)

where ϕ₀ is the spatially homogeneous background field.

δϕ(x,t) represents quantum fluctuations.

The inflaton field and its conjugate momentum obey the celebrated Heisenberg’s Uncertainty principle:

$△\varphi △\pi \varphi \ge \frac{h}{4\pi }$ (2)

This means that the inflaton field cannot be homogeneous; rather, it suffers inevitable quantum fluctuations. These are first confined to sub-horizon scales and therefore behave like the quantum theory dictates.

The evolution of the inflaton field is described by the Klein-Gordon equation in an expanding universe [14]:

$\ddot{\varphi }+3H\dot{\varphi }+\frac{dV}{d\varphi }=0$ (3)

Where, $H=\frac{\dot{a}}{a}$ is the Hubble parameter.

V (ϕ) is an inflation Potential that governs the behavior of the inflation field and the dynamics of inflation.

2.3 Slow-roll approximation

During inflation, the inflaton field evolves slowly due to the dominance of the potential energy V (ϕ) over the kinetic energy ${\dot{\varphi }}^2$ . This is known as the slow-roll approximation, where the following conditions are satisfied:

$\in =\frac{M_P^2}{2}{\left(\frac{\dot{V}(\varphi )}{V(\varphi )}\right)}^2<<1$ (4)

$\eta =M_P^2\left(\frac{\ddot{V}(\varphi )}{V(\varphi )}\right)<<1$ (5)

Where, ϵ is the first slow-roll parameter, controlling the rate of change of the Hubble parameter.

η is the second slow-roll parameter, controlling the curvature of the potential. M_p is the reduced Plank mass.

Under the Slow-Roll approximation the second term dominates over the first term hence the equation of motion is reduced to;

$3H\dot{\varphi }+\frac{dV}{d\varphi }=0$ (6)

This indicates that the field’s motion is primarily driven by the potential, and the acceleration of the field is small [15]. The scale factor a(t) of the universe grows exponentially during inflation. The Hubble parameter H is approximately constant, therefore universe expands exponentially, with the scale factor growing as:

a(t) ∝ e^Ht (7)

The slow-roll approximation is crucial in inflationary models because it allows for an analytic understanding of the inflationary phase. Predictions related to isotropy, homogeneity, and the CMB anisotropies.

2.4 Mukhanov-sasaki formalism

To study the effects of primordial quantum fluctuations regarding the large-scale structure formation we introduce a Mukhanov-Sasaki variable v_k, which describes the quantum perturbations of scalar inflaton field in a gauge-invarant manner, the variable may be defined as;

$v_k=a\left(\delta \varphi +\frac{\dot{\varphi }}{H}\psi \right)$ (8)

Where ψ is a scalar metric perturbation.

The evolution of v_k is governed by the famous Mukhanov-Sasaki equation;

${\ddot{v}}_k+\left(k^2-\frac{\ddot{z}}{z}\right)v_k=0$ (9)

Where,

$z=\frac{a{\dot{\varphi }}_0}{H}$ 1

k is the comoving wavenumber.

2.5 Evolutionary stages

2.5.1 Sub-horizon scale: In this regime (k ≫ aH) where k² dominates and the equation of motion approximates the simple harmonic oscillator as;

¹Dots over z denote derivatives with respect to conformal time.

${\ddot{v}}_k+k^2{v}_k=0$ (10)

These modes oscillate with a frequency proportional to k. The equation has a corresponding oscillatory solution, defining the quantum vacuum fluctuations in Bunch-Davies Vaccum,

v_k ∝ e±ιkη (11)

2.5.2 Super-Horizon scale: In this regime (k ≪ aH) where $\frac{\ddot{z}}{z}$ dominates and the equation of motion is reduced to;

${\ddot{v}}_k-\frac{\ddot{z}}{z}=0$ (12)

In this regime the amplitude of perturbations freezes, thereby preserving the information about perturbations. Hence the perturbations become nearly constant and the solution approximates;

v_k ∝ Constant (13)

2.5.3 Relation between Mukhanov-Sasaki variable and curvature perturbation: The curvature perturbation ζ_k is a gauge-invariant quantity that describes the spatial curvature of comoving hypersurfaces, it becomes constant on super-horizon scales therefore used for tracking the evolution of density perturbations. Hence defined as;

${\zeta }_k=-\psi -H\frac{\delta q}{\rho +P}$ (14)

Where ψ is the curvature perturbation.

ρ and p are the energy density and pressure.

δq is the momentum perturbation.

The statistical properties of v_k directly determine those of ζ_k as the two quantities are related as;

Where,

${\zeta }_k=\frac{v_k}{z}$ (15)

$z=\frac{a{\dot{\varphi }}_{}}{H}$ (16)

${\dot{\varphi }}_0$ is the background inflaton field’s time derivative.

a is the scale factor.

$H=\frac{\dot{a}}{a}$ is the Hubble parameter.

The statistical properties of density perturbations are crucial for understanding the formation of large-scale structures in the Universe. These perturbations, which arise from tiny fluctuations in the distribution of matter and energy in the early Universe, evolve under the influence of gravitational instability, leading to the formation of galaxies, clusters, and larger-scale structures. The concept of Jeans instability describes the conditions under which small density fluctuations in a self-gravitating fluid will grow rather than damp out. This criterion is applied to a gas of particles (or fluid), where gravity competes with other forces (e.g., thermal pressure). The Jeans criterion provides the minimum mass of a perturbation that can collapse under its gravity. If the mass of a region of gas exceeds the Jeans mass, the region will undergo gravitational collapse. For instance, in the early Universe, smaller regions of high density began to collapse into dark matter halos, later attracting baryonic matter to form galaxies and galactic clusters [16].

3.1 Power spectrum and two-point correlation function

The power spectrum is a measure of the distribution of power (or variance) of fluctuations in a field, such as the density contrast, as a function of spatial scale [9]. It is usually used in Fourier space to describe how different spatial scales contribute to the total variance of the field. It is the Fourier transform of the two-point correlation function and gives insight into the distribution of density fluctuations across different wavenumbers k.

In Fourier space, the density contrast δ(x) is written as a sum over modes with wavenumber k

$\delta (x)={\displaystyle \int \frac{d^{3}k}{{(2\pi )}^3}}\delta (k)e^{ikx}$ (17)

The power spectrum P(K) is defined as the average squared amplitude of these Fourier components:

$P(k)=\langle |\delta (k){|}^2\rangle$ (18)

The value of k determines the spatial scale like galaxies, galactic clusters, filaments, and the cosmic-web. The power spectrum and the two-point correlation function are related through the Fourier transform:

$\xi (r)={\displaystyle \int \frac{P(k)}{2{\pi }^2}}\frac{\sin kr}{kr}{k}^{2}dk$ (19)

$P(k)={\displaystyle \int \frac{\sin kr}{kr}\xi (r)r^{2}dr}$ (20)

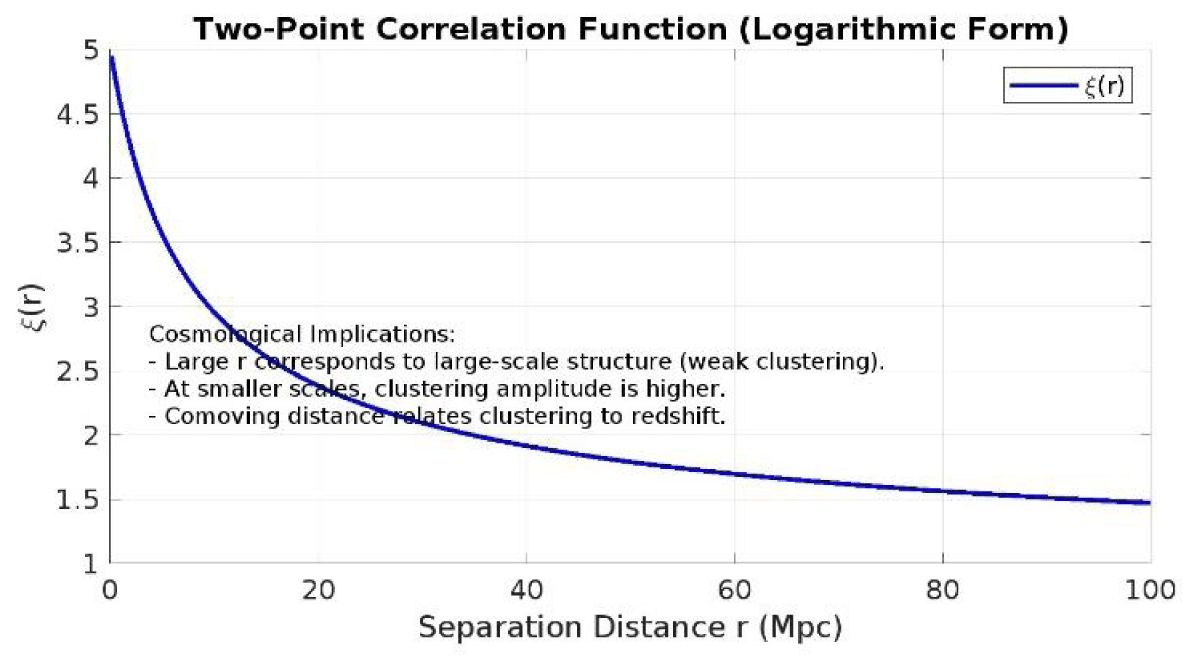
Where ξ(r) is the two-point correlation function that measures the degree of correlation between the density contrasts at two points in space [17]. It quantifies how similar the density is at two different locations separated by a distance r Figure 1.

The two-point correlation function ξ is defined as:

$\xi (r)=\frac{\langle \delta (x)\delta (x+r)\rangle }{\langle {\delta }^2\rangle }$ (21)

The two-point correlation function is often used to describe the clustering of galaxies or dark matter [18]. A higher value of ξ(r) at a given separation r means that there is a greater tendency for matter (or galaxies) to be clustered at that separation. Since the phenomenological logarithmic form is the better fit for the transition from linear to nonlinear clustering regimes, we will be using it as;

$\xi (r)=\frac{A}{1+ln(r/r_0)}$ (22)

Where,

A determines the amplitude of clustering.

r_o is the characteristic scale that determines the transition point.

This form is a phenomenological model used to describe clustering in certain regimes, especially when the correlation weakens gradually over distance. The logarithmic dependence ensures a slower decay compared to a power law or exponential. Thereby logarithmic decay implies a smooth transition from strongly clustered scales to weakly clustered scales [19], making it suitable for intermediate-to-large scale analysis in cosmology as 1;

The power spectrum is easier to compute in Fourier space while the correlation function is easier to visualize in real space [17]. It is sometimes convenient to express the power spectrum in dimensionless form, as the variance per logarithmic interval in k;

${△}^2(k)=\frac{d\langle {\delta }^2\rangle }{dlnk}\infty k^{3}P(k)$ (23)

${△}^2(k)=\frac{2}{\pi }{k}^3{\displaystyle \int \xi (r)\frac{\sin kr}{kr}{r}^{2}dr}$ (24)

This formulation gives more intuitive meaning to the power spectrum than just P(k), which is the functional representation of power per unit volume in kspace. For example ∆²(k) = 1 means there are order unity density fluctuations from modes in the logarithmic bin around wavenumber [20] k.

In ΛCDM (Lambda Cold Dark Matter model) the initial power spectrum of density fluctuations is nearly scale-invariant, which means that fluctuations were almost equally strong at all spatial scales. The power spectrum is often represented as:

P(k) ∝ k^ns (25)

Where k is the wavenumber of fluctuations.

n_s is the spectral index.

The primordial spectrum, especially from inflationary models, predicts that the fluctuations are nearly scale-invariant, with a spectral index n_s ≈ 1(HarrisonZeldovich spectrum). This scale-invariant spectrum is modified over time by the expansion of the Universe, gravitational collapse, and dark energy. The transfer function is used to modify the primordial power spectrum to account for these effects, yielding the matter power spectrum observed today. As the Universe expands, different cosmological epochs (radiation-dominated, matter-dominated, dark energy-dominated) influence the growth of fluctuations. In the radiation-dominated era, sound waves in the photon-baryon fluid set the scale for fluctuations and suppress the growth of structure on small scales, leading to a suppressing effect at high k. During the matter-dominated era, gravitational collapse becomes more efficient, and density fluctuations grow, amplifying the initial power spectrum at large scales. In the dark energy-dominated era, the expansion of the Universe accelerates, slowing the growth of structures at large scales, and leading to a flattening of the power spectrum at very low [17] k. The matter power spectrum at z = 0 (today) is often derived from the primordial power spectrum by applying a transfer function T(k);

P(k,T) = P(k)T(k,z)² (26)

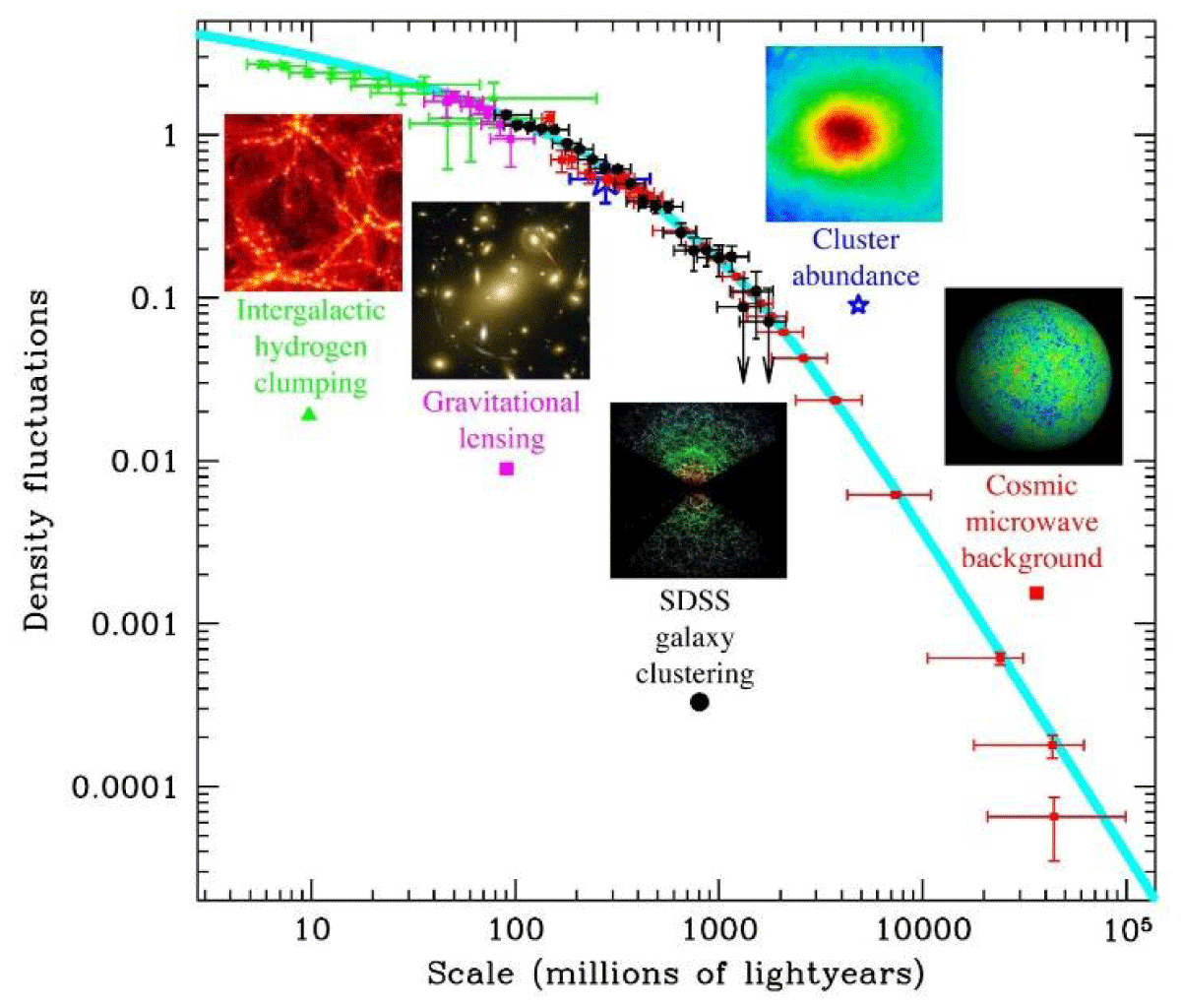
Where, T(k,z) is the transfer function, which modifies the primordial power spectrum by accounting for the effects of cosmic expansion, baryon-photon drag, and gravitational collapse Figure 2.

Using the dimensionless form of the power spectrum with the suitable cosmological parameters of the ΛCDM model the power spectrum of density fluctuations, the distribution of galaxies, and the evolution of cosmic structures can be traced over four orders of magnitude, from the scales of a few M_pc via intergalactic Lyman alpha clouds, weak gravitational lensing and CMB fluctuations [21] as in 2:

In the early Universe, density fluctuations (encoded in the initial power spectrum) were small. These fluctuations were seeded by quantum processes during inflation, with different scales of fluctuation having different amplitudes and shapes. These initial fluctuations were imprinted on the Cosmic Microwave Background (CMB), which provides a snapshot of the early Universe’s power spectrum. The evolution of these initial fluctuations, influenced by the expansion of the Universe and the transition from radiation-dominated to matter-dominated and dark energy-dominated eras, ultimately led to the growth of structures. As the fluctuations grow, they evolve into different types of Chaos in the Cosmos: Quantum Whispers and The Cosmic Genesis of Structures. The power spectrum quantifies how much variance exists in fluctuations across different scales, and it plays a key role in determining what kinds of structures emerge. The two-point correlation function ξ(r) provides a direct description of the clustering of galaxies and other objects in real space. It reveals the spatial distribution of matter. These two statistical measures along with the influence of cosmological parameters like matter density (Ωm), Dark energy density (ΩΛ), and Hubble constant (H₀) tell us how the growth of density fluctuations leads to structure formation.

4.1 On large scales

On large scales (Small k), the fluctuations in the density field are initially small and linear, thereby corresponding to the linear regime in the evolution of the cosmos. These perturbations are nearly scale-invariant, meaning they are roughly the same across all spatial scales. This linear growth means that the density field responds in proportion to the initial perturbations. Gravity is not strong enough on large scales to cause rapid collapse of structures due to Hubble flow. The power spectrum on large scales is dominated by the contribution of dark matter and baryons, but the gravitational effects on these scales are relatively weak. The fluctuations here do not lead to fast gravitational collapse but rather to the slow formation of large structures (like superclusters and voids) as the Universe evolves. On large scales (small k long wavelengths), the fluctuations are mostly of small amplitude, and the power spectrum P(k) is relatively flat or follows a gentle slope. These scales correspond to large regions of the Universe, where the density perturbations are weak. The long-wavelength modes (larger and small k) are responsible for the global distribution of matter. For instance, the largest structures in the Universe, such as filaments and voids, are shaped by these long-wavelength perturbations. The density fluctuations on these scales correspond to the cosmic web structures shaped purely by the constituents of dark matter that emerge later and hence form the backbone of the cosmic web. On the same scales, the two-point correlation function ξ(r) becomes flattened or approaches zero. This means that the density fluctuations on these scales are weak, and there is little clustering of galaxies on the largest scales. Instead, the matter is more uniformly distributed, leading to a more homogenous appearance when viewed at very large distances [11,22].

4.2 On small scales

As structure formation progresses, the fluctuations on smaller scales (larger k) grow faster, eventually entering a non-linear regime. The power spectrum shows a turnover at a particular wavenumber, corresponding to the non-linear scale. This is the point where the fluctuations no longer grow linearly but instead undergo non-linear collapse, forming compact structures. As the fluctuations increase in amplitude and regions of higher density become gravitationally bound, the growth rate of the density contrast (δ) becomes faster and more complex. These regions of over-density eventually form compact structures, such as galaxies, galaxy clusters, and dark matter halos. Non-linear growth results in the formation of overdense regions that collapse and become dark matter halos. These halos are the gravitational wells in which galaxies are formed. At smaller scales (large k), the power spectrum P(k) steepens because gravitational collapse leads to rapid amplification of fluctuations. Small-scale fluctuations grow faster due to the efficient clustering of dark matter. The dark matter halos and galaxies that form from these fluctuations correspond to the smaller scales in the power spectrum. While as, on small scales, the two-point correlation function ξ(r) increases significantly because galaxies and dark matter halos are much more likely to be found close to each other. This reflects the fact that gravitational collapse causes objects to form dense clumps [23]. As a result, the correlation function shows a sharp increase at small separations, indicating high clustering. As we go to smaller separations, ξ tends to saturate or flatten, because objects (such as galaxies or dark matter halos) cannot get infinitely close to each other due to the finite size of galaxies and the core of dark matter halos (saturation r ~ 1 − 2M_pc. This behavior is important for understanding the dynamic interactions between structures at very small scales. The two-point correlation function also reveals characteristic length scales as;

r ~ 1 − 2M_pc (27)

This corresponds to the size of typical galaxy groups or small clusters, hence ξ shows a peak, indicating that galaxies tend to cluster readily at these scales. These scales provide insight into the hierarchical nature of structure formation, where galaxies and dark matter halos form first, and then larger structures, such as groups, clusters, and the cosmic web, emerge through gravitational interactions [13].

In summary, the process of structure formation in the universe is driven by the gravitational collapse of initial density fluctuations, as evidenced by the power spectrum P(k) and two-point correlation function ξ(r). On large scales, the universe exhibits a cosmic web structure, where galaxies and clusters form along filaments, with vast voids in between. On smaller scales, structure formation is characterized by the collapse of dark matter halos, leading to the formation of galaxies and their subsequent clustering into galaxy groups and clusters. The power spectrum P(k) provides a quantitative description of these fluctuations across different scales, while the correlation function ξ(r) captures the clustering properties of matter. Observational data, such as the CMB, galaxy surveys, and numerical simulations, confirm the hierarchical nature of structure formation and the evolution of large-scale structures, influenced by the interplay of dark matter, dark energy, and gravitational dynamics.

1. Martinez E, Hidalgo CA. Primordial structures and their quantum origins. J Mod Phys. 2022. Available from: https://www.scirp.org/journal/paperinformation?paperid=46224
2. Kumar KS, Marto J. A robust explanation of CMB anomalies with a new formulation of inflationary quantum fluctuations. arXiv. 2023. Available from: https://arxiv.org/abs/2305.06057
3. Mukhanov VF, Feldman HA, Brandenberger RH. Theory of cosmological perturbations. Phys Rep. 1992;215(5-6):203-333. Available from: https://www.sciencedirect.com/science/article/pii/037015739290044Z
4. Porcelli F, Scibona G. Large-scale structure formation via quantum fluctuations and gravitational instability. Int J Geosci. 2014;5. Available from: https://www.scirp.org/journal/paperinformation?paperid=46224
5. Baumann D, Peiris HV. Cosmological inflation: Theory and observations. arXiv. 2008. Available from: https://arxiv.org/abs/0810.3022
6. Lyth D H, Liddle AR. The primordial density perturbation: Cosmology, inflation and the origin of structure. Cambridge: Cambridge University Press; 2009. Available from: https://www.cambridge.org/core/books/primordial-density-perturbation/F31CB0303093E5871D3DB103E9714E5C
7. Sasaki M. Large-scale quantum fluctuations in the inflationary universe. Prog Theor Phys. 1986;76(5):1036-1046. Available from: https://doi.org/10.1143/PTP.76.1036
8. Guth AH, Kaiser DI. Inflationary cosmology: Exploring the universe from the smallest to the largest scales. Science. 2005;307(5711):884-890. Available from: https://www.science.org/doi/abs/10.1126/science.1107483
9. Pen UL, Seljak U, Turok N. Power spectra in global defect theories of cosmic structure formation. Phys Rev Lett. 1997;79:1611. Available from: https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.79.1611
10. Landau S, León G, Sudarsky D. Quantum origin of the primordial fluctuation spectrum and its statistics. Phys Rev D. 2013;88(2):023526. Available from: https://journals.aps.org/prd/abstract/10.1103/PhysRevD.88.023526
11. Labini FS. Gravitational clustering: an overview. In: AIP Conference Proceedings. American Institute of Physics. 2008:970;205-221. Available from: https://arxiv.org/abs/0806.2560
12. Guth AH, Pi SY. Fluctuations in the new inflationary universe. Phys Rev Lett. 1982;49:1110-1113. Available from: https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.49.1110
13. Davis R, Zhou K. A new paradigm in density perturbations during inflationary phases. Universe Res J. 2023.
14. Maldacena J. Non-gaussian features of primordial fluctuations in single field inflationary models. JHEP. 2003;2003(05):013. Available from: https://doi.org/10.1088/1126-6708/2003/05/013
15. Morikawa M. Quantum fluctuations in vacuum energy: Cosmic inflation as a dynamical phase transition. Universe. 2022;8(6):295. Available from: https://doi.org/10.3390/universe8060295
16. Steinhardt PJ. Natural inflation. In: Gibbons GW, Hawking SW, Siklos STC, editors. The Very Early Universe. Cambridge: Cambridge University Press; 1983;251.
17. Scoccimarro R, Zaldarriaga M, Hui L. Power spectrum correlations induced by nonlinear clustering. Astrophys J. 1999;527(1):1. Available from: https://arxiv.org/abs/astro-ph/9901099
18. Bharadwaj S. Perturbative growth of cosmological clustering II: The two-point correlation.
19. Zhang Y. A coarse-grained field theory for density fluctuations and correlation functions of galaxies and clusters. Astron Astrophys. 2007;464(3):811-814. Available from: https://arxiv.org/abs/astro-ph/0611712
20. Zhang Y, Chen Q, Wu SG. Field theory of the correlation function of mass density fluctuations for self-gravitating systems. Res Astron Astrophys. 2019;19(4):053. Available from: https://arxiv.org/abs/2107.09425
21. Kitaura FS. Non-gaussian gravitational clustering field statistics. Mon Not R Astron Soc. 2012;420(4):2737-2755. Available from: https://doi.org/10.1111/j.1365-2966.2011.19680.x
22. Achúcarro A, Gong JO, Palma GA. Non-gaussianity in the era of precision cosmology. Prog Theor Phys. 2023.
23. Parker LE, Fulling SA. Exploring high-energy density fluctuations in cosmology. J Astrophys. 2021.