More Information
Submitted: July 05, 2024 | Approved: July 15, 2024 | Published: July 16, 2024
How to cite this article: Petersen-Sonn EA, Jespersen MF, Johnson MS, Mikkelsen KV. Mechanistic Insights into UV Spectral Changes of Pyruvic Acid and Pyruvate Part 1: Interaction with Water Molecules. Int J Phys Res Appl. 2024; 7(2): 100-107. https://dx.doi.org/10.29328/journal.ijpra.1001092
DOI: 10.29328/journal.ijpra.1001092
Copyright License: © 2024 Petersen-Sonn EA, et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Keywords: Pyruvic acid; Water cluster; UV-VIS; TD-SCF
Mechanistic Insights into UV Spectral Changes of Pyruvic Acid and Pyruvate Part 1: Interaction with Water Molecules
Emma A Petersen-Sonn, Malte F Jespersen, Matthew S Johnson, and Kurt V Mikkelsen*
Department of Chemistry, University of Copenhagen, Universitetsparken 5, DK-2100 Copenhagen Ø, Denmark
*Address for Correspondence: Kurt V Mikkelsena, Department of Chemistry, University of Copenhagen, Universitetsparken 5, DK-2100 Copenhagen Ø, Denmark, Email: [email protected]
We investigate how the UV spectra of pyruvic acid (PA) and pyruvate are impacted by interactions with water molecules. In particular, we would like to understand the mechanistic origin of the blue shift in the n →− π* transition. Pyruvic acid is the simplest α-keto organic acid and is common in the environment. We use density functional theory to optimize geometries to determine excitation energies and find that the excitation energies of the two main pyruvic acid conformers and pyruvate blue shift when interacting with 1 to 4 water molecules, both in vacuo and in a solvent. The excitation wavelength is blue-shifted by 0.9-9.2 nm when adding water molecules to the lowest energy conformer of PA. Calculations of the UV spectra of pyruvic acid (PA) and pyruvate are crucial for understanding the impact of the interactions with water molecules.
The powerful influence of interfaces on molecular properties has driven research on the unique photochemistry occurring on water surfaces like the ocean and aerosol particles [1-4]. Pyruvic Acid (PA) is a compelling test system. It is commonly found in the environment and biological systems.
In the atmosphere, it occurs in the gas phase and aerosols and droplets produced e.g. in the oxidation of isoprene. In addition to being important in its own right, as the simplest α-keto organic acid it is a good representative of this class of compounds. We perform investigations of the UV spectra of Pyruvic Acid (PA) and pyruvate to understand how the spectra are influenced by the interactions with water molecules. This is crucial for understanding how the molecular compounds can include water molecules in their structures and form the starting structures of clusters forming aerosol particles at a later stage.
The presence of a keto-group in the α position to an organic acid gives rise to an electronic transition accessed by UV sunlight; organic acids are otherwise not generally photoactive. PA has a continuous absorption band with a significant diffuse vibrational structure that extends from 275 to 400 nm, peaking near 350 nm [5-8]. There are four exit channels for gas phase photolysis:
CH3COCOOH + hν −→ CH3CHO + CO2 ϕ1 = 48 ± 1 %
CH3CO + COOH ϕ2 = 39 ± 10 %
CH3COOH + CO ϕ3 = 8 ± 13 %
CH3CO + CO + OH ϕ4 = 5 ± 3 %
Photolysis is the major loss process for PA in the atmosphere. Mellouki and Mu estimate the chemical lifetime concerning the gas-phase OH reaction is more than 3 months, and a few hours for photolysis (gas-phase) [6].
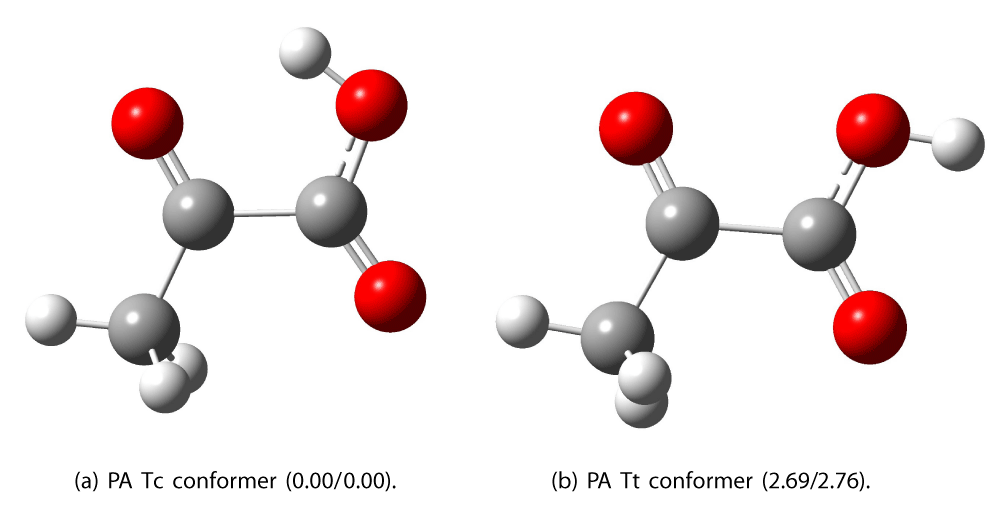
Blair, et al. identified four stable conformers of pyruvic acid, Tc, Tt, Ct, and Cc with energies of 0.0, 2.68, 4.36, and 10.31 kcal/mol respectively [9].
The first letter of the label refers to the cis or trans relative orientation of the carbonyl groups and the second, the cis or trans orientation of the acidic hydroxyl relative to the ketonic carbonyl. Here we consider the two lowest energy forms, Tc and Tt. These two conformers differ in that the orientation of the hydroxyl group is either cis or trans to the ketonic oxygen. When investigating pyruvate, these conformers cease to exist because the negative charge is fully delocalized between the two oxygen atoms in the acid group.
Hence, only one conformer of pyruvate is investigated in this study.
Calculations
We investigate the excitation energies and UV-VIS spectra of PA and pyruvate from the gas phase to bulk via molecular clusters with discrete water molecules and interactions with a water cluster surface. Geometries were optimized using the ωB97X-D [10] and CAM-B3LYP [11] functionals, using the aug-cc-pVTZ (AVTZ) basis set [12]. Calculations were performed using Gaussian16 [13]. Water molecules were added sequentially optimizing the structures with each step. Several possibilities for the positions of the water molecules were explored, and the geometry with the lowest ground state energy was chosen for further work. Four water molecules were added in total.
We note that the cluster formations depend on the different conformations which is similar to previous investigations [14-16]. Furthermore, the calculated UV-Vis spectra exhibit a clear trend concerning the inclusion of water molecules in the molecular clusters. The electronic transitions get more blueshifted with an increasing number of water molecules. This observetion can be utilized when undertaking experimental investigations of clusters containing organic acids and water molecules. Investigations, such as the ones presented here, are of importance for understanding the formation of molecular clusters and previous investigations have clearly shown this [14-16].
The level of theory utilized in this article has previously been shown to be sufficient accuracy when compared to experimental data and more accurate theoretical models [14-16]. Pyruvic Acid (PA) has several conformers; the Tc and the Tt conformers are dominant [17,18]. These two lowest-energy conformers are shown in Figure 1. The labels Tc and Tt follow the nomenclature used in previous studies [9,17]. The relative energies of the conformers are also shown in the Figure. We find the energy of the Tt conformer is 2.69 kcal/mol above the Tc conformer calculated with CAM-B3LYP/AVTZ. A determination by Blair, et al. found Tt to be 1.96 kcal/mol [9] above the Tc conformer. We believe the difference is largely due to the difference in the method. We report a value calculated using DFT whereas Blair, et al. calculated the energy based on CCSD(T)/ωB97X-D/AVTZ. The CCSD(T) method is known to give highly accurate single-point energies [19].
Figure 1: Optimized structures (at the CAM-B3LYP/AVTZ level of theory) of the two lowest energy conformers of pyruvic acid. The relative energies in kcal/mol, calculated with CAM-B3LYP/AVTZ (normal font), and ωB97X-D/AVTZ (italic font), are shown in parentheses.
Work by Shemesh, et al. [17] has shown that pyruvate is the most dominant structure in solution at pH values ranging from 2.9 to 7.9. For this reason, pyruvate is included in this study, along with PA in its Tc and Tt conformers.
We investigate the association of water molecules with these three species.
Water molecules are added sequentially to the given conformer of PA or pyruvate, and the structure of each cluster is optimized. Another water molecule is added after the lowest ground state energy has been located. Up to four water molecules were added to the PA conformers. The water molecules migrate to the oxygen atoms as these are the most polar areas and the water molecules can form hydrogen bonds. Because of these effects, the search for the lowest ground state energy of the complexes is initiated by placing water molecules near the different oxygen atoms.
The optimized structures of the PA conformers interacting with 1 to 4 water molecules were used in TD-SCF calculations to obtain excitation energies. In this study, we investigate the excitation energies of the PA, Tc and Tt conformers and pyruvate. First, we present each of the three species and then a summary and discussion.
Pyruvic acid Tc ketone
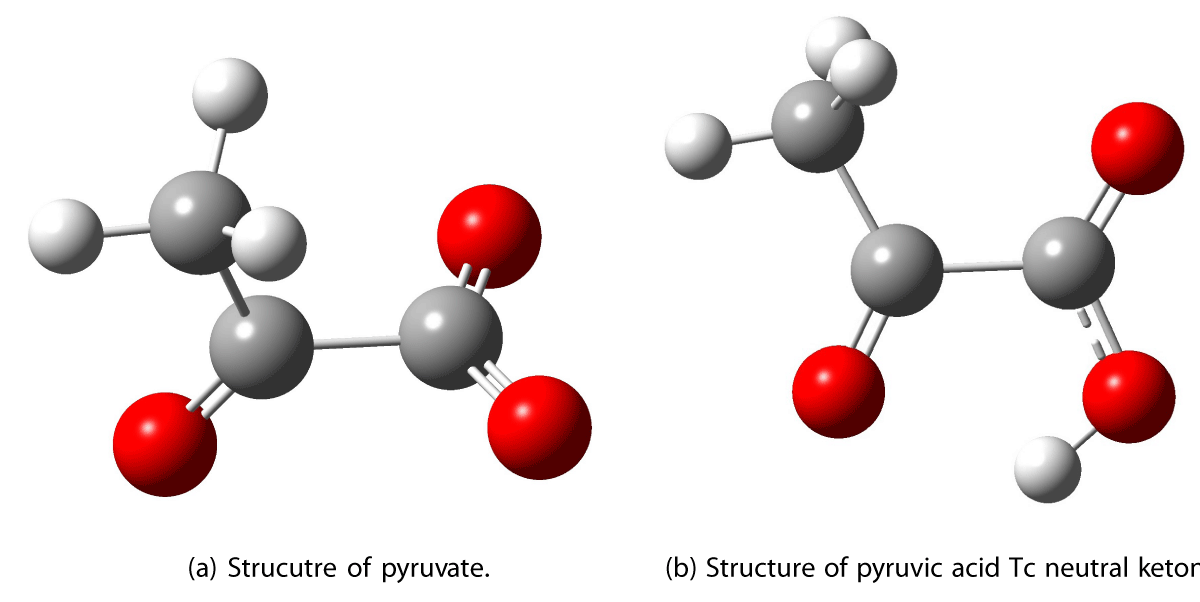
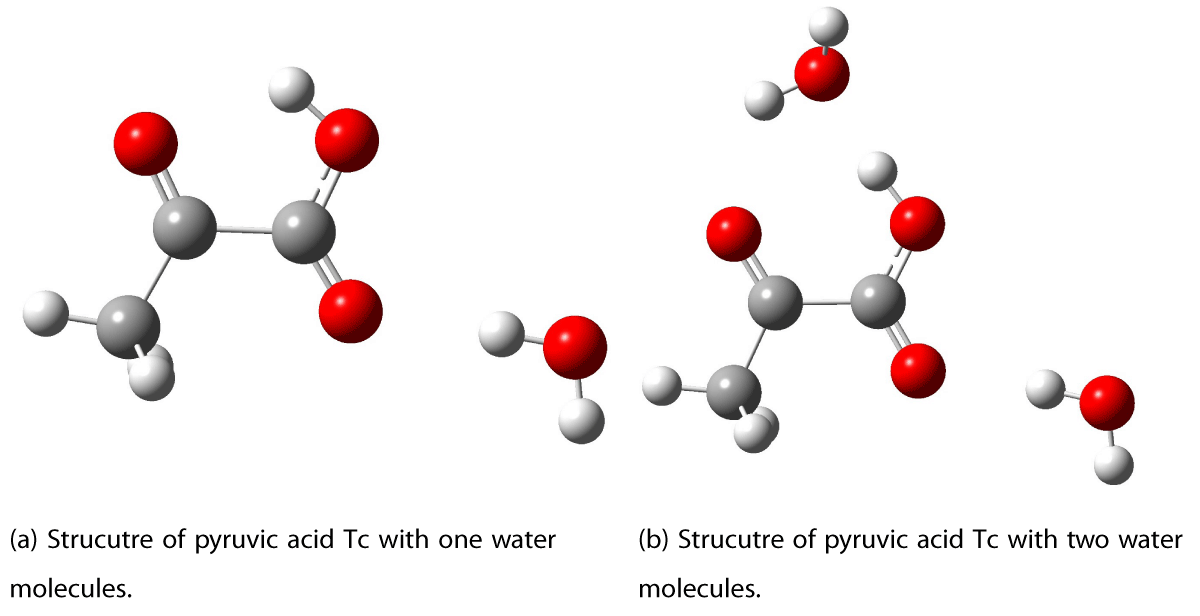
The optimized geometry of the pyruvic acid Tc conformer in vacuum is shown in Figure 2. Different possible structures for the addition of a water molecule were investigated and the resulting lowest energy structure is shown in Figure 3a. In previous research, a different structure for the addition of the first water molecule was suggested in which the water molecule is hydrogen bonded to the hydroxyl group and the ketonic oxygen [9,17]. This position for the first water molecule was investigated in this study and was not found to have the lowest ground-state energy. The position for the first water molecule suggested in previous literature was found to be 3.38 kcal/mol higher in energy than the geometry presented in Figure 3a,b. The second water molecule is added at a position where a hydrogen bond is formed from the hydroxy group in pyruvic acid to the oxygen lone pair in water. An additional hydrogen bond is formed from the hydroxy group of water to the ketonic oxygen of PA.
Figure 2: Optimized structures of pyruvate and PA Tc neutral ketone. Calculated with CAM-B3LYP/AVTZ.
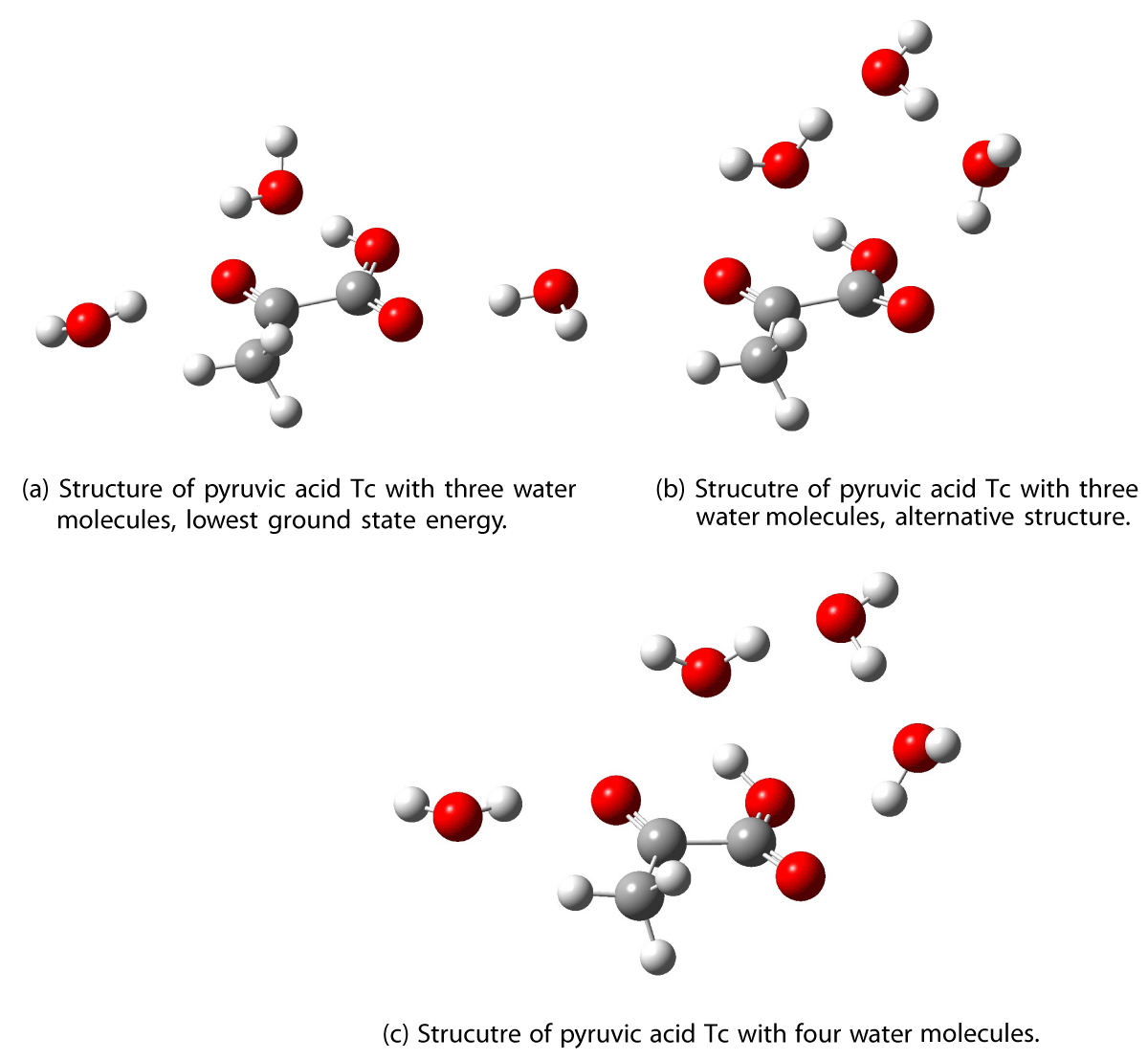
Optimizations with up to four water molecules around the pyruvic acid Tc conformer was performed, the resulting structures are shown in Figure 3 and 4.
Figure 3: Optimized structures of PA Tc ketone with 1 and 2 water molecules. Calculated with CAM-B3LYP/AVTZ.
Figure 4: Optimized structures of PA Tc neutral ketone with three and four water.
The third water molecule can be positioned either hydrogen bonded to the ketonic oxygen in PA or the first and second water molecules. The former structure (Figure 4a) is found to have the lowest energy in the ground state with an energy difference of 7.91 kcal/mol relative to the latter structure (Figure 4b). The excitation wavelengths for the structure shown in Figure 4b are included in Table 1 to compare the two different structures with three water molecules.
| Table 1: Summary of excitation wavelengths for the pyruvic acid Tc conformer with 1, 2, 3, and 4 water molecules, in vacuo and solvent (water). The energies were calculated with the functionals CAM-B3LYP and ωB97X-D and the AVTZ basis set. aStructure with the lowest energy. bAlternative structure with water molecules primarily hydrogen bonded to each other. |
|||||
| Medium | # of H2O | CAM-B3LYP | ωB97X-D | ||
| λ / nm | Osc. | str. λ / nm | Osc. str. | ||
| vacuum | 0 | 345.9 | 0.0000 | 348.8 | 0.0000 |
| 1 | 340.6 | 0.0000 | 343.1 | 0.0000 | |
| 2 | 336.7 | 0.0001 | 345.5 | 0.0001 | |
| 3a | 338.1 | 0.0000 | 341.0 | 0.0000 | |
| 3b | 345.0 | 0.0001 | 347.7 | 0.0001 | |
| 4 | 338.2 | 0.0001 | 342.4 | 0.0001 | |
| water | 0 | 337.1 | 0.0001 | 340.0 | 0.0001 |
| 1 | 332.9 | 0.0000 | 335.4 | 0.0000 | |
| 2 | 336.8 | 0.0001 | 339.4 | 0.0001 | |
| 3a | 330.7 | 0.0000 | 332.8 | 0.0000 | |
| 3b | 341.3 | 0.0001 | 344.2 | 0.0001 | |
| 4 | 334.1 | 0.0001 | 337.2 | 0.0001 | |
Table 2 shows an experimental value, several theoretical literature values, and values from this study, for the excitation wavelengths of the PA Tc conformer. Shemesh et al. report wavelengths of 358 and 351 nm based on calculations using the cc-pVDZ and def-SV(P) basis sets respectively, along with the ADC(2) method. The difference in excitation energy is likely due to the choice of method. Shemesh, et al. used the ADC(2) method with a 124 cc-pVDZ basis set, whereas this study used the TD-SCF method with the aug-cc-pVDZ basis set (and two different functionals). It was earlier demonstarted [20] that the TD-SCF method tends to underestimate the excitation energies, for example, ωB97X-D shows a Mean Signed Error (MSE) of -0.213 eV and CAM-B3LYP show an MSE of -0.238 eV concerning CC3. The article also provides errors for TD-SCF methods compared to ADC(2), and here they show MSEs of -0.242 eV and -0.267 eV for ωB97X-D and CAM-B3LYP, respectively [20].
| Table 2: Comparison of PA Tc excitation wavelengths with literature. Calculations performed in a vacuum. | |||
| λ / nm | Osc. strength | Method | Ref. |
| 350 | - | exp./gas phase | [22] |
| 358 | 0.00000035 | ADC(2)/cc-pVDZ | [17] |
| 351 | 0.00000355 | ADC(2)/def-SV(P) | [17]∗ |
| 351 | - | TD-SCF/CAM-B3LYP/6-31G* | [21] |
| 354 | - | TD-SCF/ωB97X-D/6-31G* | [21] |
| 345.9 | 0.0000 | TD-SCF/CAM-B3LYP/AVTZ | this work |
| 348.8 | 0.0000 | TD-SCF/ωB97X-D/AVTZ | this work |
| ∗ In the supporting information of the article. | |||
Chang, et al. [21] report several excitation energies calculated with the TDSCF method and the 6-31G* basis set, with values of 351 and 354 nm for 134 the CAM-B3LYP and ωB97X-D functionals, respectively.
Both wavelengths calculated in this study are longer than the previous literasure values. The result from the ωB97X-D/AVTZ method is only 1.2 nm from the experimental value, while the CAM-B3LYP/AVTZ result is 4.1 nm from the experimental value. Hence for the PA Tc conformer in a vacuum with no water, the ωB97X-D/AVTZ method provides the more precise result of the two methods applied in this study.
In Table 3, results for zero to four water molecules in vacuo are compared with the results of Shemesh, et al. [17]. For the addition of more water molecules, the ωB97X-D functional yields values closest to those of Shemesh, et al. The differences in energy between the values reported by Shemesh, et al. and this study are significantly larger for the structure with one water molecule than for no water molecules. As mentioned this study and Shemesh, et al. disagree on the position of the first water molecule. It is expected that these two different positions would cause different excitation energies.
| Table 3: Comparison of the effect of the addition of zero to four water molecules to the pyruvic acid Tc conformer on transition wavelength, in vacuo. The values from this study were calculated using the TD-SCF method, with the given functional and the AVTZ basis set. | ||||
| # H2O | λ / nm | Osc. strength | Method | Ref. |
| 0 | 350 | 4E-07 | ADC(2)/cc-pVDZ | [17] |
| 346 | 0 | CAM-B3LYP | this work | |
| 349 | 0 | ωB97X-D | this work | |
| 1 | 364 | 4E-06 | ADC(2)/cc-pVDZ | [17] |
| 341 | 0 | CAM-B3LYP | this work | |
| 352 | 0 | ωB97X-D | this work | |
| 2 | 359 | 4E-06 | ADC(2)/cc-pVDZ | [17] |
| 337 | 0.0001 | CAM-B3LYP | this work | |
| 346 | 0.0001 | ωB97X-D | this work | |
| 3 | 359 | 6E-05 | ADC(2)/cc-pVDZ | [17] |
| 338 | 0 | CAM-B3LYP | this work | |
| 341 | 0 | ωB97X-D | this work | |
| 4 | 347 | 0.0002 | ADC(2)/cc-pVDZ | [17] |
| 338 | 0.0001 | CAM-B3LYP | this work | |
| 342 | 0.0001 | ωB97X-D | this work | |
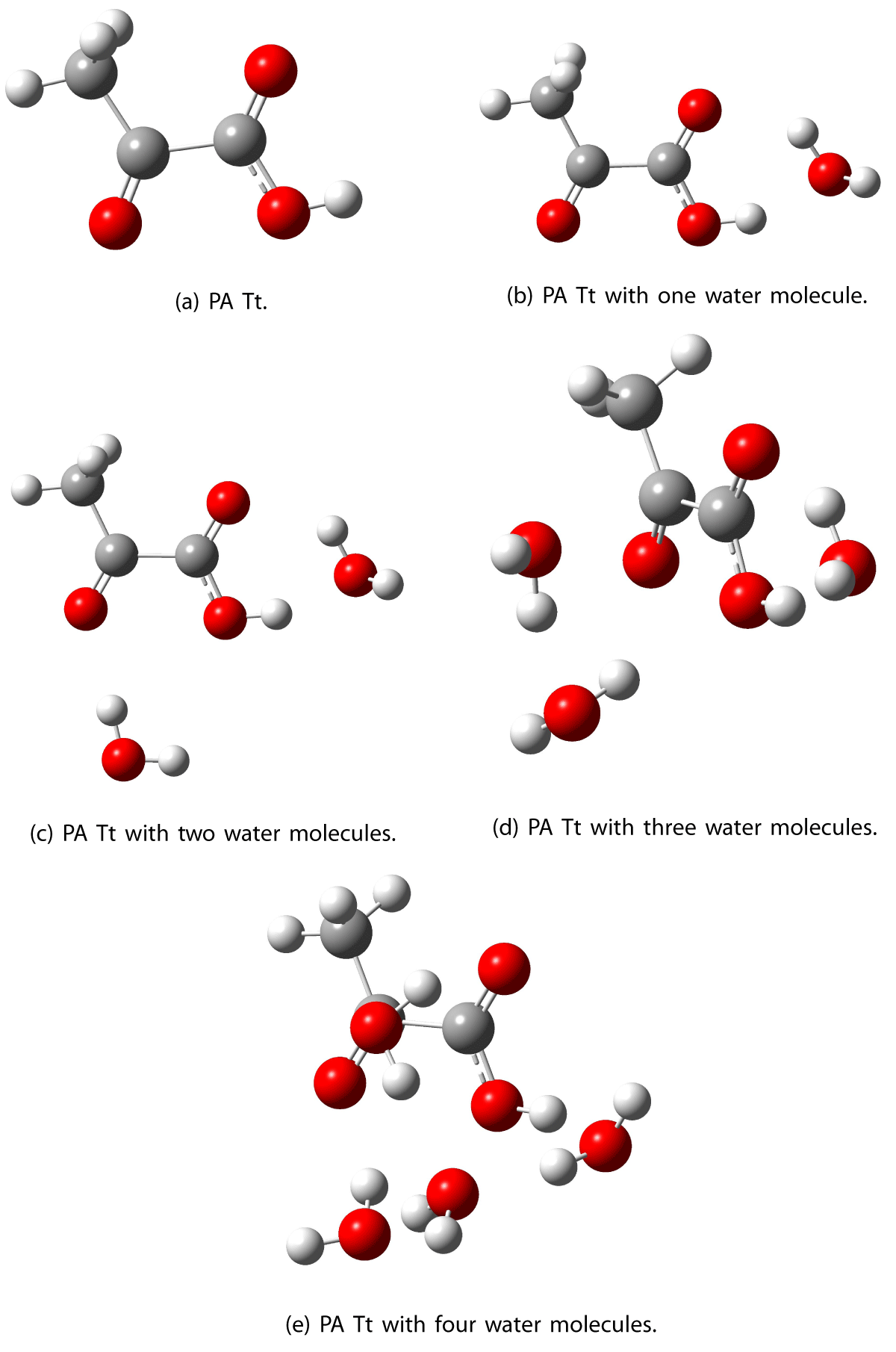
Pyruvic acid Tt conformer
The geometries for pyruvic acid Tt conformer and up to four water molecules were optimized in vacuo and water, see Figure 5. As shown in Table 4, when individual water molecules are added to the Tt conformer of pyruvic acid, the excitations shift to shorter wavelengths, i.e. 155 higher energy. This is an effect that is observed in a vacuum and a dielectric medium (water). The trend is especially evident in a vacuum, where a blue shift of 2.4, 9.5, 19.7, and 21.8 nm for 1 to 4 water molecules respectively is 158 observed.
Figure 5: Optimized structures of the lowest energy structure of PA Tt with up to four water molecules.
| Table 4: Summary of excitation wavelengths and oscillator strengths for the lowest energy conformer of pyruvic acid Tt with 1, 2, 3, and 4 water molecules, in vacuo and water solvent, calculated with CAM-B3LYP/AVTZ and ωB97X-D/AVTZ. | |||||
| Medium | # of H2O | CAM-B3LYP | ωB97X-D | ||
| λ / nm | Osc. str. | λ / nm | Osc. str. | ||
| vacuum | 0 | 354.8 | 0.0001 | 357 | 0.0000 |
| 1 | 352.4 | 0.0000 | 354.7 | 0.0000 | |
| 2 | 345.3 | 0.0001 | 346.8 | 0.0001 | |
| 3 | 335.1 | 0.0000 | 333.1 | 0.0001 | |
| 4 | 333.0 | 0.0001 | 329.6 | 0.0001 | |
| water | 0 | 346.6 | 0.0001 | 348.9 | 0.0001 |
| 1 | 346.8 | 0.0001 | 349.2 | 0.0001 | |
| 2 | 339.7 | 0.0001 | 342.3 | 0.0001 | |
| 3 | 336.6 | 0.0000 | 339.4 | 0.0001 | |
| 4 | 333.7 | 0.0000 | 336.1 | 0.0001 | |
Shemesh, et al. report excitation values for the PA Tt conformer with no water molecules in vacuo [17]. These are compared to the results from our study in Table 5. We find excitation wavelengths that are 6 to 8.2 nm longer (lower energy) than those reported by Shemesh, et al. As mentioned previously, the TD-SCF methods generally underestimate excitation energies 164 and we take them as a lower limit on the true excitation energy. We also note that the ADC(2)/cc-pVDZ method uses a basis set with no diffuse functions whereas the aug-cc-pVTZ basis set used in this study does contain diffuse functions [12]; the functionals ωB97X-D and CAM-B3LYP will be better able to describe long-range interactions [10,11], useful for example in describing how the dipole moment changes when adding water molecules or a solvent 170 model.
| Table 5: Comparison of pyruvic acid Tt conformer excitation wavelengths and oscillator strengths found in this work and the literature. | |||
| λ / nm | Osc. strength | Method | Ref. |
| 363 | 0.00000077 | ADC(2)/cc-pVDZ | [17] |
| 354.8 | 0.0001 | TD-SCF/CAM-B3LYP/AVTZ | this work |
| 357.0 | 0.0000 | TD-SCF/ωB97X-D/AVTZ | this work |
Pyruvate
The geometries for pyruvate alone and with individual water molecules are shown in Figures 6 and 7. The dihedral angle between the ketonic oxygen and acid carbonyl groups in pyruvate is twisted by about 900 compared to PA. Shemesh, et al. [17] previously investigated pyruvate in solution, although geometries from their calculations did not show the same ”twist” until adding the third water molecule. This difference could be due to the electronic structure method chosen for the calculations. The geometries in Figure 6 is calculated with a DFT method (CAM-B3LYP/AVTZ), whereas the results from Shemesh, et al. were calculated with MP2/cc-pVDZ. The cc-pVDZ basis set does not include diffuse functions, which are included in the calculations in this study when using the aug-cc-pVTZ basis set. The method applied by Shemesh, et al. furthermore contains a basis set with a double zeta valence. Compared to the triple zeta valence in the basis set used in this study, it is expected to provide a lower percentage of the total valence correlation energy. According to Ref. [23], the cc-pVDZ basis set can provide approximately 65% of the total correlation energy, while the cc-pVTZ basis set can provide 85%. Therefore, it is possible that the method used by Shemesh, et al. without the diffuse functions, did not capture the interactions involving the ”twisted” pyruvate with zero to two water molecules.
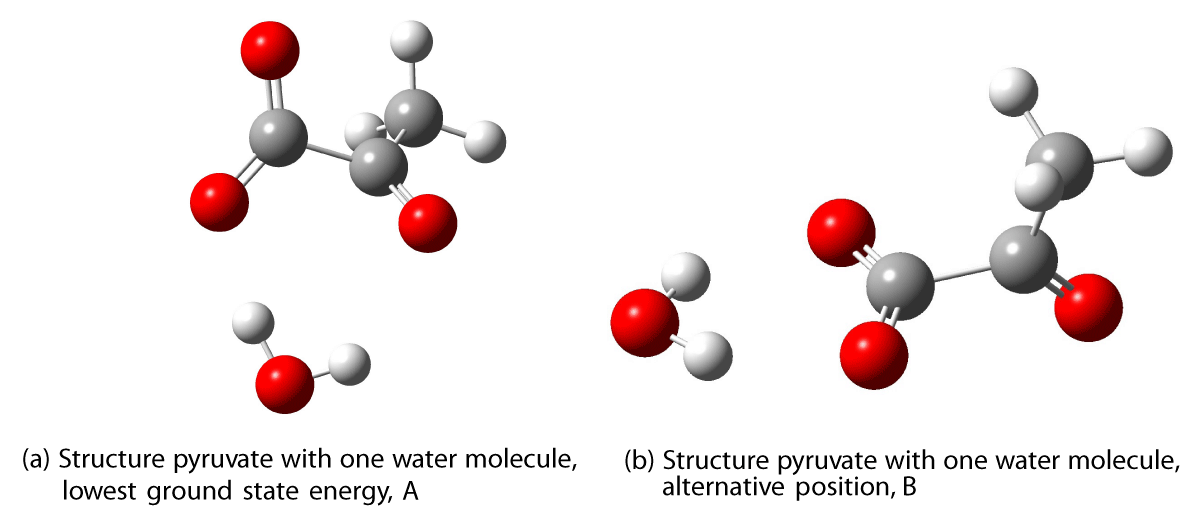
Figure 6: Optimized structures of pyruvate with one water molecule. Calculated with CAM-B3LYP/AVTZ.
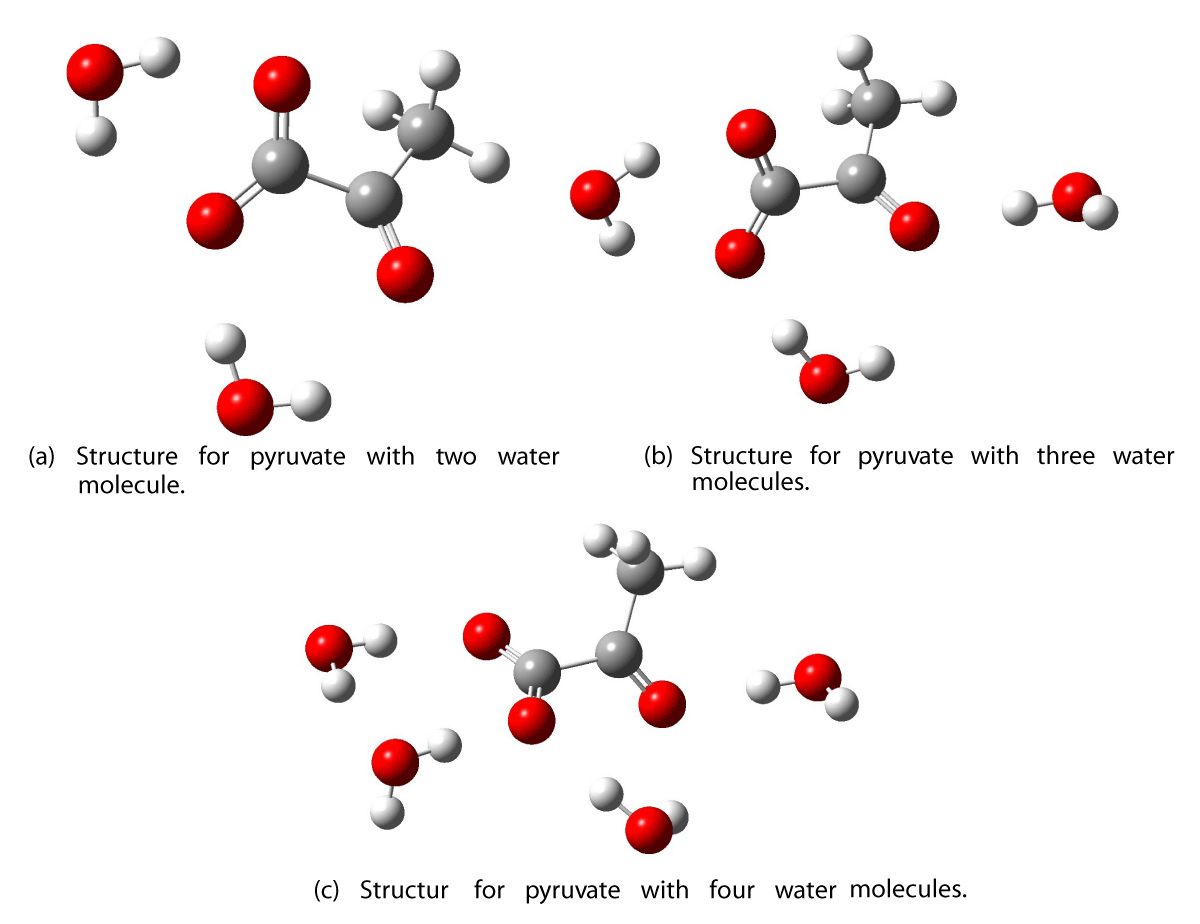
Figure 7: Optimized structures of pyruvate with two, three, and four water molecules.
We investigated two positions for the first water molecules. Both have the water molecule bonded to two oxygen atoms in pyruvate. The position for the water molecule with the lowest total energy of the ground state, labeled A, has the water molecule interacting with both the ketonic and one of the oxygen atoms in the carboxylate group simultaneously, as shown in Figure 6a. The other position, labeled B, is approximately 1 kcal/mol higher in energy and has two hydrogen bonds from the water to the two carboxylate oxygen atoms in pyruvate, as seen in Figure 6b.
A large difference in the excitation energies is seen for these two geometries including the first water molecule. The structure with the lowest ground state energy calculated with CAM-B3LYP/AVTZ in vacuum (6a) has an excitation wavelength of 328.2 nm, while the other (6b) has an excitation energy of 304.1 nm in a vacuum. The experimental value for the excitation energy in water is 320 nm, cf. Table 6 [17]. The excitation energies calculated in water are blueshifted 21 to 24 nm relative to the experimental value.
| Table 6: Comparison of pyruvate excitation values with literature. The values from this study were calculated using the TD-SCF method, with the given functional and the aug-cc-pVTZ basis set. | ||||
| λ / nm | Osc. strength | Method | Medium | Ref. |
| 390 | 0.00000638 | ADC(2)/cc-pVDZ | vacuum | [17] |
| 382 | 0.00004174 | ADC(2)/def-SV(P) | vacuum | [17] ( SI ) |
| 312 | 0.0004 | CAM-B3LYP | vacuum | this work |
| 315 | 0.0005 | ωB97XD | vacuum | this work |
| 296 | 0.0005 | CAM-B3LYP | water | this work |
| 299 | 0.0006 | ωB97XD | water | this work |
| 320 | – | experimental | water | [17] |
Dramatically, structure A has an oscillator strength an order of magnitude larger than B. The absorption intensity is very sensitive to the position of the first water molecule, as is the wavelength of the transition.
Shemesh, et al. presented a position for the first water molecule similar to that shown in Figure 6b, although not with the twist in pyruvate. The difference between these geometries for the first water molecule is likely due to the different geometries for pyruvate with no water molecules discussed previously.
The remaining geometries for adding water molecules to pyruvate are shown in Figure 7. The excitation wavelengths and oscillator strengths are found in Tables 7 and 8. The excitation wavelengths in the vacuum for pyruvate decrease with the addition of water until the third molecule is added, at which point the energy increases. We propose that the dihedral angle between the ketonic oxygen and the acid oxygen is important for the excitation energy of pyruvate, both in vacuum and in water. Structure A has a dihedral angle of 124.3◦, while structure B has a dihedral angle of 91.3◦. The more planar geometry in A provides a larger delocalization of the π-system than in structure B. A correlation between the excitation energy and the dihedral angle is also observed for the remaining pyruvate structures as shown in Table 7 and 8. A decrease in the excitation energy between the structures can be linked to an increase in the dihedral angle and hereby a more delocalized π- system.
| Table 7: Summary of excitation wavelengths λ of pyruvate with 1, 2, 3, and 4 water molecules, in vacuum and solvent (water). Calculated with CAM-B3LYP/AVTZ. The dihedral angle is defined to be between 90 and 180 degrees, where 180◦ represents a planar molecule. | ||||
| Medium | # of H2O | λ / nm | Osc. strength | Dihedral ang. ( deg ) |
| vacuum | 0 | 312.2 | 0.0004 | 91.41 |
| 1(A) | 328.2 | 0.0011 | 124.3 | |
| 1(B) | 304.1 | 0.0001 | 91.27 | |
| 2 | 332.6 | 0.0005 | 137.2 | |
| 3 | 315.9 | 0.0013 | 124.1 | |
| 4 | 313.7 | 0.0008 | 124.4 | |
| water | 0 | 295.9 | 0.0005 | 90.07 |
| 1(A) | 330.3 | 0.0004 | 142.3 | |
| 1(B) | 293.5 | 0.0002 | 90.12 | |
| 2 | 340.8 | 0.0001 | 172.3 | |
| 3 | 333.3 | 0.0001 | 165.5 | |
| 4 | 335.5 | 0 | 179.2 | |
| Table 8: Summary of excitation wavelengths λ of pyruvate with 1, 2, 3, and 4 water molecules, in vacuum and solvent (water). Calculated with ωB97X-D/AVTZ. The dihedral angle is defined to be between 90 and 180 degrees, where 180◦ represents a planar molecule. | ||||
| Medium | # of H2O | λ / nm | Osc. strength | Dihedral ang. ( deg ) |
| vacuum | 0 | 315.1 | ##### | 91.37 |
| 1(A) | 323.5 | ##### | 114.8 | |
| 1(B) | 295.4 | ##### | 91.39 | |
| 2 | 322 | ##### | 121.8 | |
| 3 | 301.6 | ##### | 95.92 | |
| 4 | 301.3 | ##### | 94.97 | |
| water | 0 | 298.7 | ##### | 90.14 |
| 1∗(A) | 310.2 | ##### | 116 | |
| 2 | 334.8 | ##### | 150.6 | |
| 3 | 290.1 | ##### | 90.51 | |
| 4 | 294.3 | ##### | 94.9 | |
| ∗ We were not able to optimize structure B in water. | ||||
Neither in vacuum nor in a solvent, is a trend observed for the oscillator strengths when more water molecules are added. Therefore, it is difficult to conclude anything about how the probability of the excitation of pyruvate changes when the molecule is hydrated. However, compared to the neutral ketones, which showed very low oscillator strengths, it is easier to differentiate between the magnitudes of the transitions of pyruvate due to the somewhat larger oscillator strengths.
A large disagreement is found in comparing the excitation energies shown here with the literature values by Shemesh, et al. [17]; a difference of 74.9 and 77.8 nm is seen between the literature value with the cc-pVDZ basis set and the ωB97X-D and CAM-B3LYP values, respectively. These variations in excitation wavelength are larger than could be explained as arising from the choice of method. As discussed previously we find a geometry for pyruvate that is different from that of Shemesh, et al. It is expected that a flat molecule (as calculated by Shemesh, et al.) has a larger delocalization of the pi-system than that of a molecule with the methyl group twisted away from the rest of the molecule (as found here).
A large difference in excitation wavelength remains when comparing excitation energies, also when adding additional water molecules (Table 9).
| Table 9: Comparison of the addition of water molecules to pyruvate, in vacuum. The values from this study were calculated using the TD-SCF method, with the given functional and the aug-cc-pVTZ basis set. | ||||
| # H2O | λ / nm | Osc. strength | Method | Ref |
| 0 | 390 | 6.38E-06 | ADC(2)/cc-pVDZ | [17] |
| 312 | 0.0004 | CAM-B3LYP | this work | |
| 315 | 0.0005 | ωB97X-D | this work | |
| 1 | 372 | 6.5E-07 | ADC(2)/cc-pVDZ | [17] |
| 328 | 0.0011 | CAM-B3LYP | this work | |
| 324 | 0.0013 | ωB97X-D | this work | |
| 2 | 371 | 9E-08 | ADC(2)/cc-pVDZ | [17] |
| 333 | 0.0005 | CAM-B3LYP | this work | |
| 322 | 0.0007 | ωB97X-D | this work | |
| 3 | 349 | 0.0005033 | ADC(2)/cc-pVDZ | [17] |
| 316 | 0.0013 | CAM-B3LYP | this work | |
| 302 | 0.0013 | ωB97X-D | this work | |
| 4 | 331 | 0.0004067 | ADC(2)/cc-pVDZ | [17] |
| 314 | 0.0008 | CAM-B3LYP | this work | |
| 301 | 0.0001 | ωB97X-D | this work | |
The largest disagreement between this study and Shemesh, et al. is in systems with no surrounding water molecules. Adding water to the structure, the differences become smaller. In the work by Shemesh, et al. adding the third and fourth water molecules results in a ”twist” in the geometry of pyruvate. One could argue that since this twist is seen for all calculations for pyruvate in this study, the structures for the third and fourth water molecules are more similar than the remaining structures.
Water cluster: We were unable to optimize pyruvate on the surface of the water cluster with either DFT method. Further calculations are needed to 260 obtain more knowledge on how pyruvate will interact with the cluster.
A summary of the excitation wavelengths and oscillator strengths, calculated with ωB97X-D/AVTZ, is shown in Table 10. These values show that the Tt and Tc conformers of pyruvic acid differ in excitation energy by 11.8 nm in vacuum and 8.9 nm in water (with 0 H2O molecules), with the Tt conformer having the lowest energies. There is an increase in the excitation energy in vacuum from 0 to 4 H2O molecules, observed for both pyruvic acid conformers and pyruvate. The same effect is observed by adding 0 to 4 H2O molecules in water. The Tc conformer furthermore shows a blueshift of 1.1 to 2.4 nm between 4 H2O molecules in vacuum to 0 H2O molecules in water, whereas the Tt conformer shows a redshift of 13.6 to 19.3 nm between the same two structures. This illustrates that the two conformers are differently affected by explicit solvent interactions and the applied solvent model. The energies for the pyruvic acid conformers near the water cluster show excitation energies close to those in a vacuum with 0 individual water molecules.
| Table 10: Summary of pyruvic acid. The number of individual water molecules is given in parentheses. Calculated with ωB97X-D/AVTZ. The energies for the molecules near the cluster presented in this table are those with the lowest energy. | |||
| Medium | Species | Energy (nm) | Osc. strength |
| gas-phase/exp [22] | Pyruvic acid | 350 | - |
| water/exp [17] | Pyruvic acid/Pyruvate | ∼320 | - |
| vacuum (0) | PA Tc PA Tt |
348.8 357.0 |
0.0000 0.0000 |
| Pyruvate | 315.1 | 0.0005 | |
| vacuum (4) | PA Tc PA Tt |
342.4 336.1 |
0.0001 0.0001 |
| Pyruvate | 301.3 | 0.0001 | |
| cluster | PA Tc | 351.6 | 0.0000 |
| PA Tt | 359.8 | 0.0001 | |
| water (0) | PA Tc PA Tt |
340.0 348.9 |
0.0001 0.0001 |
| Pyruvate | 298.7 | 0.0006 | |
| water (4) | PA Tc PA Tt |
337.2 329.6 |
0.0001 0.0001 |
| Pyruvate | 294.3 | 0.0001 | |
Experimental spectra recorded by [17] show that the absorption maxima of pyruvic acid and pyruvate differ by only a few nm in aqueous solution which may indicate the solvation model used in this study is not able to representsent the conformational complexity of the bulk solution. The experimental findings of [17] that the absorption peak of pyruvic acid is blue-shifted by solvation in water is reproduced by our results. Adding solvent molecules to explicitly model the solvent interactions increases the blueshift for solvation in water, showing that incorporating explicit solvent interactions is important for theoretical models.
As expected the Tc conformer shows excitation values closest to the experimental value for pyruvic acid in the gas phase. This was expected as the Tc conformer is the most stable of the neutral ketones.
The addition of water molecules to the different conformers of pyruvic acids tends to increase the excitation energy. This is likely due to the greater stabilization of the ground states relative to the excited states of the molecule when surrounded by an electric field. Furthermore, we generally see a stabilization of the ground state, when individual water molecules are added.
This trend is very clear for the neutral ketones, though not as clear for pyruvate, probably due to its negative charge. It was observed for pyruvate that the dihedral angle of ketonic oxygen and acid oxygen is important for the excitation of the compound. The more planar the molecule is, the more the π-system is delocalized through the molecule. When the dihedral angle increases from adding a water molecule, a blue shift is observed. The presented approach is limited by the number of water molecules included in the molecular cluster. This aspect should be addressed in future work. One approach for including the effects of increasing the number of water molecules is to perform quantum mechanical molecular dynamics calculations where the water molecules far from the organic acid are treated by 304 molecular mechanics [24,25].
We have performed calculations of the excitation wavelengths and oscillator strengths were calculated using B97X-D/AVTZ for the Tt and Tc conformers of pyruvic acid. We have considered how the conformers differ in excitation energy in vacuum and water, as well as the impact of adding water molecules on the excitation energy. The interaction of explicit solvent molecules with the conformers is also highlighted. Additionally, the study shows that the Tc conformer aligns closely with experimental values in the gas phase, with emphasizing its stability. The presence of water molecules influences the excitation energy, with a clear trend of ground-state stabilization observed.
Author contributions
Conceptualization: M.S.J. and K. V. M. Methodology: E. A. P.-S., M.F.J., M.S.J. and K. V. M. Investigation: E. A. P.-S., M.F.J., M.S.J. and K. V. M.
Visualization: E. A. P.-S., M.F.J. Supervision: M.S.J. and K. V. M. Writing—original draft: E. A. P.-S., M.F.J., M.S.J. and K. V. M. Writing—review and editing: E. A. P.-S., M.F.J., M.S.J. and K. V. M.
Data and materials availability: All data needed to evaluate the conclusions can be obtained by e-mail to [email protected]
- George C, Ammann M, D’Anna B, Donaldson D, Nizkorodov SA. Heterogeneous photochemistry in the atmosphere. Chem Rev. 2015;115(10):4218-58. Available from: https://doi.org/10.1021/cr500648z
- Ciuraru R, Fine L, Van Pinxteren M, D’Anna B, Herrmann H, George C. Photosensitized production of functionalized and unsaturated organic compounds at the air-sea interface. Sci Rep. 2015;5:1-10. Available from: https://doi.org/10.1038/srep12741
- Gordon BP, Moore FG, Scatena LF, Richmond GL. On the rise: Experimental and computational vibrational sum frequency spectroscopy studies of pyruvic acid and its surface-active oligomer species at the air-water interface. J Phys Chem A. 2019;123(49):10609-19. Available from: https://doi.org/10.1021/acs.jpca.9b08854
- Anglada JM, Martins-Costa MT, Francisco JS, Ruiz-López MF. Photoinduced oxidation reactions at the air-water interface. J Am Chem Soc. 2020;142(38):16140-55. Available from: https://doi.org/10.1021/jacs.0c06858
- Horowitz A, Meller R, Moortgat GK. The uv–vis absorption cross sections of the α-dicarbonyl compounds: pyruvic acid, biacetyl, and glyoxal. J Photochem Photobiol A Chem. 2001;146(52):19-27. Available from: https://doi.org/10.1016/S1010-6030(01)00601-3
- Mellouki A, Mu Y. On the atmospheric degradation of pyruvic acid in the gas phase. J Photochem Photobiol A Chem. 2003;157(2-3):295-300. Available from: https://doi.org/10.1016/S1010-6030(03)00070-4
- Keller-Rudek H, Moortgat G, Sander R, Sörensen R. The mpi-mainz UV/vis spectral atlas of gaseous molecules of atmospheric interest. Earth Syst Sci Data. 2013;5(2):365-73. Available from: https://doi.org/10.5194/essd-5-365-2013
- Burkholder J, Sander S, Abbatt J, Barker J, Cappa C, Crounse J, et al. Chemical kinetics and photochemical data for use in atmospheric studies; evaluation number 19. Tech. rep., Pasadena, CA: Jet Propulsion Laboratory, National Aeronautics and Space Administration. Available from: https://www.researchgate.net/profile/Robert-Huie/publication/343224193_NASA-JPL_Evaluation_19-5/links/5f1de1e192851cd5fa4b0cef/NASA-JPL-Evaluation-19-5.pdf
- Blair SL, Reed Harris AE, Frandsen BN, Kjaergaard HG, Panguí E, Cazaunau M, et al. Conformer-specific photolysis of pyruvic acid and the effect of water. J Phys Chem A. 2020;124(7):1240-52. Available from:https://doi.org/10.1021/acs.jpca.9b10613
- Chai JD, Head-Gordon M. Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections. Phys Chem Chem Phys. 2008;10:6615-20. Available from: https://doi.org/10.1039/b810189b
- Yanai T, Tew D, Handy N. A new hybrid exchange-correlation functional using the coulomb-attenuating method (cam-b3lyp). Chem Phys Lett. 2004;393:51-7. Available from: https://doi.org/10.1016/j.cplett.2004.06.011
- Dunning Jr TH. Gaussian basis sets for use in correlated molecular calculations. i. the atoms boron through neon and hydrogen. J Chem Phys. 1989;90:1007-23. Available from: https://doi.org/10.1063/1.456153
- Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, et al. Gaussian 16 Revision C.01. Wallingford CT: Gaussian Inc.; 2016.
- Rosati B, Christiansen S, Wollesen de Jonge R, Roldin P, Jensen MM, Wang K, et al. New particle formation and growth from dimethyl sulfide oxidation by hydroxyl radicals. ACS Earth Space Chem. 2021;5(4):801-811. PMID: 33889792. Available from: https://doi.org/10.1021/acsearthspacechem.0c00333
- Kubečka J, Christensen AS, Rasmussen FR, Elm J. Quantum machine learning approach for studying atmospheric cluster formation. Environ Sci Technol Lett. 2022;9(3):239-44. Available from: https://doi.org/10.1021/acs.estlett.1c00997
- Elm J, Bilde M, Mikkelsen KV. Assessment of density functional theory in predicting structures and free energies of reaction of atmospheric prenucleation clusters. J Chem Theory Comput. 2012 Jun 12;8(6):2071-7. Available from: https://doi.org/10.1021/ct300192p.
- Shemesh D, Luo M, Grassian V, Gerber RB. Absorption spectra of pyruvic acid in water: Insights from calculations for small hydrates and comparison to experiment. Phys Chem Chem Phys. 2020;22. Available from: https://pubs.rsc.org/en/content/articlelanding/2020/cp/d0cp01810d
- Kakkar R, Chadha P, Verma D. A theoretical study of structures and unimolecular decomposition pathways of pyruvic acid. Internet Electron J Mol Des. 2006;5(1):27-48. Available from: https://www.researchgate.net/publication/228504770_A_Theoretical_Study_of_Structures_and_Unimolecular_Decomposition_Pathways_of_Pyruvic_Acid
- Bartlett RJ, Musiał M. Coupled-cluster theory in quantum chemistry. Rev Mod Phys. 2007;79(1):291. Available from: https://doi.org/10.1103/RevModPhys.79.291
- Suellen C, Freitas RG, Loos PF, Jacquemin D. Cross-comparisons between experiment, td-dft, cc, and adc for transition energies. J Chem Theory Comput. 2019;15(8):4581-90. Available from: https://doi.org/10.1021/acs.jctc.9b00446
- Chang XP, Fang Q, Cui G. Mechanistic photodecarboxylation of pyruvic acid: Excited-state proton transfer and three-state intersection. J Chem Phys. 2014;141(15):154311. Available from: https://doi.org/10.1063/1.4898085
- Yamamoto S, Back R. The photolysis and thermal decomposition of pyruvic acid in the gas phase. Can J Chem. 1985;63(2):549-54. Available from: https://www.semanticscholar.org/paper/The-photolysis-and-thermal-decomposition-of-pyruvic-Yamamoto-Back/5305af9df854c6ff82958d02617d182b86ba181a
- Jensen F. Introduction to Computational Chemistry. Germany: Wiley; 2017.
- Hillers-Bendtsen AE, Todarwal Y, Pittelkow M, Norman P, Mikkelsen KV. Modeling absorption and emission spectroscopies of symmetric and asymmetric azaoxahelicenes in vacuum and solution. J Phys Chem A. 2022;126(37):6467-72. Available from: https://doi.org/10.1021/acs.jpca.2c05721
- Hillers-Bendtsen AE, Todarwal Y, Norman P, Mikkelsen KV. Dynamical effects of solvation on norbornadiene/quadricyclane systems. J Phys Chem A. 2024;128(13):2602-10. PMID: 38511966. Available from: https://doi.org/10.1021/acs.jpca.4c00045