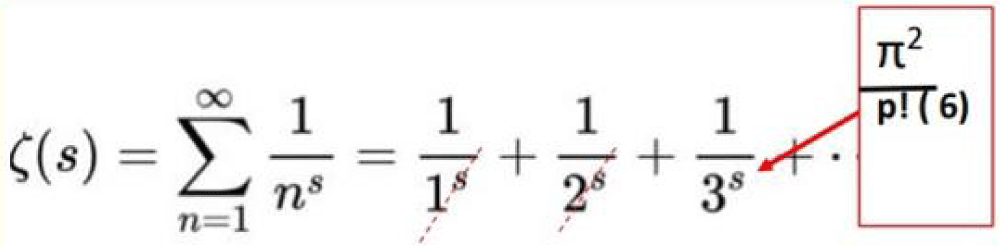Reinterpreting the Riemann Hypothesis: A Theoretical Framework Bridging Mathematics and Universal Symmetry

Mathematics, as a universal language, bridges human perception with the intricate structures of the universe. This study delves into the Riemann Hypothesis, exploring its implications for prime numbers, universal constants, and mathematical physics. Through an interdisciplinary approach involving charge, parity, and time reversal symmetry (CPT symmetry) and universal energy constructs, we propose a novel theoretical framework that reinterprets the Riemann zeta function. This framework sheds light on the symmetry and structural gaps between human mathematical constructs and the natural order, offering pathways toward a comprehensive understanding of the universe.

Our understanding of the universe’s geometry and its governing mathematical laws is often constrained by human perception. For centuries, we have relied on systems like Cartesian coordinates, despite the more universal applicability of polar coordinates and trigonometry. These limitations have shaped our approach to mathematics and its connection to natural events and entities. Central to this exploration are constants like π and i, which serve as the foundation for wave equations, Fourier series, and quantum mechanics. These constants are not merely numbers but represent universal physical phenomena embedded in energy states and atomic spectra. The Riemann Hypothesis, with its intricate connection to prime numbers and universal symmetries, exemplifies the gaps between human mathematical constructs and the universe’s true structure.

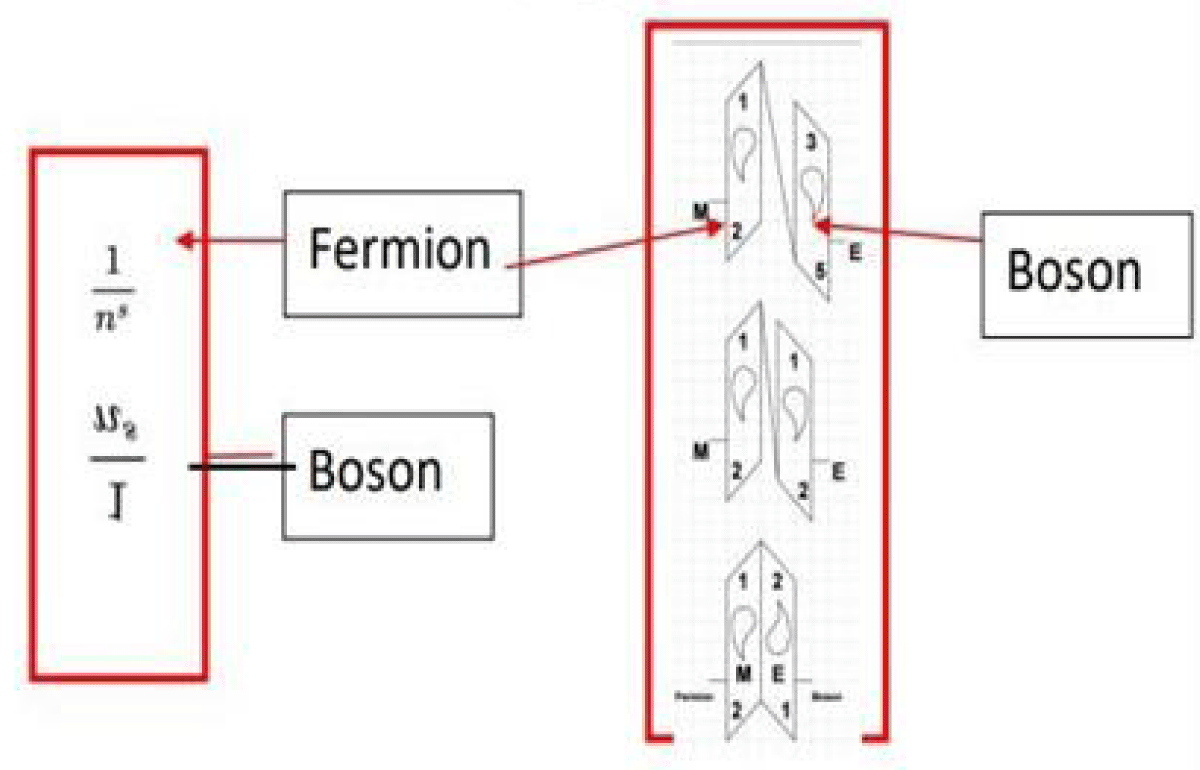
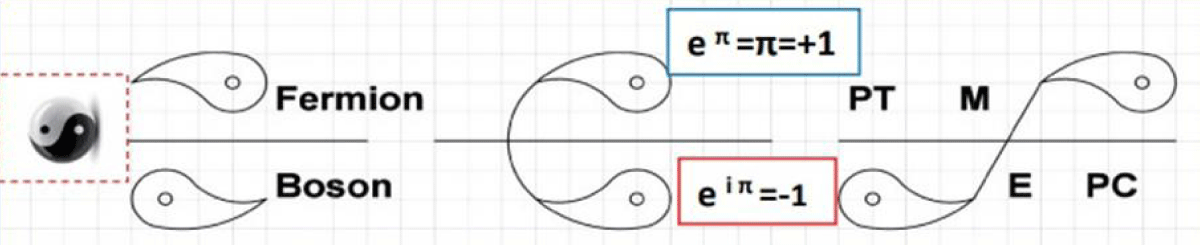
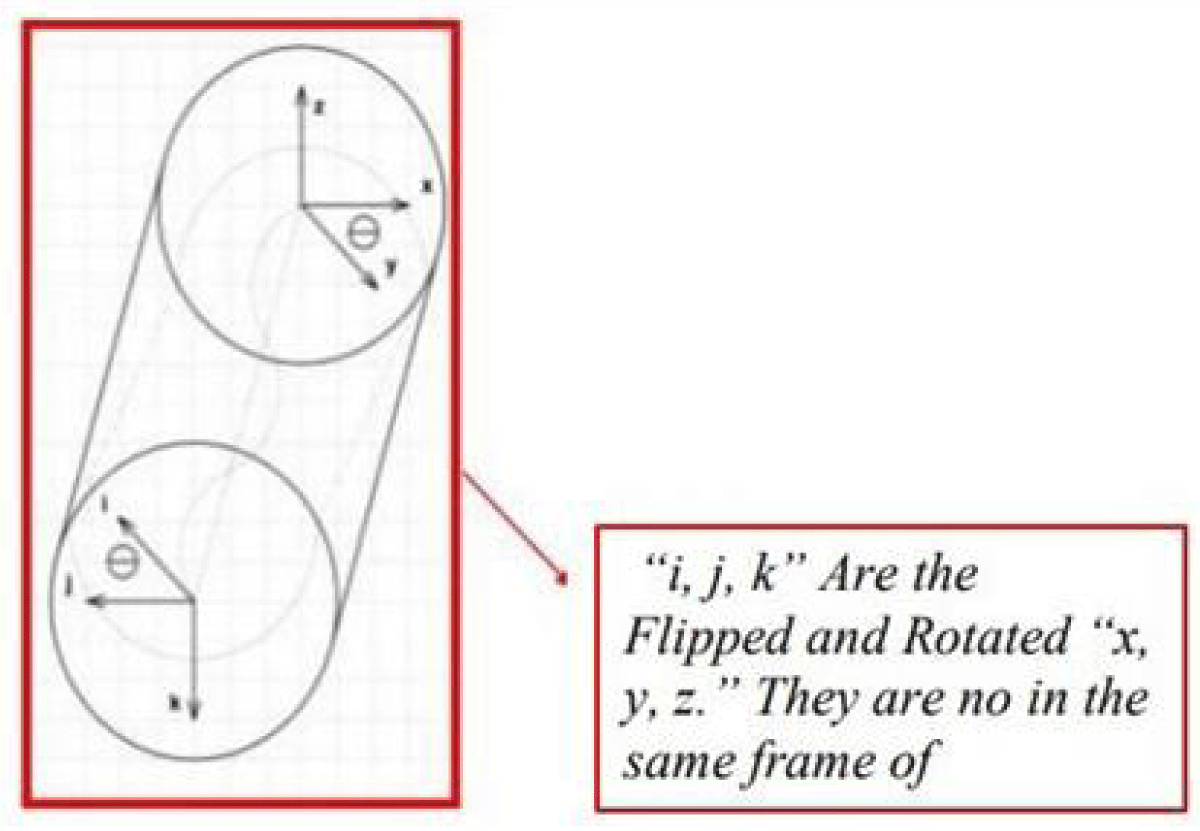
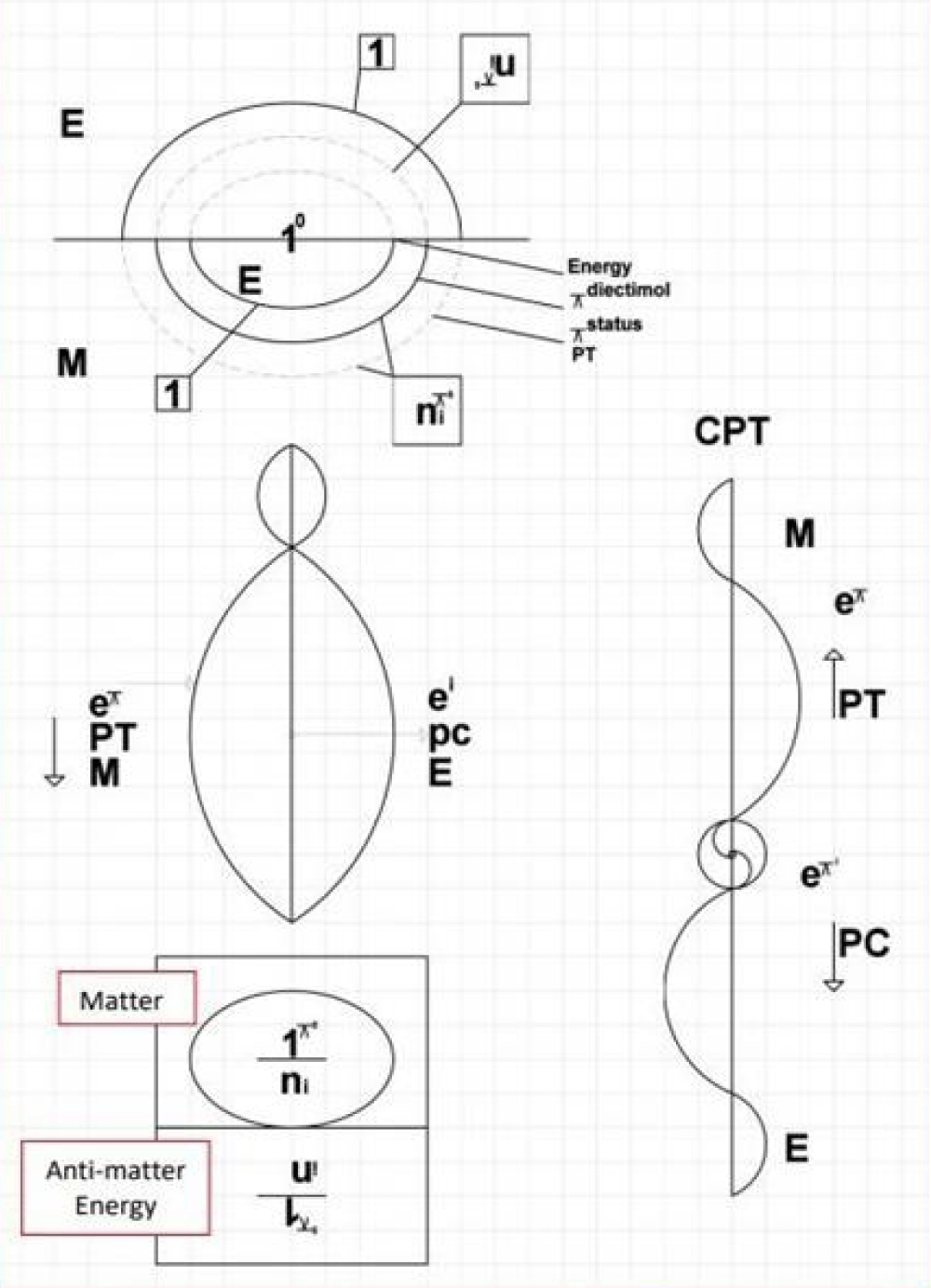
By revisiting the Riemann Hypothesis through the lens of universal “CPT” symmetry breaking, this study proposes a new interpretation that bridges these gaps. Symmetry-breaking phenomena, such as those found in the spontaneous violation of “CPT,” align with the Riemann zeta function’s structural intricacies [1,2] (Figure 1-1, 1-2). Furthermore, the reinterpretation of “i, j, k” in quaternion mathematics and their role in unseen energetic coordinates highlights the hidden complexity of universal mathematics (Figure 1-3). This study challenges traditional notions of imaginary numbers and redefines their significance within the Riemann zeta function. Ultimately, this research aims to connect prime number theory, universal constants, and mathematical physics, providing new pathways for understanding the universe’s energy, matter,

The Riemann Hypothesis, one of the most significant unsolved problems in mathematics, addresses the distribution of prime numbers. Its implications extend beyond number theory, influencing quantum mechanics, cosmology, and the fundamental nature of the universe [3,4]. This study explores the hypothesis through an interdisciplinary lens, integrating universal constants and symmetry principles to propose a holistic understanding of mathematical and physical realities.

Mathematics has been a cornerstone of human civilization, shaping our understanding of the universe and its intricate geometries. Historically, humans developed the Cartesian coordinate system to align with their perception of nature, though the polar coordinate system better reflects universal geometries [5,6]. The limitations of human perception often restrict our ability to grasp the universe's true mathematical structures. For example, concepts like the constant π and trigonometric identities such as sine and cosine embody the fundamental essence of natural phenomena, yet their full implications are often overlooked [7].

The universe’s structure, as revealed through Fourier and Laplace series, Maxwell's equations, and quantum mathematics, inherently involves constants like π, e, and i. These constants are integral to the energy states of matter and atomic spectra. The Riemann Hypothesis provides a mathematical lens to explore these universal constants and their relationships, bridging gaps between abstract mathematical theories and physical realities [8,9].

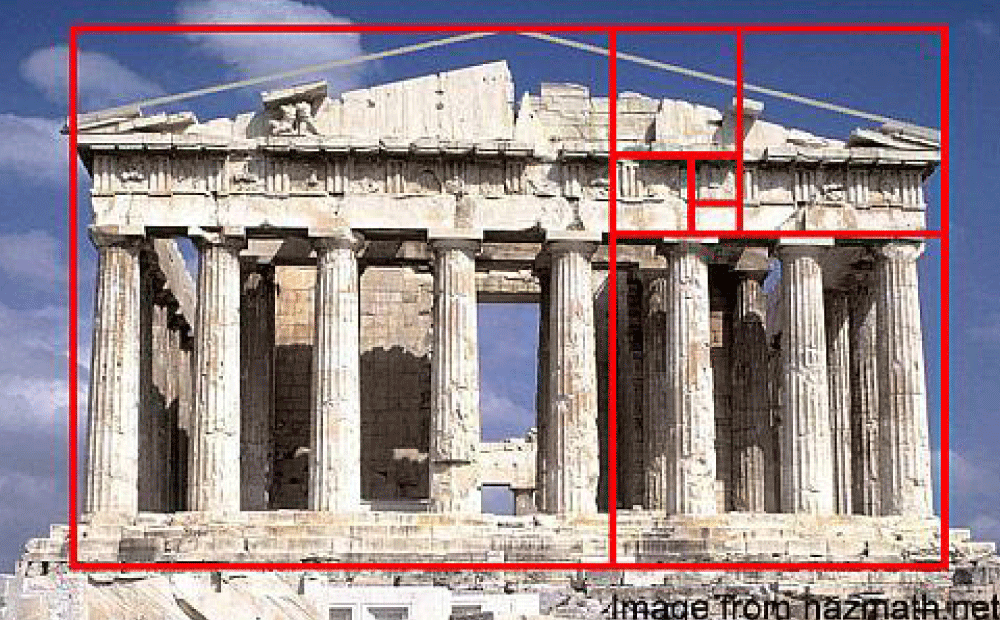
Our understanding of symmetry and geometry also extends to physical constructs, such as the relationship between circles and squares in ancient Egyptian pyramids (Figure 2-1) and the Golden Ratio (Figure 2-2) in Greek architecture. These historical applications illustrate humanity’s attempts to connect mathematical constructs with universal principles [10]. Such insights motivate the exploration of the Riemann Hypothesis in this study, focusing on its potential to unveil hidden symmetries in both mathematics and the natural world.

Moreover, this study integrates the principles of CPT symmetry—spontaneously broken in certain universal contexts—to reinterpret the Riemann Hypothesis. This approach aims to provide a deeper understanding of the interplay between matter and energy configurations, offering a holistic perspective on universal phenomena [11,12].

a) Historical and mathematical foundations

The Riemann Hypothesis, proposed by Bernhard Riemann in 1859, suggests that the non-trivial zeros of the zeta function lie on the critical line with a real part of ½ [1]. This hypothesis has become a central theme in number theory and has profound implications for understanding the distribution of prime numbers. Edwards [4] and Titchmarsh [5] expanded on Riemann's work, exploring the connections between the zeta function and mathematical constructs such as the distribution of prime gaps and the Euler product formula. Ivic [6] and Montgomery [7] further demonstrated the hypothesis's relationship with multiplicative number theory and its applications in modern mathematics.

The zeta function's critical strip and its zeros—both trivial and non-trivial—represent the intricate dance of symmetry and structure in mathematics. Riemann’s insights connected the primes’ unpredictability to a predictable analytical framework, suggesting a universal underlying order. These concepts have driven decades of research and led to modern computational advancements, as noted by Borwein, et al. [8].

b) Interplay of symmetry and mathematics

The symmetry principles inherent in the Riemann Hypothesis and its imaginary side reflect broader patterns in mathematical physics. Conrey [9] noted the role of symmetry in linking the hypothesis to spectral geometry, quantum chaos, and random matrix theory. This connection has fueled interdisciplinary studies bridging pure mathematics with physics and cosmology.

The interplay between symmetry and mathematics is further illuminated by CPT symmetry—a fundamental principle in quantum field theory. The CPT theorem posits that the laws of physics remain invariant under combined transformations of charge conjugation (C), parity (P), and time reversal (T) [11,12] (Figure 3-b1). However, spontaneous symmetry breaking, a phenomenon observed in quantum mechanics and cosmology, reveals underlying asymmetries that parallel the gaps in human mathematical understanding of universal truths [13-16].

c) Universal constants and the nature of mathematics

The mathematical constants π, e, and i represent the foundation of universal geometries and energy constructs. These constants, deeply embedded in the Riemann zeta function, signify the inherent connections between mathematics and the physical universe. Landau and Lifshitz [17] discussed how these constants govern statistical physics and quantum mechanics, while Dirac [18] linked them to the quantization of singularities in electromagnetic fields.

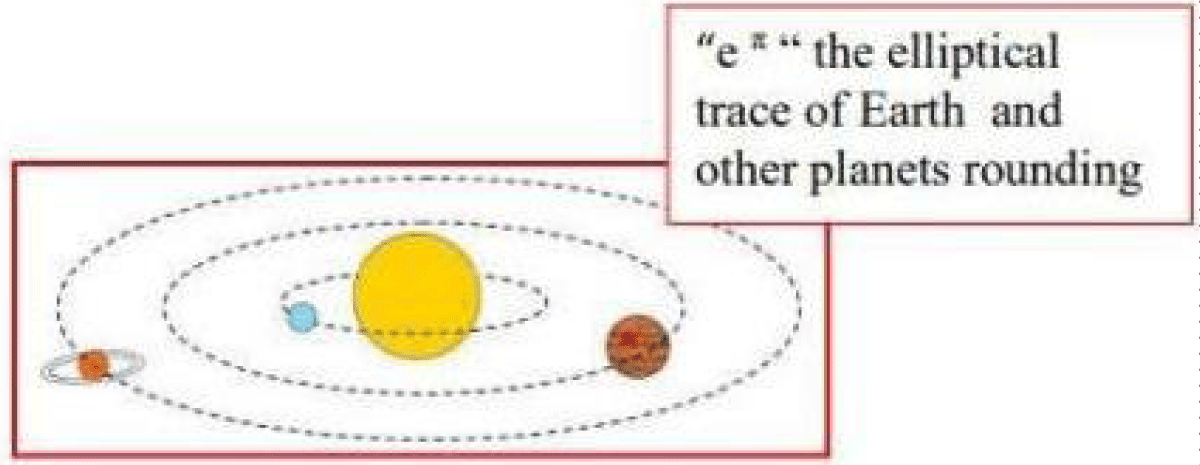
The geometric implications of these constants extend to the elliptical trajectories of celestial bodies (Figure 3-c1) and the structure of atomic spectraEinstein’s field equations [19] and Planck’s quantization principles [20] demonstrate the constants' role in defining the universe’s energetic and material structure. Wheeler and Ford [21] emphasized that these constants are not merely mathematical abstractions but reflect the universe’s inherent order and balance.

d) Challenges in mathematical representation

Human-created numerical systems, particularly the decimal system, often fail to align with the universe’s intrinsic language. The Riemann zeta function’s reliance on natural numbers exemplifies this limitation. By reinterpreting numerical constructs through the lens of symmetry and universal constants, we can bridge the gap between human perception and the universe’s underlying mathematical framework [5,22].

This section provides the groundwork for exploring the proposed theoretical framework, which integrates CPT symmetry, universal constants, and a reimagined Riemann zeta function to uncover deeper truths about mathematics and the cosmos [1,23-25].

a) Revisiting the riemann zeta function

The traditional Riemann zeta function depends on a natural number system that does not fully encapsulate the universe's intrinsic structures. To address this, we propose a modified framework incorporating universal constants, such as π, e, and i, which are integral to understanding the energy and geometries of the cosmos. These constants allow for a reimagined zeta function, embedding elliptical geometries and symmetry-breaking phenomena to align the mathematical model with physical realities [17,18].

By redefining the zeta function to reflect elliptical and higher-dimensional spaces, we incorporate the inherent asymmetry observed in nature. This approach aligns the primes’ distribution with universal constants and their geometric representations, such as circles and ellipses, which dominate celestial and quantum structures [20].

b) Embedding CPT symmetry and its violation

CPT symmetry offers a robust lens to reinterpret the Riemann zeta function. This symmetry ensures that physical laws remain invariant under combined transformations of charge conjugation (C), parity (P), and time reversal (T) [11]. However, the spontaneous breaking of CPT symmetry in certain contexts reveals a fundamental asymmetry that mirrors the gaps in the zeta function’s current interpretation.

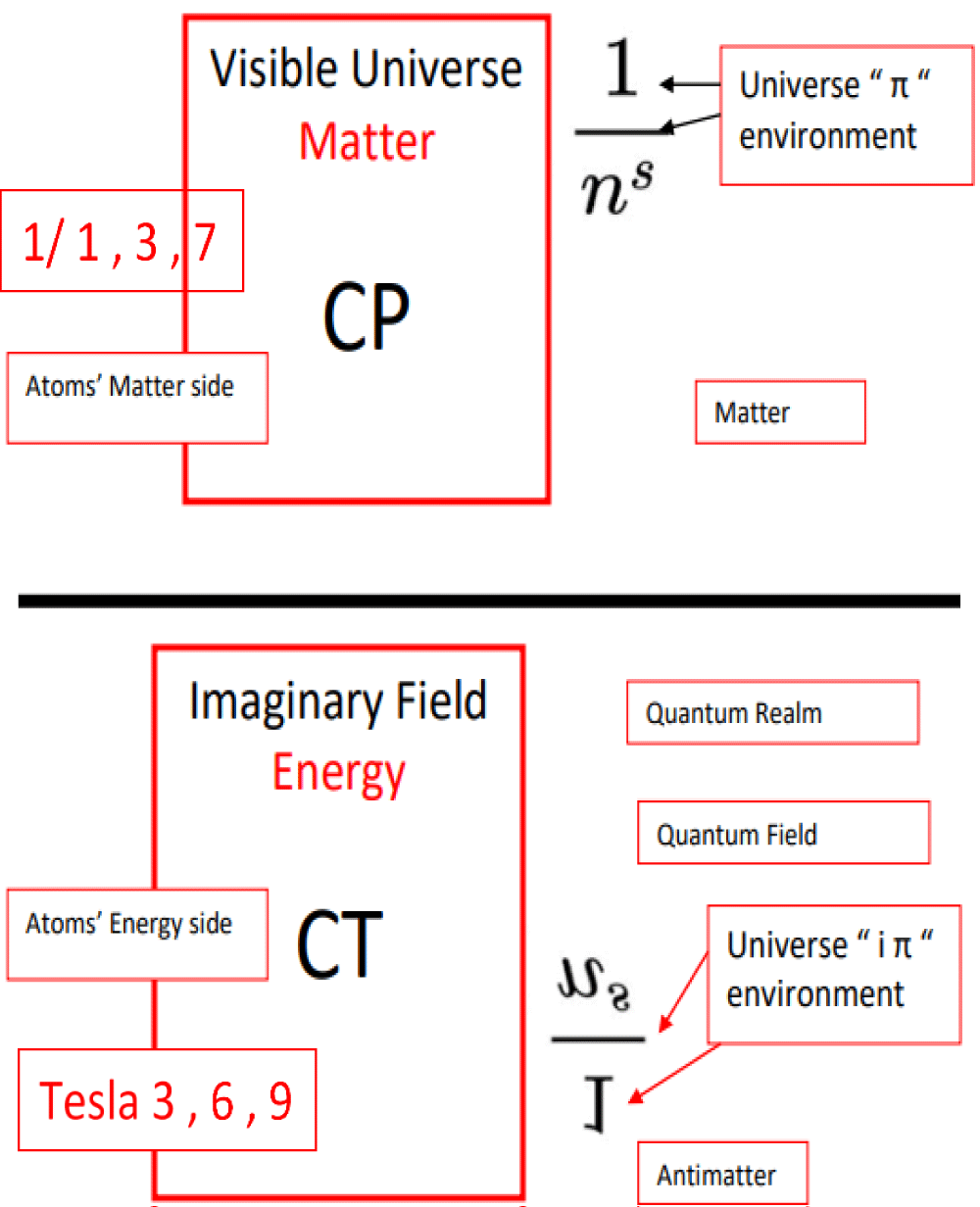
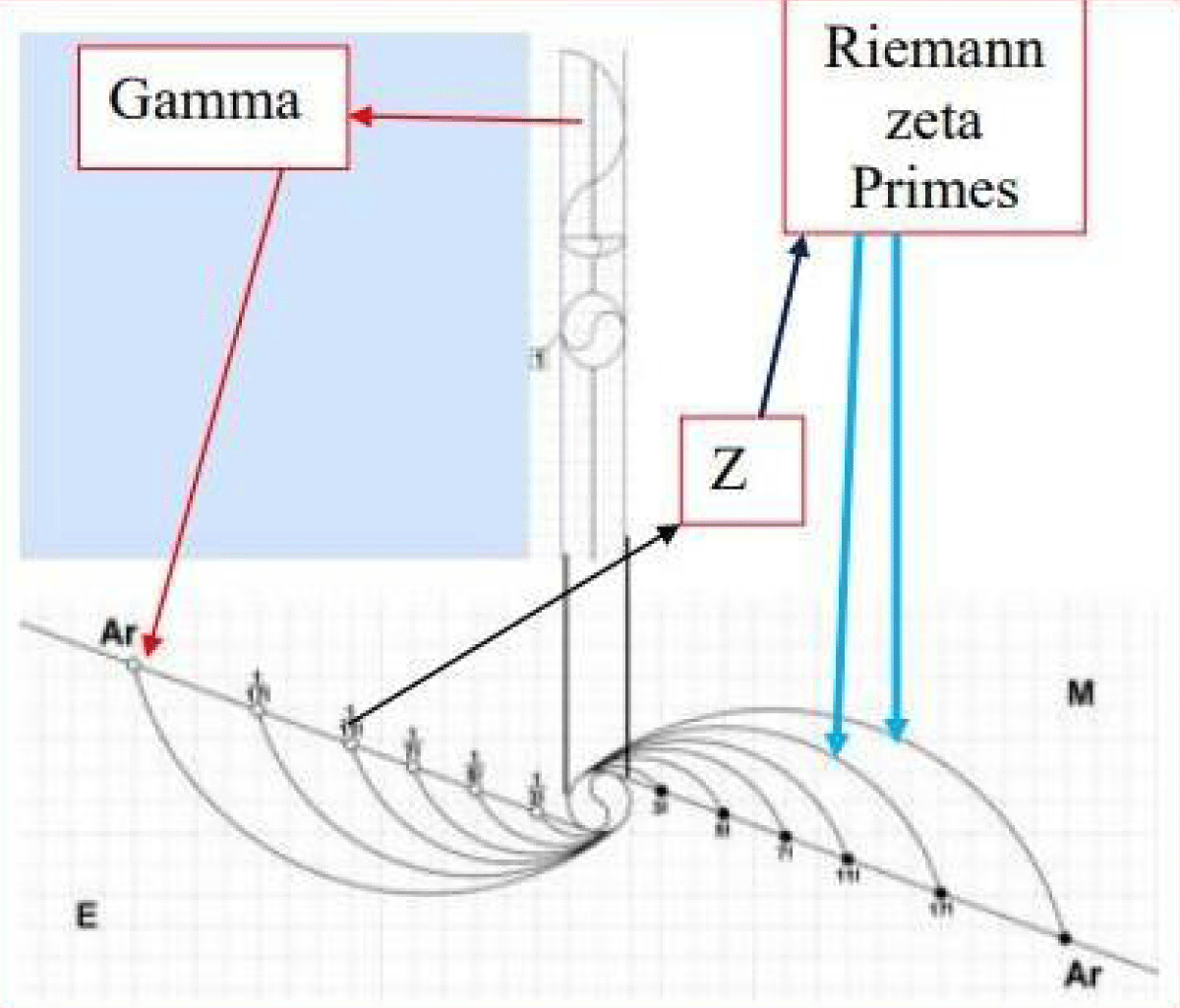
We propose that the Riemann zeta function plays two roles in CPT violation. One is the numerator (“PT”) represents matter configurations, while the other is converted and rotated representing the denominator (“PC”) signifies energetic and anti-matter counterparts [1,2](Figure 4-b1). This bifurcation not only redefines the function but also highlights the dynamic interplay between matter and energy, akin to the dual nature of particles and waves in quantum mechanics [18]. These insights allow for a reimagined prime number distribution as part of a universal energetic framework.

c) Universal constants in energy and matter configurations

Universal constants such as π, e, and i are not arbitrary; they signify fundamental energy and matter interactions within the universe. The role of π, for instance, extends beyond mathematical abstraction to describe the elliptical motion of celestial bodies and the geometry of atomic orbits [20]. Similarly, Euler’s identity (“e^{iπ} + 1 = 0”) encapsulates the harmonic balance of energy states in the universe.

In the proposed framework, the constants guide the reformulation of the zeta function by embedding them into its structure. For instance, the elliptical nature of π aligns with the elliptical geometries found in both atomic structures and planetary orbits, creating a mathematical-physical synergy [21]. Furthermore, the exponential growth of e and the imaginary properties of i reflect the universe’s dynamic expansion and energy superposition states [22] (Figure 4-c1).

d) Linking prime numbers to universal structures

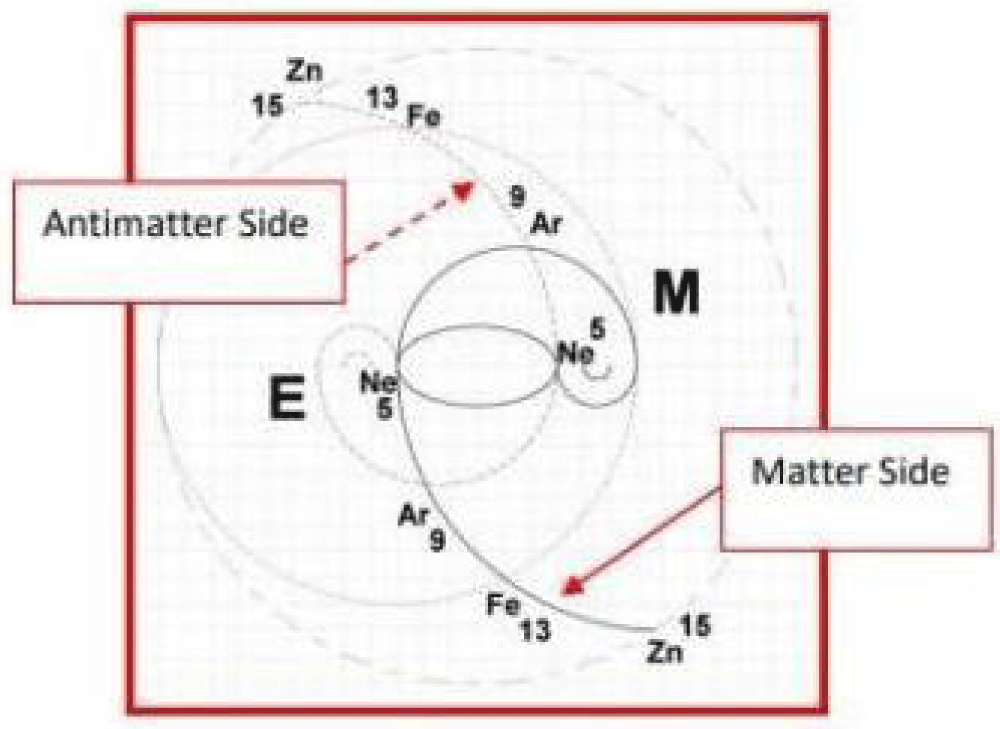
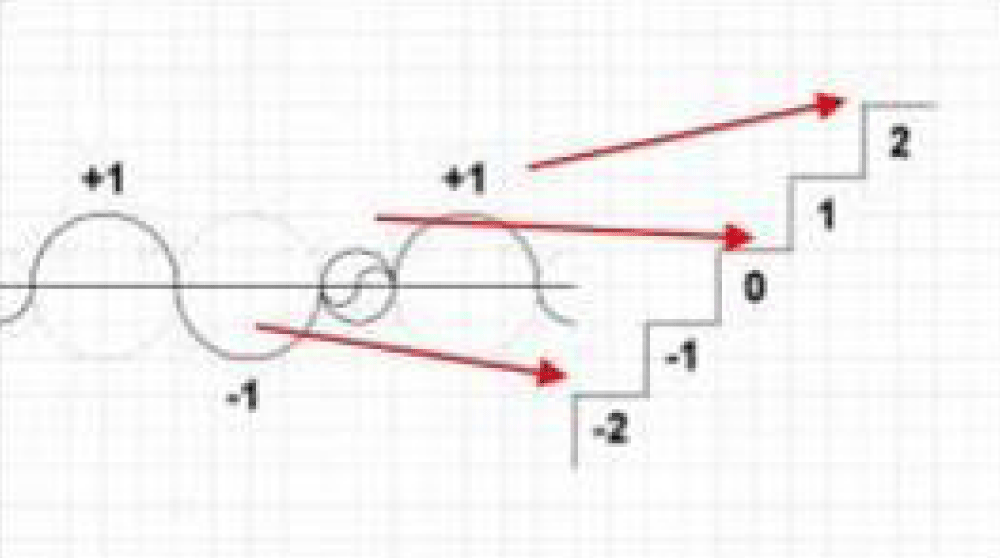
The proposed framework reimagines prime numbers as dynamic entities embedded within the universe’s energetic and geometric constructs. Prime numbers, traditionally treated as discrete entities, are reinterpreted as interconnected points along a continuous wave-like system governed by universal constants [26] (Figure 4-d1). This perspective aligns with the periodicity observed in atomic spectra and the harmonic structures underlying natural phenomena.

The concept of symmetry breaking, essential to CPT violations, also finds resonance in the distribution of prime numbers. By introducing elliptical geometries and redefining the zeta function, we uncover hidden patterns that link primes to universal constants such as π, i, and e. These patterns reflect the balance of symmetry and asymmetry inherent in the universe [27].

e) Visualization and application

Figures and diagrams illustrating the elliptical trajectories, symmetry-breaking phenomena, and universal constants within the zeta function are crucial to this framework (Figure 4-e1). These visual representations provide intuitive insights into the complex interplay between mathematics and physics, paving the way for applications in quantum mechanics, cosmology, and computational number theory [28].

This theoretical framework not only redefines the Riemann zeta function but also integrates it into a broader understanding of the universe’s energetic and geometric principles. By embedding universal constants and CPT symmetry into its structure, this framework bridges gaps between mathematical abstractions and physical realities, offering new pathways for interdisciplinary research.

a) Mathematical implications

The proposed theoretical framework introduces significant advancements in understanding the Riemann zeta function by embedding universal constants and symmetry-breaking phenomena. The integration of π and e redefines the critical strip, aligning it with elliptical geometries and higher-dimensional structures [17,20]. This shift in perspective offers a unified approach to analyzing the distribution of prime numbers, treating them as dynamic elements of a continuous system rather than discrete entities.

This framework also reconciles the apparent gaps between human numerical constructs and the natural order (Table 5-a1). The reliance on natural numbers and their decimal representations in the traditional zeta function has often obscured the deeper connections between primes and universal constants. By replacing these constructs with geometric and energetic analogs, the framework enhances the function’s predictive power and applicability across mathematical and physical domains [22,26].

b) Physical implications

The embedding of CPT symmetry and its violations within the Riemann zeta function highlights the dynamic interplay between matter and energy [2]. The numerator (“PT”) and denominator (“PC”) components of the function reflect the duality of physical existence, akin to the matter-antimatter balance observed in quantum mechanics [11,18]. This perspective aligns the mathematical properties of the zeta function with physical phenomena, offering insights into the universe’s energy distribution and structural symmetry.

The elliptical geometries introduced in the framework also find resonance in celestial mechanics and atomic physics. The trajectories of celestial bodies, governed by π and e, mirror the harmonic structures embedded in the zeta function. This alignment suggests a deeper connection between the universe’s macroscopic and microscopic scales, bridging the gaps between cosmology and quantum mechanics [20,27].

c) Applications in modern science

The reinterpretation of prime numbers as wave-like entities governed by universal constants opens new avenues for scientific exploration. In quantum computing, for instance, the framework’s emphasis on continuity and symmetry could enhance algorithms for prime factorization and cryptography. Similarly, the integration of CPT symmetry into the zeta function provides a robust model for analyzing particle interactions and energy states in quantum field theory [11,28].

In cosmology, the framework’s insights into symmetry-breaking phenomena offer a refined understanding of the universe’s expansion and energy balance. By linking the zeta function to universal constants, the framework provides a mathematical basis for exploring dark energy, gravitational waves, and other frontier topics in physics [21,29] (Figure 5-c1).

d) Bridging mathematics and physics

The proposed framework exemplifies the interdisciplinary potential of the Riemann zeta function. By embedding universal constants and symmetry-breaking phenomena, it bridges the abstract realm of mathematics with the empirical world of physics. This synthesis not only enhances our understanding of prime numbers and their distribution but also offers a unified perspective on the universe’s energetic and geometric principles [28,29].

These interpretations underscore the transformative potential of reimagining the Riemann zeta function as a holistic framework that connects mathematical abstractions with physical realities. The insights gained from this approach pave the way for future research at the intersection of mathematics, physics, and cosmology.

Interdisciplinary implications

The proposed framework demonstrates the transformative potential of embedding mathematical constructs within physical and cosmological contexts. By aligning the Riemann zeta function with universal constants and symmetry-breaking phenomena, this study bridges the theoretical gaps between pure mathematics and applied physics. The reinterpretation of prime numbers as interconnected wave-like entities underscores the interconnectedness of the universe’s mathematical and physical realities [20,27].

This alignment offers valuable insights for interdisciplinary research, particularly in fields such as quantum mechanics, where the dual nature of particles resonates with the duality embedded in the zeta function. The integration of CPT symmetry provides a robust foundation for exploring particle interactions and symmetry-breaking phenomena, while the universal constants anchor the framework in empirical reality [11,22].

Broader implications for mathematics and physics

The framework’s emphasis on universal constants highlights the need to revisit traditional mathematical constructs. By replacing human-centric numerical systems with geometrically and energetically aligned models, this study advances a more natural understanding of the universe’s intrinsic order. This shift has profound implications for the study of prime numbers, suggesting that their distribution is not random but deeply rooted in the universe’s structural symmetry [17,21].

In physics, the framework offers new tools for exploring the universe’s energetic and geometric principles. The elliptical geometries embedded in the zeta function mirror the trajectories of celestial bodies and the structures of atomic spectra, providing a unified perspective on macroscopic and microscopic phenomena. These insights could refine existing models of the universe’s expansion, dark energy, and gravitational waves [20,26,30].

Future directions

This study opens the door for future research at the intersection of mathematics, physics, and cosmology. Potential avenues include:

• Quantum computing: Exploring the role of prime numbers in quantum algorithms and cryptography, leveraging the continuity and symmetry embedded in the proposed framework [28].
• Cosmology: Investigating the zeta function’s implications for dark energy, gravitational waves, and other frontier topics, using its alignment with universal constants as a guiding principle [21,29,31].
• Mathematical physics: Developing computational models that integrate the zeta function’s geometric and energetic constructs with physical phenomena, enhancing our understanding of symmetry-breaking and particle interactions [11,18].

Limitations and challenges

While the proposed framework offers a novel perspective on the Riemann zeta function, it also poses challenges. The reinterpretation of prime numbers as wave-like entities requires a paradigm shift in traditional mathematical thinking, which may face resistance from established schools of thought. Additionally, the integration of CPT symmetry into the zeta function’s framework necessitates further empirical validation, particularly in the context of quantum mechanics and cosmology [11,22].

Despite these challenges, the framework’s interdisciplinary approach offers a promising pathway for advancing our understanding of the universe’s mathematical and physical realities. By bridging the gaps between abstraction and empiricism, this study lays the groundwork for future explorations into the fundamental principles governing the cosmos.

The Riemann Hypothesis has long been a cornerstone of mathematical inquiry, offering profound insights into the distribution of prime numbers and the underlying symmetry of the universe. This study advances the hypothesis by embedding it within a broader framework of universal constants and symmetry-breaking phenomena, bridging the theoretical realms of mathematics and physics.

Through the integration of CPT symmetry and geometric constructs, the proposed framework redefines the Riemann zeta function, aligning it with the universe’s energetic and structural principles. This reinterpretation not only resolves existing gaps in mathematical representation but also unveils new pathways for interdisciplinary research, from quantum mechanics to cosmology [11,18].

The reconceptualization of prime numbers as wave-like entities governed by universal constants underscores their role in the universe’s structural harmony. By aligning the zeta function with physical phenomena, such as elliptical geometries and matter-energy dualities, this study highlights the interconnectedness of macroscopic and microscopic scales [20,28].

Looking forward, the proposed framework opens new avenues for exploration, including applications in quantum computing, cryptography, and cosmological modeling. The emphasis on universal constants as anchors of mathematical and physical reality offers a unified perspective that transcends traditional disciplinary boundaries, paving the way for a holistic understanding of the cosmos [21,28].

In conclusion, the integration of the Riemann Hypothesis with universal constants and CPT symmetry represents a transformative step toward unifying mathematical abstractions with physical realities. This interdisciplinary approach not only enhances our understanding of prime numbers and their distribution but also provides a robust foundation for future explorations into the fundamental principles governing the universe. By bridging the gaps between abstraction and empirical observation, this study contributes to the ongoing quest for a comprehensive theory of everything.

1. Safad H. SUSY Boson and Fermion Rejoinder Most Standard Model, Periodic Table, and DNA Curiousness Yin – Adam Model. Phys Opt Sci. 2023;SRC/JPSOS/222. Available from: https://www.onlinescientificresearch.com/articles/susy-boson-and-fermion-rejoinder-most-standard-model-periodic-table-and-dna-curiousness-ldquoyin-ndash-adam-modelrdquo.pdf
2. Hershberger S. The status of supersymmetry. Symmetry Online Magazine. 2021. Available from: https://www.symmetrymagazine.org/article/the-status-of-supersymmetry?language_content_entity=und
3. Riemann B. Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse. Monatsber Berl Akad. 1859. Available from: https://www.emis.de/classics/Riemann/Zeta.pdf
4. Edwards HM. Riemann's Zeta Function. Dover Publications; 2001. Available from: http://www.stat.ucla.edu/~ywu/Riemann.pdf
5. Titchmarsh EC. The Theory of the Riemann Zeta-Function. Oxford University Press; 1986. Available from: https://sites.math.rutgers.edu/~zeilberg/EM18/TitchmarshZeta.pdf
6. Ivic A. The Riemann Zeta-Function: Theory and Applications. Dover Publications. 2003.
7. Montgomery HL, Vaughan RC. Multiplicative Number Theory I: Classical Theory. Cambridge University Press. 2007. Available from: https://ndl.ethernet.edu.et/bitstream/123456789/23715/1/Hugh%20L.%20Montgomery.pdf
8. Borwein J, et al. The Riemann Hypothesis: A Resource for the Afficionado and Virtuoso Alike. Springer. 2008. Available from: https://www.amazon.in/Riemann-Hypothesis-Resource-Afficionado-Mathematics/dp/0387721258
9. Conrey JB. The Riemann Hypothesis. Notices of the AMS. 2003;50(3):341–353. Available from: https://empslocal.ex.ac.uk/people/staff/mrwatkin/zeta/conreyRH.pdf
10. Bombieri E. Problems of the Millennium: The Riemann Hypothesis. Clay Mathematics Institute. 2000. Available from: https://www.claymath.org/wp-content/uploads/2022/05/riemann.pdf
11. Luders G. Proof of the CPT Theorem. Ann Phys (N Y). 1954;2(1):1–15. Available from: http://dx.doi.org/10.1016/0003-4916(57)90032-5
12. Jost R. The General Theory of Quantized Fields. American Mathematical Society. 1957.
13. Streater RF, Wightman AS. PCT, Spin and Statistics, and All That. Princeton University Press. 1980.
14. Weinberg S. The Quantum Theory of Fields, Vol. 1: Foundations. Cambridge University Press. 1995. Available from: https://doi.org/10.1017/CBO9781139644167
15. Sakurai JJ, Napolitano J. Modern Quantum Mechanics. Pearson. 2017. Available from: https://icourse.club/uploads/files/65fb4c16648d2b93f82fe3271c3381c211f2f532.pdf
16. Peskin ME, Schroeder DV. An Introduction to Quantum Field Theory. Westview Press. 1995.
17. Landau LD, Lifshitz EM. Statistical Physics. Butterworth-Heinemann. 1980. Available from: https://ia902908.us.archive.org/31/items/ost-physics-landaulifshitz-statisticalphysics/LandauLifshitz-StatisticalPhysics.pdf
18. Dirac PAM. Quantised Singularities in the Electromagnetic Field. Proc R Soc Lond A Math Phys Eng Sci. 1931;133(821):60–72. Available from: https://royalsocietypublishing.org/doi/10.1098/rspa.1931.0130
19. Einstein A. The Field Equations of Gravitation. Session of the Royal Prussian Academy of Sciences Berlin. 1915;844–847. Available from: https://www.scirp.org/(S(czeh4tfqyw2orz553k1w0r45))/reference/referencespapers?referenceid=1537594
20. Planck M. On the Law of Distribution of Energy in the Normal Spectrum. Ann Phys. 1901;4(3):553–563. Available from: https://doi.org/10.1002/andp.19013090310
21. Wheeler JA, Ford KW. Geons, Black Holes, and Quantum Foam: A Life in Physics. W.W. Norton & Company. 1998. Available from: https://www.scirp.org/reference/referencespapers?referenceid=2648898
22. Hardy GH, Littlewood JE. Contributions to the Theory of the Riemann Zeta-Function. Proc R Soc Lond. 1914. Available from: https://pracownicy.uksw.edu.pl/mwolf/Hardy_Littlewood%20zeta.pdf
23. Safadi H. Why quantum gravity will not be grasped. J Laser Opt Photonics. 2018;5. Available from: https://www.hilarispublisher.com/conference-abstracts-files/2469-410X-C3-029-009.pdf
24. Safadi HH. SUSY Perceptions Reveal Standard Model Contradictions: Gravity absence, Hierarchy problem, Antimatter Puzzle, Muon g-2 Results, Anti-down Quark domination. J Phys Opt Sci. 2021;SRC/JPSOS/155. Available from: https://www.onlinescientificresearch.com/articles/susy-perceptions-reveal-standard-model-contradictions-gravity-absence-hierarchy-problem-antimatter-puzzle-muon-g2-results-antidown.pdf
25. Siegle E. Why You Should Doubt ‘New Physics’ From The Latest Muon g-2 Results. Forbes. 2021. Available from: https://www.forbes.com/sites/startswithabang/2021/04/08/why-you-should-doubt-new-physics-from-the-latest-muon-g-2-results/
26. Euler L. Variae observationes circa series infinitas. Comment Acad Sci Petropol. 1737. Available from: https://scholarlycommons.pacific.edu/euler-works/72/
27. Hilbert D. Mathematical Problems. Bull Am Math Soc. 1900;8(10):437–479. Available from: https://www.astro.puc.cl/~rparra/tools/PAPERS/hilbert_1900.pdf
28. Atiyah M. Elliptic Operators and Compact Groups. Springer; 1976.
29. Heisenberg W. The Uncertainty Principle. Z Phys. 1927;43(3–4):172–196. Available from: http://dx.doi.org/10.1007/BF01397280
30. Ramanujan S. The Lost Notebook and Other Unpublished Papers. Narosa Publishing House; 1988.
31. Safadi HH. How and Where the Standard Model of Particle Physics Hides Dark Matter. J Phys Opt Sci. 2020;2(1):2 of 3. Available from: https://www.onlinescientificresearch.com/articles/how-and-where-the-standard-model-of-particle-physics-hides-dark-matter.pdf